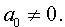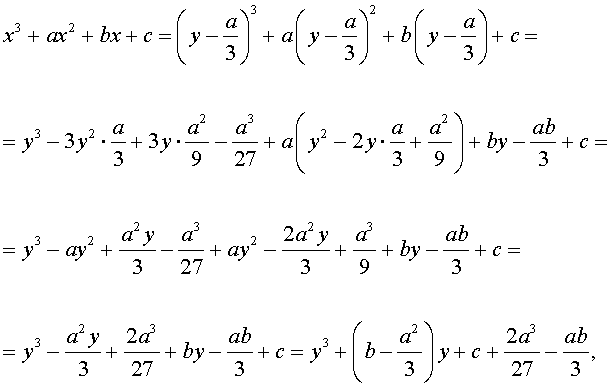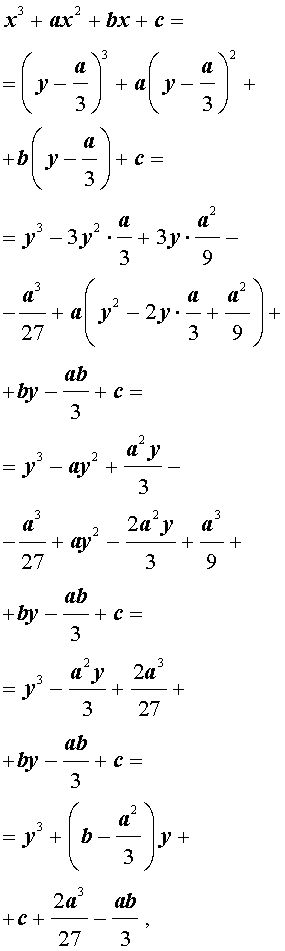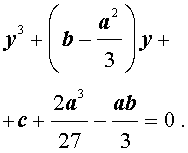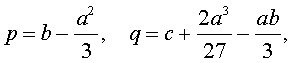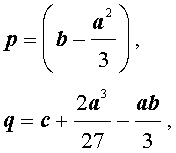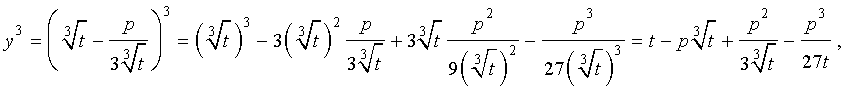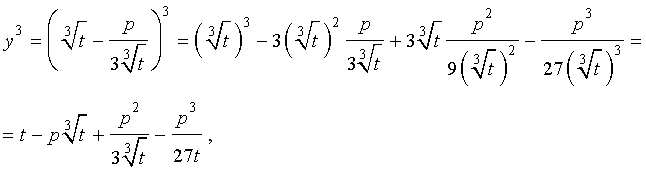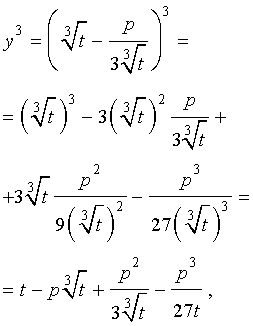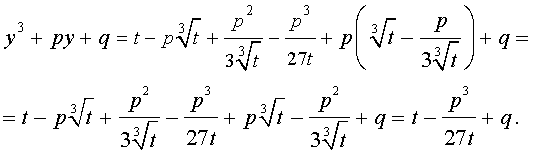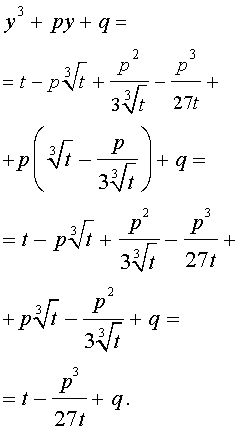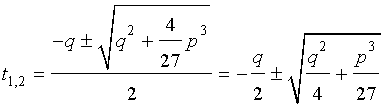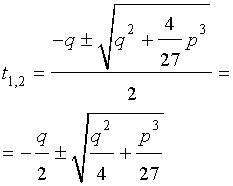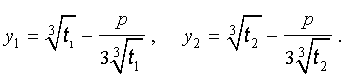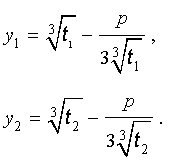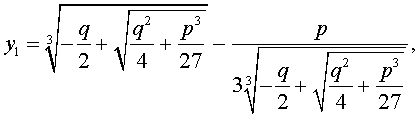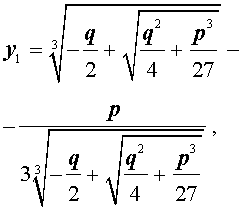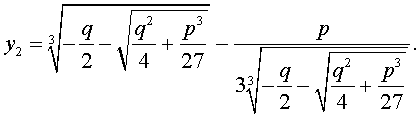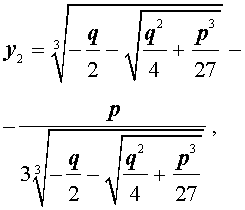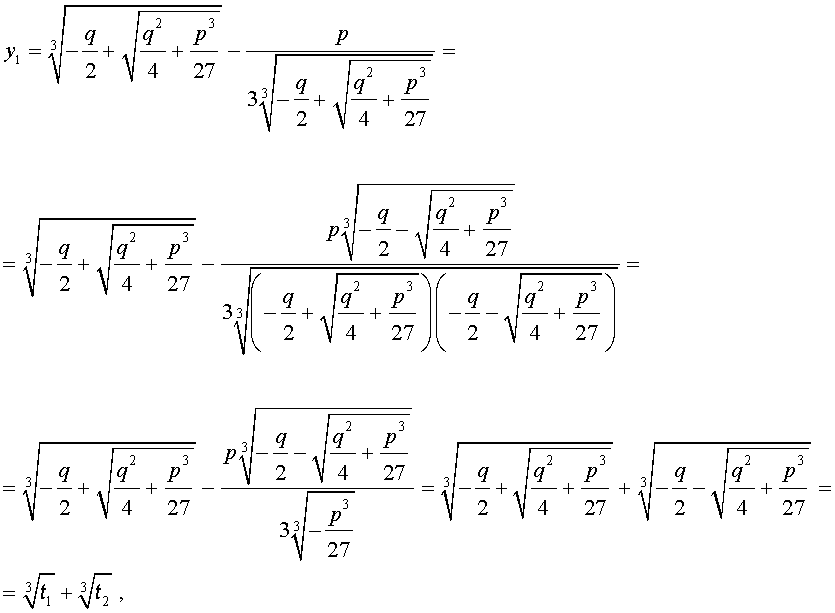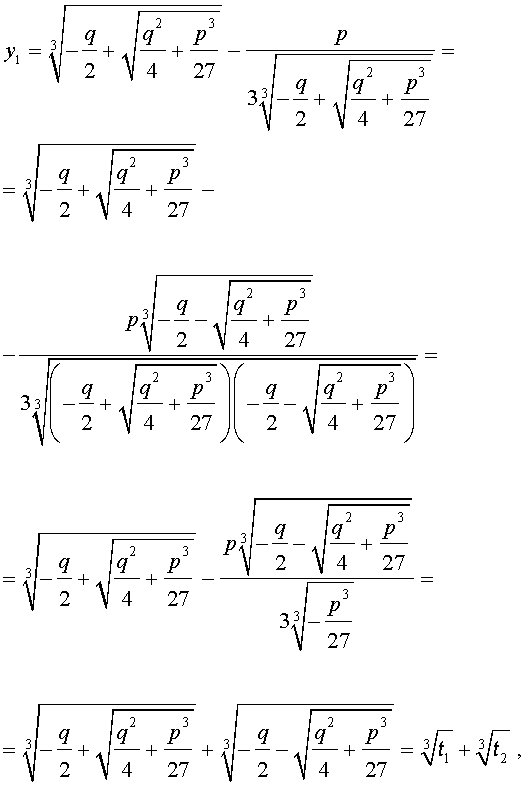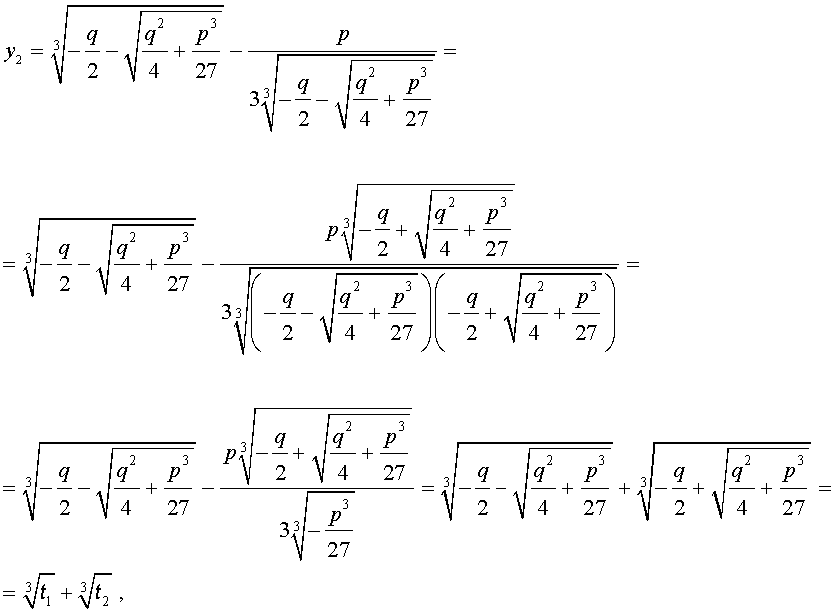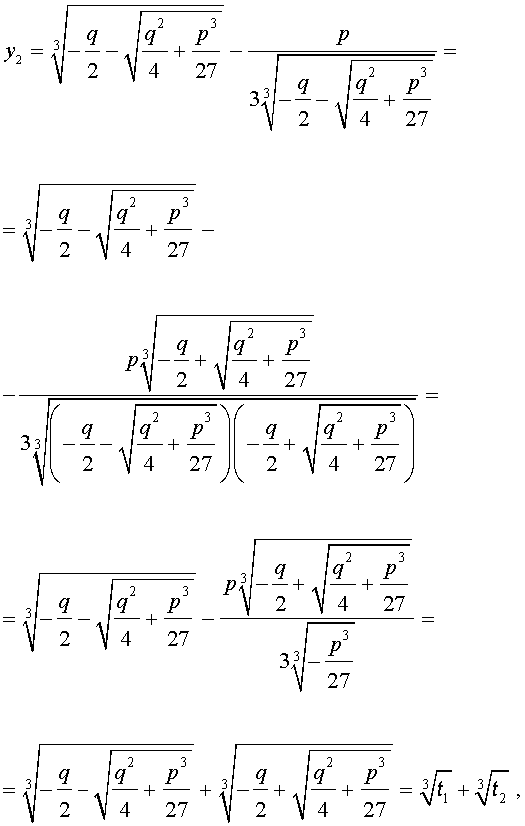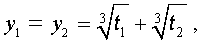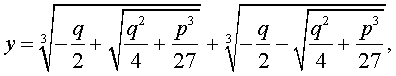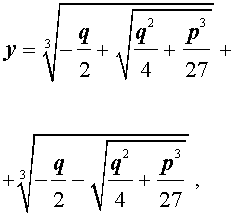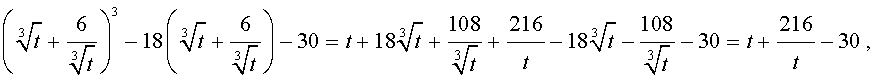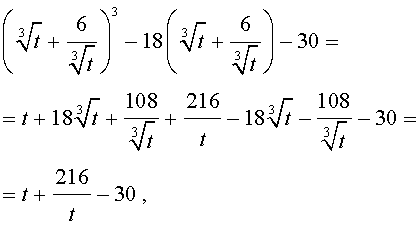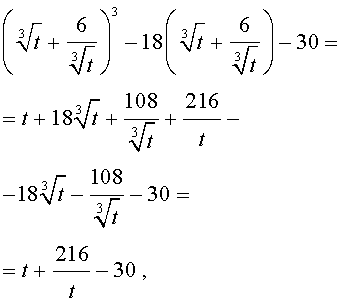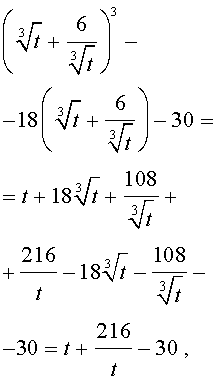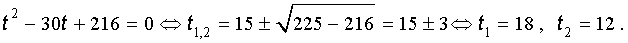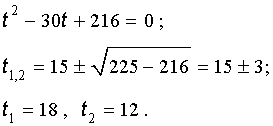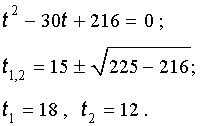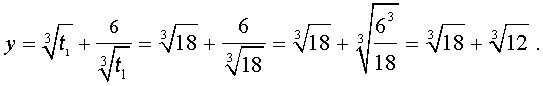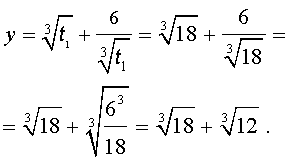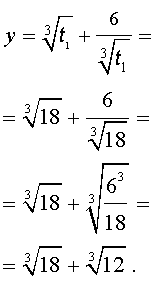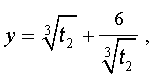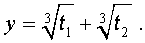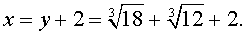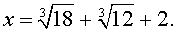Решение кубических уравнений. Формула Кардано
 Схема метода Кардано Схема метода Кардано |
 Приведение кубических уравнений к трехчленному виду Приведение кубических уравнений к трехчленному виду |
 Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
 Формула Кардано Формула Кардано |
 Пример решения кубического уравнения Пример решения кубического уравнения |
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
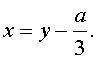 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
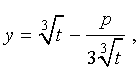 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
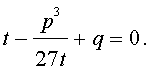 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
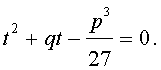 | (8) |
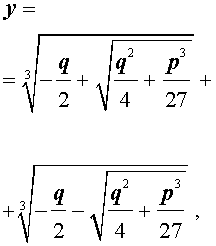
Формула Кардано
Решение уравнения (8) имеет вид:
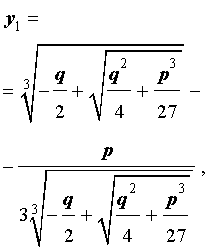
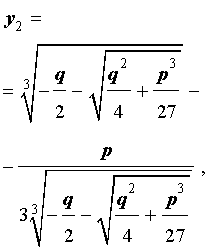
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
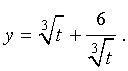 | (16) |
то уравнение (15) примет вид
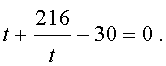 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Вспомогательная страница к разделу ПОЛИНОМ
Решение уравнений в радикалах
Можно ли выразить корни полинома $ f(x)=a_<0>x^n+a_1x^
Задача. Найти выражения корней полинома степени $ n > 2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических операций и операций извлечения корней произвольных (целых) степеней.
Поставленная задача называется задачей о разрешимости уравнения в радикалах 1) .
Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_<>(x)=0 $ делится на старший коэффициент полинома $ f_<>(x) $.
Полином называется нормализованным, если его старший коэффициент равен $ 1_<> $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.
Очевидно, что нормализованный полином имеет те же корни (и в тех же кратностях ), что и исходный. Для простоты обозначений, будем считать, что полином уже нормализован: $$ f(x)=x^n+a_1x^
Второе упрощение заключается в замене переменной (подстановке): $ x=y +\alpha $. Ее результатом будет новый полином той же степени, что и исходный, относительно переменной $ y $: $ F(y)\equiv f(y+\alpha) $. Корни нового полинома связаны (cм. преобразование 2 ☞ ЗДЕСЬ ) с корнями старого по формуле $ \lambda_j = \Lambda_j+\alpha $; так что, найдя корни одного полинома, легко установим и корни другого. Подберем теперь параметр $ \alpha $ так, чтобы обратить в нуль коэффициент при $ y^
Уравнение третьей степени: формула Кардано
Рассмотрим уравнение третьей степени: $$ x^3+p\,x+q=0 $$ Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные $ u_<> $ и $ v_<> $; получим: $$ u^3+v^3+3\,uv(u+v)+p(u+v)+q=0 \ . $$ Сгруппируем: $$ u^3+v^3+(3\,uv+p)(u+v)+q=0 \ . $$ Подчиним теперь неизвестные $ u_<> $ и $ v_<> $ условию $$ 3\,uv+p=0 \ \iff \ uv=-\frac
<3>\ . $$ Тогда предыдущее уравнение приведется к виду $$u^3+v^3=-q \ . $$ Итак, для определения неизвестных величин $ u_<> $ и $ v_<> $ мы получили систему уравнений $$ u^3+v^3=-q,\ uv=-\frac
<3>. $$ Возведя последнее уравнение в куб, получим $$ u^3v^3=-\frac
Выражение $$ \Delta = \frac
Решив квадратное уравнение, получим: $$ u^3=-\frac<2>+ \sqrt<\Delta>,\ v^3=-\frac
<2>— \sqrt <\Delta>\ . $$ В итоге имеем формулу для решений уравнения: $$ x=u+v=\sqrt[3]<-\frac
<2>+\sqrt<\frac
<2>-\sqrt<\frac
Исторические заметки об открытии метода решения кубического уравнения ☞ ЗДЕСЬ.
Формула Кардано не очень удобна для практических вычислений. Дело в том, что корень кубический из комплексного числа принимает три различных значения. Решение же, представленное формулой Кардано, имеет в правой части комбинацию из двух кубических корней. Таким образом, получаем 9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только три решения. Для того, чтобы установить соответствие между значениями $ u_<> $ и $ v_<> $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание значений для $ u_<> $ позволит однозначно восстановить $ v_<> $. Пусть $$ u_1=\sqrt[3]<-\frac<2>+\sqrt<\frac
<3u_1>\ , $$ то решения кубического уравнения можно выразить в виде комбинаций $ u_1 $ и $ v_1 $: $$ \begin
Пример [1]. Решить уравнение $ x^3-6<\mathbf i>\,x^2-10\,x+8 <\mathbf i>=0 $.
Решение. Подстановка $ x=y+2 <\mathbf i>$ приводит уравнение к виду $$y^3+2\,y+4 <\mathbf i>=0 \ , $$ т.е. $ p=2,\,q=4 <\mathbf i>$. Далее $$\Delta=-\frac<100> <27>\ \Rightarrow \ \sqrt <\Delta>= \pm \frac<10 <\mathbf i>><3\sqrt<3>> \ \Rightarrow \ u_1=\sqrt[3]<\left(-2 + \frac<10><3\sqrt<3>> \right)<\mathbf i>> \ . $$ Одно из значений последнего корня: $$u_1=-<\mathbf i>\, \sqrt[3]<-2 + \frac<10><3\sqrt<3>>> \ , $$ это выражение можно упростить, если повезет заметить, что подкоренное выражение равно $ \left(-1+1/<\sqrt<3>>\right)^3 $: $$u_1=<\mathbf i>\left(1-\frac<1><\sqrt<3>>\right)\ \Rightarrow \ v_1=-\frac
<3u_1>= <\mathbf i>\left(1+\frac<1><\sqrt<3>>\right) \ . $$ Получаем: $$\mu_1=2\, <\mathbf i>,\ \mu_2=1- <\mathbf i>,\ \mu_3=-1- <\mathbf i>\ .$$ Значения корней исходного уравнения получатся «сдвигом» на $ 2 <\mathbf i>$.
Анализ формулы Кардано для полиномов с вещественными коэффициентами
Пусть коэффициенты $ p^<> $ и $ q^<> $ уравнения $ x^<3>+p\,x+q=0 $ вещественны. Тогда и дискриминант $$ \Delta = \frac
I. Пусть $ \Delta>0 $. Тогда $ \sqrt <\Delta>$ является числом вещественным, и мы будем считать его положительным. В формуле для $ u_1=\sqrt[3]<-q/2+\sqrt<\Delta>> $ в качестве значения кубического корня возьмем единственное его вещественное значение: $$ u_1 \in \mathbb R \ \Rightarrow \ v_1 \in \mathbb R \ .$$
Согласно формулам $$ \begin
Пример. Решить уравнение $$ x^3-\frac<1> <2>\, x-\frac<1> <2>=0 . $$
Решение. Здесь $$p=-\frac<1><2>,\ q=-\frac<1><2>,\ \Delta=\frac<25><432>,\ u_1=\sqrt[3]<\frac<1><4>+\frac<5 \sqrt<3>><36>> \ , \ v_1=\sqrt[3]<\frac<1><4>-\frac<5 \sqrt<3>><36>> \ . $$ Единственный вещественный корень должен получаться в виде суммы чисел $ u_ <1>$ и $ v_ <1>$ — «сильно» иррациональных, судя по внешнему виду. Тем не менее, этот корень очевиден: $ \lambda = 1 $.
Объяснить эту кажущуюся несуразность можно если заметить, что выражения под кубическими корнями в $ u_ <1>$ и $ v_ <1>$ представимы в виде кубов: $$\frac<1><4>+\frac<5 \sqrt<3>><36>=\left(\frac<1> <2>+\frac<\sqrt<3>> <6>\right)^3 ,\quad \frac<1><4>-\frac<5 \sqrt<3>><36>=\left(\frac<1> <2>-\frac<\sqrt<3>> <6>\right)^3 \ .$$ Тогда и два оставшихся корня $ -1/2 \pm 1/2 \, \mathbf i $ получаются из общих формул. ♦
II. Пусть $ \Delta=0 $. Формулы для корней дают $$ \lambda_1=2 \sqrt[3] <-q/2>\ , \ \lambda_2= \sqrt[3] , \ , \lambda_3= \sqrt[3]
\ , $$ т.е. уравнение имеет кратный корень кратности $ 2_<> $ если $ q\ne 0 $ и кратности $ 3_<> $ если $ q=0 $.
III. Пусть $ \Delta ♦
В только что рассмотренном примере формула Кардано позволяет получить вещественные корни полинома — даже если для их выражения приходится иметь дело с мнимыми числами. Попробуем, однако, применить тот же прием ко следующему примеру.
Пример [2]. Решить уравнение $ x^3-3\,x+1=0 $.
Решение. Здесь $ \Delta=-\frac<3> <4>$ и $ u_1=\sqrt[3]<-\frac<1> <2>+ \frac<\sqrt<3>><2>\, \mathbf i> $. $$\sqrt[3]<-\frac<1> <2>+ \frac<\sqrt<3>><2>\, \mathbf i>= \alpha+ \mathbf i\, \beta \ \Rightarrow \ 4\, \alpha^3-3\, \alpha +\frac<1> <2>=0 \ . $$ Умножив последнее уравнение на $ 2_<> $ и сделав в нем замену переменной $ A = 2\alpha $ мы придем к уравнению $$A^3-3\, A +1 =0 \ , $$ т.е. вернемся к исходному уравнению!
Вывод: все корни полинома вещественны, но в радикалах их можно представить только с помощью мнимых чисел. ♦
Как разрешить этот парадокс?
Как получить вещественный вид для корней полинома? На помощь приходит альтернативный алгебраическому способ извлечения корня кубического из комплексного числа: способ, основанный на представлении этого числа в тригонометрической форме.
Теорема. В случае $ \Delta ♦
Пример. Решить уравнение из предыдущего примера: $ x^3-3\,x+1=0 $.
Решение. Здесь $ p=-3, q=1 $ и $ \displaystyle \varphi = \operatorname
Ответ. $$ 2 \cos \frac<2\pi> <9>\approx 1.53208 \ ,\quad 2 \cos \frac<8\pi> <9>\approx -1.87938\ , \quad 2 \cos \frac <-4\pi> <9>\approx 0.34729 \ . $$ Проверка может быть выполнена применением формулы приведения для степени косинуса, приведенной ☞ ЗДЕСЬ.
Пример. Решить уравнение $ x^3-6\,x+3=0 $.
Решение. Здесь $ p=-6, q=3 $ и $ \displaystyle \varphi = \operatorname
Ответ. $ \approx 2.145103,\ \approx -2.669079,\ \approx 0.523976 $.
Уравнение четвертой степени
рассмотрим в виде: $$ x^4+p\,x^2+q\,x+r=0 , $$ перепишем его в виде $$x^4=-p\,x^2-q\,x-r $$ и прибавим к обеим частям $ x^2t+t^2/4 $, где $ t $ — новая неизвестная: $$ x^4+x^2t+t^2/4=(t-p)\,x^2-q\,x +(t^2/4-r) \ . $$ Левая часть получившегося уравнения является полным квадратом: $$ \left(x^2+t/2 \right)^2 =(t-p)\,x^2-q\,x+(t^2/4-r) \ . $$ Подберем теперь значение $ t $ так, чтобы и правая часть стала полным квадратом.
Теорема. Для того, чтобы квадратный полином $ Ay^2+By+C $ был квадратом полинома первой степени, необходимо и достаточно, чтобы его дискриминант $ B^2-4\,AC $ был равен нулю.
Доказательство. Необходимость. Если $ Ay^2+By+C\equiv (ky+ \ell)^2 $, то $ A=k^2,\, B=2\,k\ell,\, C=\ell^2 $ и тогда очевидно $ B^2-4\,AC=0 $.
Применяя этот результат к правой части полученного уравнения, находим условие на параметр $ t $, при котором это выражение станет полным квадратом: $$ q^2-4\,(t-p)(t^2/4-r)=0\ \iff \ t^3-p\,t^2-4\,r\,t+(4\,pr-q^2)=0 $$ Это уравнение называется резольвентой Феррари для уравнения $ x^4+p\,x^2+q\,x+r=0 $.
Поскольку резольвента Феррари является уравнением кубическим, то его можно разрешить в радикалах по методу изложенному ВЫШЕ. Обозначим через $ t_1 $ какой-то из его корней. При этом значении $ t $ правая часть уравнения $$ \left(x^2+t/2 \right)^2 =(t-p)\,x^2-q\,x+(t^2/4-r) \ . $$ будет полным квадратом: $$ (t_1-p)\,x^2-q\,x+(t_1^2/4-r) \equiv \left(Kx+L \right)^2 \quad npu \quad \ K= \sqrt<2\sqrt
Если обозначить корни этих квадратных уравнений через $ x_1,x_2 $ и, соответственно, $ x_3,x_4 $, то они будут связаны с корнем $ t_ <1>$ резольвенты Феррари равенством $ t_1=x_1x_2+x_3x_4 $. В самом деле, это равенство следует из двух формул Виета: $ x_1x_2=t_1/2-L,\, x_3x_4=t_1/2+L $. Остальные корни резольвенты получаются в результате перестановок $ t_2=x_1x_3+x_2x_4,\, t_3=x_1x_4+x_2x_3 $.
Пример [2]. Решить уравнение $ x^4+4\,x-1=0 $ .
Решение. Здесь $ p=0,\,q=4,r=-1 $ и резольвента Феррари имеет вид $$t^3+4\,t-16=0 \ .$$ Последнее уравнение имеет корень $ t_1=2 $. Следовательно, исходное уравнение можно переписать в виде: $$ (x^2+1)^2 =\left(\sqrt<2>x- \sqrt<2>\right)^2 \ . $$ Оно распадается на два квадратных: $$ x^2+1=\sqrt<2>\, x- \sqrt <2>\ u \ x^2+1=-\sqrt<2>\, x + \sqrt <2>\ . $$
Преобразование Чирнгауза
Успех, достигнутый в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода была очевидна: свести решение уравнения $ n_<> $-й степени к решению уравнения $ (n-1)_<> $-й степени. Одну из возможных вариаций этого подхода поясним на примере.
Пример. Решить уравнение $ x^3+6\,x-2=0 $.
Решение. Обозначим неизвестные корни полинома $ f(x)=x^3+6\,x-2 $ через $ \lambda_1,\lambda_2, \lambda_3 $. Построим полином $ F_<>(y) $, корнями которого являются величины $$ \mu_j=\lambda_j^2+2\, \lambda_j+4 . $$ Выражение $$F(y)= (y-\mu_1)(y-\mu_2)(y-\mu_3)$$ является симметрическим полиномом относительно $ \lambda_1,\lambda_2 $ и $ \lambda_ <3>$. Следовательно, по теореме Гаусса о симметрических полиномах, коэффициенты $ F_<>(y) $ должны полиномиально выражаться через коэффициенты $ f_<>(x) $, т.е. быть числами целыми. Опуская промежуточные выкладки, приведем окончательный результат: $$F(y)\equiv y^3-108 .$$ Корни этого полинома легко определить: $$ \mu_1=3\sqrt[3]<4>,\ \mu_2= 3\sqrt[3] <4>\left(-\frac<1> <2>+\mathbf i \frac<\sqrt<3>> <2>\right),\ \mu_3= 3\sqrt[3]<4>\left(-\frac<1> <2>-\mathbf i \frac<\sqrt<3>> <2>\right) \ . $$ Теперь находим $ \lambda_
Подобное преобразование полинома $ f_<>(x) $ в полином $ F_<>(y) $ той же степени, имеющий корнями числа $ g(\lambda_1),\dots, g(\lambda_n) $ при произвольном полиноме $ g(x)\in \mathbb A[x] $, называется преобразованием Чирнгауза.
Биографические заметки о Чирнгаузе ☞ ЗДЕСЬ.
Задача. Найти такое преобразование Чирнгауза, которое преобразует исходный полином к виду $ y^n-a $. Корни последнего, очевидно, выражаются в радикалах. Если при этом, $ \deg g ♦
Следующий способ нахождения преобразования Чирнгауза является развитием метода Безу вычисления результанта.
Найдем остатки от деления $ x^kg(x) $ на $ f_<>(x) $ $$ g_k(x) = b_
Теорема [Эрмит]. Имеем:
Доказательство. Равенства $$y=g(x),\, xy=g(x)x,\, \dots, x^
Пример. Решить предыдущий пример по методу Эрмита.
Решение. Имеем $$g_0(x)\equiv g(x)=-1+x+x^2, \ g_1(x)=-3+x+x^2, \ g_2(x)=-3-x+x^2 $$ и, следовательно, $$F(y)=(-1)^3\left| \begin
Будем решать теперь вторую из сформулированных выше подзадач: подобрать преобразование Чирнгауза таким образом, чтобы обнулить как можно большее число коэффициентов у полинома $ F_<>(y) $.
Пример. Для полинома $ f(x)=x^3+a_1x^2+a_2x+a_3 \in \mathbb C[x] $ подобрать преобразование Чирнгауза вида $ y=x^2+b_1x+b_2\in \mathbb C[x] $ так, чтобы получившийся в результате преобразования полином имел вид $ F(y)=y^3+c_3 $.
Найти преобразование Чирнгауза, позволяющее решить в радикалах уравнение $ x^3+a_1x^2+\frac<1><3>\, a_1^2x+a_3=0 $.
Статья не закончена!
Разрешимость в радикалах
Успех достигнутый в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода очевидна из предыдущих пунктов: свести решение уравнения $ n_<> $-й степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков мира, решить уравнение пятой степени не удавалось. Наконец, в начале XIX века был получен отрицательный результат.
Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем случае неразрешимо в радикалах.
Пример. Уравнение $ x^5-4\, x -2=0 $ неразрешимо в радикалах.
Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.
Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку $ x^5+x+1\equiv (x^2+x+1)(x^3-x^2+1) $.
Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде формулы, состоящей из конечного набора сравнительно простых функций. Тем не менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти. Cм., к примеру,
Наконец, для практических задач часто более важна не столько «красивая» аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.
Задачи
Источники
[1]. Журавский А.М. Сборник задач по высшей алгебре. М.-Л.ГТТИ. 1933
[2]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
[3]. Калинина Е.А., Утешев А.Ю. Теория исключения: Учеб. пособие. СПб.: НИИ Химии СПбГУ, 2002. 72 с.
http://zaochnik.com/spravochnik/matematika/systems/reshenie-kubicheskih-uravnenij/
http://vmath.ru/vf5/polynomial/radical