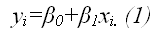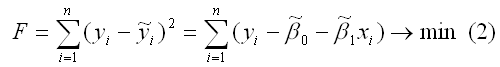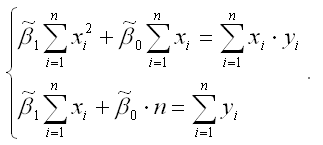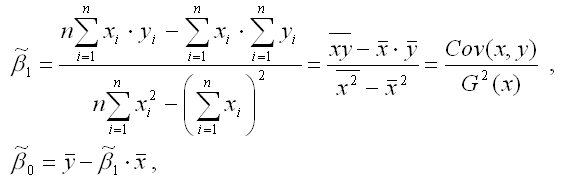Пример решения система нормальных уравнений это

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

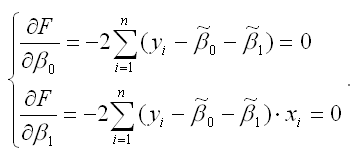
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

23. Нормальные системы линейных однородных дифференциальных

Уравнений с постоянными коэффициентами.

При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется Линейной однородной, если ее можно записать в виде:

(2)

Решения системы (2) обладают следующими свойствами:

Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на Ekx, получаем:

Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т. е.:

В результате вычисления определителя получаем уравнение третьей степени относительно K. Это уравнение называется Характеристическим уравнением И имеет три корня K1, K2, K3. Каждому из этих корней соответствует ненулевое решение системы (2):

Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

Пример. Найти общее решение системы уравнений:

Составим характеристическое уравнение:

Решим систему уравнений:

Для K1:

Полагая (принимается любое значение), получаем:

Для K2:

Полагая (принимается любое значение), получаем:

Общее решение системы:

Этот пример может быть решен другим способом:

Продифференцируем первое уравнение:

Подставим в это выражение производную У¢ =2X + 2Y из второго уравнения.

Подставим сюда У, выраженное из первого уравнения:

Обозначив , получаем решение системы:

Пример. Найти решение системы уравнений

Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т. к. не является однородным (в уравнение входит независимая переменная Х).

Для решения продифференцируем первое уравнение по Х. Получаем:

Заменяя значение Z’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

Пример. Найти решение системы уравнений:

Составим характеристическое уравнение:

Если принять g = 1, то решения в этом случае получаем:

Если принять g = 1, то получаем:

Если принять g = 3, то получаем:

Общее решение имеет вид:

Элементы теории устойчивости.

Теория устойчивости решений дифференциальных уравнений является одним из разделов Качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.

Этот метод особенно важен, т. к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т. е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.

Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

(1)

И начальные условия:

Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.

Теорема. (о непрерывной зависимости решения от начальных условий)

Если правая часть дифференциального уравнения Непрерывна и по переменной у имеет ограниченную частную производную на области прямоугольника, ограниченного , то решение

, удовлетворяющее начальным условиям , непрерывно зависит от начальных данных, т. е. для любого , при котором если

то при условии, что

где

Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.

Определение. Если — решение системы дифференциальных уравнений, то это решение называется Устойчивым по Ляпунову, если для любого , такое, что для любого решения той же системы, начальные условия которого удовлетворяют неравенствам

(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)

Т. е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при T ³ T0.

Если , то решение j(t) называется Асимптотически устойчивым.

Исследование на устойчивость по Ляпунову произвольного решения системы Можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:

(2)

Система (2) имеет тривиальное (равное нулю) решение

Теорема. Решение системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).

Это тривиальное решение называется Положением равновесия Или Точкой покоя.

Определение. Точка покоя Системы (2) устойчива по Ляпунову, если для любого такое, что из неравенства

Теорема. (Теорема Ляпунова). Пусть задана система

Имеющая тривиальное решение .

Пусть существует дифференцируемая функция , удовлетворяющая условиям:

1) ³0 и V = 0 только при у1 = у2 = … = уN =0, т. е. функция V Имеет минимум в начале координат.

2) Полная производная функции V Вдоль фазовой траектории (т. е. вдоль решения Yi(T) системы (1)) удовлетворяет условию:

при

Тогда точка покоя устойчива по Ляпунову.

Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат выполнялось условие

Где B — постоянная величина, то точка покоя асимптотически устойчива.

Функция V называется Функцией Ляпунова.

Классификация точек покоя.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Характеристическое уравнение этой системы имеет вид:

Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя будет устойчива. Такая точка покоя называется Устойчивым узлом.

2) Корни характеристического уравнения действительны и

или .

В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней положителен.

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым седлом.

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым узлом.

Если полученного решения Системы исключить параметр T, то полученная функция дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

b b

Устойчивый узел. Неустойчивый узел. Седло.

5) Корни характеристического уравнения комплексные .

Если Р = 0, т. е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется Центром.

Если P 0, то точка покоя неустойчива и называется Неустойчивым фокусом.

Уравнения математической физики.

Уравнения в частных производных.

Определение. Дифференциальным уравнением в частных производных Называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.

Порядком Дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением Уравнения будет некоторая функция , которая обращает уравнение в тождество.

Методы решения систем линейных нормальных уравнений

Денежки счет любят

(Как Вы уже поняли, геодезия – тоже)

135.1. Способ матричных преобразований

В качестве примера рассмотрим решение системы четырех линейных уравнений матричным способом:

Составим матрицу коэффициентов при х_i , правых частей и контрольного столбца, равного суммам коэффициентов и правой части каждого уравнения по соответствующй строке матрицы:

(14.54)

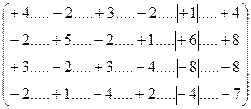
Составление контрольного столбца является обязательным! После математических действий с полной строкой, включая и контрольный столбец, всегда следует выполнять проверку сумм коэффициентов уравнений правой и левой частей с полученным новым значением контрольного столбца. Они должны совпадать в пределах округлений результатов. Если этого не делать, то погрешность в вычислениях выявится только после решения систем уравнений. А процесс этот довольно трудоемкий, и без постоянного контроля вся работа может оказаться напрасной.

Из математики известно, что результат решения не изменится, если:

— любую строку матрицы поменять местами с другой строкой;

— любую строку матрицы умножить или разделить на одно и то же постоянное число.

Решение матрицы сводится к образованию т.н. треугольной матрицы вида

.(14.55)

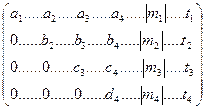
Таким образом получается система линейных уравнений

для, например, четырех линейных уравнений. Из последней строки находят значение k₄ :

(14.57)

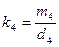
и последовательной подстановкой в уравнения (14.56) решают задачу.

Контроль решения осуществляется подстановкой полученных значений k в исходные уравнения (14.53).

Проследим решение на приведенном примере.

Шаг 1. Образовать 1-й нулевой столбец в строках 2, 3 и 4 матрицы (14.54). Для этого умножим 2-ю и 4-ю строки на (+2), а 3-ю строку – на (-4/3). Получим:

.(14.58)

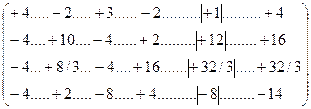
Затем последовательно сложим 2-ю, 3-ю и 4-ю строки (14.58) с первой строкой этой матрицы:

.(14.59)

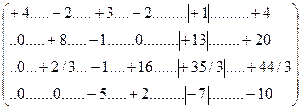
Шаг 2. Образовать 2-й нулевой столбец в строках 3 и 4 (14.59). При этом в примере для строки 4 нет необходимости в преобразованиях, поскольку в ней на второй позиции уже имеется ноль. В связи с этим достаточно преобразовать только 3-ю строку. Для этого умножим ее на (-12)

(14.60)

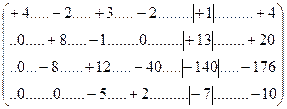
и сложим полученную строку со 2-й строкой той же матрицы:

.(14.61)

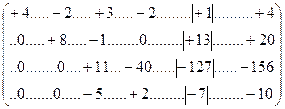
Шаг 3. Образовать нулевой 3-й столбец (14.61) в строке 4, для чего требуется умножить его на (+2,2)

(14.62)

и сложить со строкой 3 этой же матрицы (14.62):

(14.63)

В результате система линейных уравнений (14.53) преобразуется к виду:

Из уравнения 4 (14.64) находим k₄ = +4. Из уравнения 3 подстановкой в него значения k₄ находим k₃ = +3. Из уравнения 2 подстановкой k₃ (коэффициент при k₄ равен нулю) находим k₂ = +2. Из уравнения 1, после подстановки значений k₂ , k₃ и k₄ , находим k₁ = +1.

В качестве замечаний к решению систем линейных уравнений необходимо указать следующее. При уравнивании значения коэффициентов и свободных членов системы линейных уравнений часто являются не целыми числами, а дробными. В связи с этим рекомендуется величины весов и обратных весов округлять до 0,01 – 0,001 ед., значения коэффициентов при неизвестных округлять до 0,0001ед., получаемые значения неизвестных округлять до 0,001 – 0,0001 ед. При этом, как указывалось выше, поправки в углы часто округляют до 0,1″ – 0,01″ , в расстояния (приращения координат) – до 1 мм, в превышения – до 0,1 – 1,0 мм.

135.2. Решение систем линейных уравнений по алгоритму Гаусса

В основе алгоритма Гаусса лежит метод последовательного исключения неизвестных, рассмотренный выше. Алгоритм весьма прост вследствие простых однотипных действий на каждом последующем шаге вычислений. При этом обеспечивается надежный контроль промежуточных результатов. Кроме того, алгоритм Гаусса упрощает решение систем линейных уравнений при введении в них дополнительных граф, необходимых для вычисления весов уравненных элементов или их функций (об этом будет сказано позже).

Алгоритм Гаусса рассмотрим на примере системы четырех линейных уравнений вида:

;

; (14.65)

;

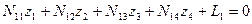
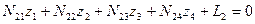
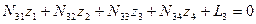
Укажем, что в этой системе линейных уравнений, составленных при решении задачи уравнивания, коэффициенты с одинаковыми двойными индексами являются квадратичными (диагональными). Диагональные коэффициенты по условию их получения при составлении условных линейных уравнений всегда положительные. Коэффициенты, имеющие обратные индексы, равны между собой. В связи с симметрией коэффициентов относительно диагональных таблицу коэффициентов обычно записывают сокращенно в таком виде:

, (14.66)

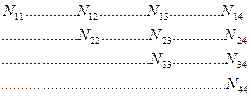
имея в виду наличие и симметричных коэффициентов на незаполненных местах.

Составим т.н. элинимационное уравнение, которое в алгоритме Гаусса обозначают буквой Е. Это уравнение представляет собой выражение первого неизвестного z₁ через остальные (уравнение Е₁):

. (14.67)

Подставим в уравнения (14.65) полученное значение z₁ и запишем новую систему линейных уравнений без неизвестного z₁:

;

; (14.68)

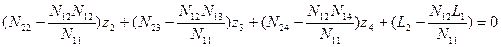
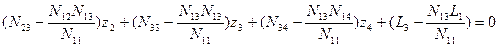
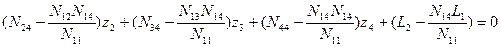
Введем следующие обозначения:

; ; ;

; ; .

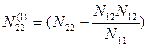
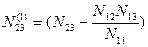
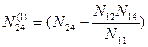
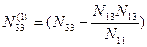
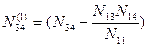
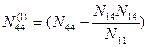
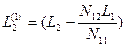
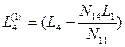
Для полученных коэффициентов сохраняются все особенности системы линейных уравнений с диагональными коэффициентами, имеющими одинаковые двойные индексы (22, 33, 44 и т.д., если уравнений более 4-х). Таким образом, можно записать преобразованную систему линейных уравнений:

;

; (14.69)

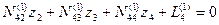
Составим второе элинимационное уравнение Е₂ :

. (14.70)

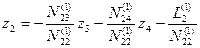
Подставим значение z₂ в уравнения (14.69):

;

. (14.71)

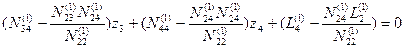
Снова введем обозначения:

; ; ;

; .

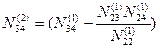
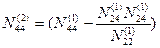
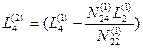
В результате получим систему линейных уравнений с двумя неизвестными:

(14.72)

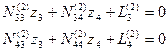
Третье элинимационное уравнение (Е₃) в этом случае имеет вид:

(14.73)

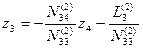
Подставим значение z₃ в уравнения (14.72), получим

. (14.74)

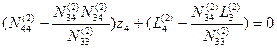
Введя в уравнение (14.74) соответствующие обозначения, как и в предыдущих случаях, получим окончательное уравнение с одним неизвестным в обозначениях Гаусса:

. (14.75)

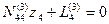
Из уравнения (14.75) найдем

. (14.76)

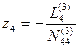
Затем, для определения остальных неизвестных, воспользуемся последовательно элинимационными уравнениями Е₃ , Е₂ и Е₁ , в результате чего получим значения z₃ , z₂ и z₁.

Обратим внимание на то, что для определения неизвестных нужны только элинимационные уравнения. Остальные уравнения не используются.

Представим схему решения системы четырех линейных уравнений в виде таблицы Гаусса (табл. 14.1).

Запись коэффициентов N в строке (3), (7), (12) сокращенная, только вправо от диагональных коэффициентов. Но контрольная сумма этой строки учитывает все коэффициенты, стоящие слева от диагонального. В первой строке записываются все коэффициенты.

После заполнения с вычислениями и контролем строк (1), (2), (3) и (4), что не требует пояснений, заполняют строку (5). Коэффициенты в этой строке равны сумме (3) и (4) строк по столбцам. По аналогии со строкой (2) получают коэффициенты второго элинимационного уравнения Е₂. В строку (7) заносят в сокращенном виде коэффициенты и свободный(ые) члены третьего нормального уравнения. После вычисления строк (8) и (9) по суммам в столбцах строк (7), (8) и (9) получают коэффициенты строки (10). Все дальнейшие действия аналогичны приведенным выше до вычисления коэффициентов в данном случае последнего элинимационного уравнения Е₄. Коэффициент N₅₅ представляет собой указанную в строке (18) сумму произведений весов на квадраты свободных членов. При суммировании столбца по значениям строк (18) – (22) получают значение N₅₅ (4) = [pv 2 ].

Значения неизвестных z_i получают с помощью элинимационных уравнений:

;

; (14.77)

;

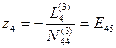
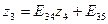
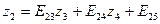
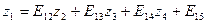
Рассмотрим пример решения системы линейных уравнений по алгоритму Гаусса. Для этого решим систему уравнений (14.53)

Решение уравнений выполним по приведенному выше алгоритму в табл. 14.2.

В табл. 14.2 приведен только пример вычисления неизвестных х без оценки точности (указанные примеры будут рассмотрены отдельно).

Алгоритм Гаусса решения систем линейных уравнений

№№ п/п	Дейст-вия	z₁	z₂	z₃	z₄	L	∑
N₁	N₁₁	N₁₂	N₁₃	N₁₄	L₁	∑₁
Е₁	— 1		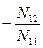			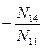∑_E1
N₂	N₂₂	N₂₃	N₂₄	L₂	∑₂
E₁₂N	E₁₂N₁₂	E₁₂N₁₃	E₁₂N₁₄	E₁₂L₁	E₁₂∑₁
N₂ (1)	N₂₂ (1)	N₂₃ (1)	N₂₄ (1)	L₂ (1)	∑_N2 (1)
E₂	— 1		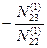		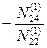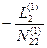∑_E2
N₃	N₃₃	N₃₄	L₃	∑₃
E₁₃N	E₁₃N₁₃	E₁₃N₁₄	E₁₃L₁	E₁₃∑₁
E₂₃N (1)	E₂₃N₂₃ (1)	E₂₃N₂₄ (1)	E₂₃L₂ (1)	E₂₃∑_N2 (1)
N₃ (2)	N₃₃ (2)	N₃₄ (2)	L₃ (2)	∑_N3 (2)
E₃	— 1			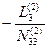∑_E3
N₄	N₄₄	L₄	∑₄
E₁₄N	E₁₄N₁₄	E₁₄L₁	E₁₄∑₁
E₂₄N (1)	E₂₄N₂₄ (1)	E₂₄L₂ (1)	E₂₄∑_N2 (1)
E₃₄N (2)	E₃₄N₃₄ (2)	E₃₄L₃ (2)	E₃₄∑_N3 (2)
N₄ (3)	N₄₄ (3)	L₄ (3)	∑_N4 (3)
E₄	— 1		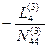∑_E4
N₅	[pll]	∑₅
E₁₅N	E₁₅L₁	E₁₅∑₁
E₂₅N (1)	E₂₅L₂ (1)	E₂₅∑_N2 (1)
E₃₅N (2)	E₃₅L₃ (2)	E₃₅∑_N3 (2)
E₄₅N (3)	E₄₅L₄ (3)	E₄₅∑_N4 (3)
N₅ (4)	N₅₅ (4)	≈ [pv 2 ]