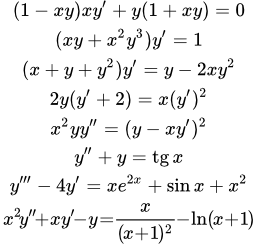Примеры на линейное дифференциальное уравнение

Примеры дифференциальных уравнений с решениями

• Попробуйте решить приведенные ниже дифференциальные уравнения.
• Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021

Линейные дифференциальные уравнения в высшей математике

Содержание:

Линейные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка

В предыдущей лекции мы изучали дифференциальные уравнения с разделяющимися переменными. Другим часто встречающимся типом являются линейные дифференциальные уравнения.

Определение 1. Дифференциальное уравнение вида

(1)

называется линейным дифференциальным уравнением первого порядка. Если , то линейное дифференциальное уравнение (ЛДФУ) (1) можно представить в виде:

, (2)

где .

(3)

называется линейным однородным уравнением, соответствующим уравнению (2).

Уравнение (2) — это уравнение с разделяющимися переменными. Действительно

.

Интегрируя это уравнение, получим

где — произвольная первообразная для функции , а положительная постоянная. Из последнего уравнения находим общее решение уравнение (3):

,

где — постоянная произвольного знака.

Одним из наиболее удобных методов решения уравнения (2) является метод подстановки .

Применим этот метод к уравнению (2). Получим

Приравняем выражение в квадратных скобках к нулю и найдем одно из решений этого дифференциального уравнения. Тогда линейное дифференциальное уравнение (2) будет сведено к системе двух дифференциальных уравнений с разделяющимися переменными

Найдя из системы (4) функции и , запишем общее решение уравнения (2) как .

Пример №122

.

Решение:

Данное уравнение — это ЛДФУ первого порядка (2). Применим метод подстановки .

Составим систему (4):

Решим первое уравнение системы:

Так как нам нужно одно ЧР ДФУ, то возьмем = 1. Имеем

Решаем второе уравнение:

Итак, OP Л ДФУ будет таким:

.

Убедимся проверкой в правильности решения:

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Рассмотрим линейное дифференциальное уравнение (ЛДФУ) второго порядка с постоянными коэффициентами

(5)

где — некоторые константы.

Уравнению (5) соответствует однородное ЛДФУ:

. (6)

Пусть — ОР неоднородного уравнения (5), — ЧР неоднородного уравнения (5), — ОР однородного уравнения (6). Имеет место следующее утверждение.

Теорема 1. Общее решение неоднородного уравнения (5) есть сумма общего решения соответствующего ему однородного уравнения (6) и частного решения неоднородного уравнения (5):

(7)

Рассмотрим однородное ЛДФУ (6). Имеет место следующий результат.

Теорема 2. Пусть — решения уравнения (6), тогда их линейная комбинация , где — произвольные константы, также является решением уравнения (6).

Ранее мы отмечали, что ОР ДФУ 2-го порядка зависит от двух произвольных констант. Из теоремы 2 следует, что функция

(8)

является решением уравнения (6). Возникает вопрос: может ли формула (8) определять ОР ДФУ (6). Если да, то при каких условиях? Чтобы разобраться в этом, введем несколько понятий, аналогичных сведениям из линейной алгебры.

Определение 2. Функции называются линейно независимыми, если их линейная комбинация обращается в ноль, т.е.

,

только лишь в случае . В противном случае они называются линейно зависимыми.

Определение 3. Систему функций , состоящую из двух линейно независимых решений уравнения (6), будем называть фундаментальным набором решений этого уравнения.

Имеет место следующий факт.

Теорема 3. Пусть — фундаментальный набор решений уравнения (6), тогда ОР этого уравнения задается формулой:

(9)

Фундаментальный набор решений уравнения (6) находят методом Эйлера в виде функций . Получаем . Подставляя выражения для , и в уравнение (6), имеем

.

Так как , то это соотношение эквивалентно уравнению

. (10)

Определение 4. Алгебраическое уравнение (10) называется характеристическим уравнением однородного ЛДФУ (6).

При решении характеристического уравнения могут возникать три случая.

Случай 1. Дискриминант характеристического уравнения (10) больше нуля. Тогда существует два действительных и различных решения и кратности 1. Соответствующие им решения , образуют фундаментальный набор и ОР уравнения (6) имеет вид

.

Пример №123

.

Решение:

Корнями характеристического уравнения

являются числа = 1 и =-2. Следовательно, ОР однородного ЛДФУ имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 2. Дискриминант = 0. У характеристического уравнения существует единственный действительный корень кратности 2. Ему соответствует решение . Вторым решением из фундаментального набора будет функция .

Таким образом, ОР имеет вид

.

Пример №124

.

Решение:

имеет единственный действительный корень = -3 кратности 2. Поэтому ОР имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 3. Дискриминант

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Линейные дифференциальные уравнения первого порядка

Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.

Общий вид линейного дифференциального уравнения первого порядка таков:

,

где и — непрерывные функции от x.

Как решить линейное дифференциальное уравнение первого порядка?

Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций

и линейное дифференциальное уравнения первого порядка примет вид

. (*)

Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:

,

то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися переменными, отличное от нуля. Разделяя в уравнении переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v — решение уравнения, то её подстановка в уравнение даёт

.

Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.

Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.

Пример 1. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!

Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 2. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

.

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

В следующем примере — обещанная экспонента.

Пример 3. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находимu:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.

Пример 4. Решить линейное дифференциальное уравнение первого порядка

.

Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.

В интеграле , .

Тогда .

Интегрируем и находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.

Пример 5. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

В последних двух примерах требуется найти частное решение уравнения.

Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка

при условии .

Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка

при условии .

Перенесём функцию «игрека» в левую часть и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

.

Первый интеграл равен , второй находим интегрированием по частям.

В нём , .

Тогда , .

Находим второй интеграл:

.

В результате получаем функцию u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.