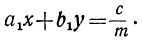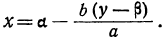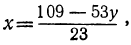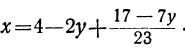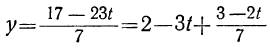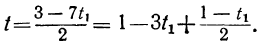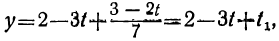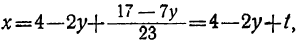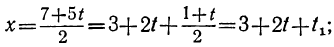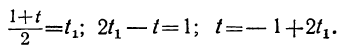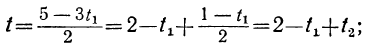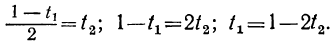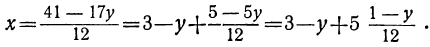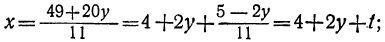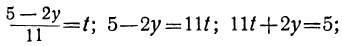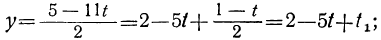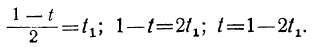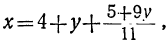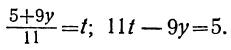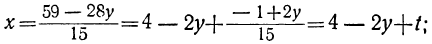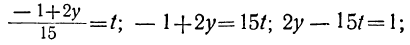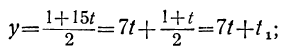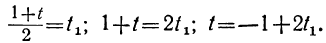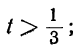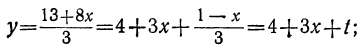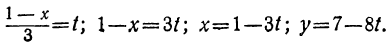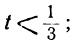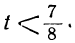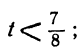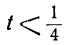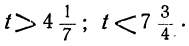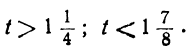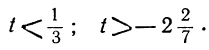Уравнения с двумя переменными (неопределенные уравнения)
Разделы: Математика
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
- повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y 

Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:




Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y 
Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
3) Составим уравнение:
Пусть мальчиков x, x 

Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
- Если y = 3m, m
Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
- Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
- Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.
Ответ: 

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 — 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n
Ответ: 

II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
а) 
б) 
в) 
г) 
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
а)
 |  |  |
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
 |  |  |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
б)
в)
Итоги. Что значит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 — 2n, n  Z Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n  Z Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n  Z Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m  Z Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n  Z Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n  Z Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p  Z Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t  Z Z |
2) Найти целые неотрицательные решения уравнения:
| а) 8x + 65y = 81 | x = 2, y = 1 |
| б) 17x + 23y = 183 | x = 4, y = 5 |
3) Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям
| а) x + y = xy | (0;0), (2;2) |
б)  | (1;2), (5;2), (-1;-1), (-5;-2) |
Число 3 можно разложить на множители:
a)  | б)  | в)  | г)  |
в)  | (11;12), (-11;-12), (-11;12), (11;-12) |
г)  | (24;23), (24;-23), (-24;-23), (-24;23) |
д)  | (48;0), (24;1), (24;-1) |
е)  | x = 3m; y = 2m, m Z Z |
| ж) y = 2x – 1 | x = m: y = 2m – 1, m  Z Z |
з)  | x = 2m; y = m; x = 2m; y = -m, m  Z Z |
и) | решений нет |
4) Решить уравнения в целых числах
 | (-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4) |
| (x — 3)(xy + 5) = 5 | (-2;3), (2;-5), (4;0) |
| (y + 1)(xy – 1)=3 | (0;-4), (1;-2), (1;2) |
 | (-4;-1), (-2;1), (2;-1), (4;1) |
 | (-11;-12), (-11;12), (11;-12), (11;12) |
 | (-24;23), (-24;23), (24;-23), (24;23) |
5) Решить уравнения в целых числах.
а)  | (-1;0) |
б) | (5;0) |
в)  | (2;-1) |
г)  | (2; -1) |
Неопределенные уравнения в математике с примерами решения и образцами выполнения
При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.
Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.
Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.
Задача:
Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.
Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.
Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).
Задача:
Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?
Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.
Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.
Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.
Признак невозможности решения уравнения в целых числах
Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.
Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.
Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.
Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.
Разделив все его члены на m, получим:
При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.
Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.
Признак невозможности решения уравнения в положительных числах
Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.
Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.
Общая формула корней неопределённого уравнения
Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.
Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.
Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или
Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
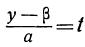
Подставляя в формулу для х число t вместо дроби 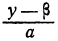
x = a-bt.
Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.
Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.
Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:
- Первым членом формулы является найденное частное значение данного неизвестного.
- Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
- Один из коэффициентов берётся с обратным знаком.
Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.
Пример:
Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.
Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:
| t | 0 | 1 | 2 | 3 | -1 | -2 | … |
| x | 2 | 7 | 12 | 17 | -3 | -8 | … |
| y | 4 | 1 | -2 | -5 | 7 | 10 | … |
Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.
Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.
Способ подстановки
Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.
Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения
Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.
Очевидно, что любому целому значению у будет соответствовать целое же значение х.
Пример:
Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:
| x | 0 | 1 | 2 | 3 | 4 | -1 | -2 | … |
| y | 18 | 13 | 8 | 3 | -2 | 23 | 28 | … |
Общее решение неопределённого уравнения
Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.
Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:
или, исключив целую часть:
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение 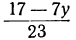
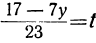
Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 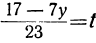
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.
По отношению к новому уравнению поступаем таким же образом. Определяем из него у:
Для того чтобы у было целым, необходимо и достаточно, чтобы 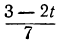
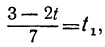
При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:
Приравняв выражение 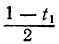
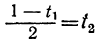
Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.
Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: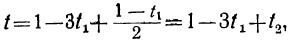
получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:
получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:
получим соответствующие целые значения для х.
Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .
Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.
Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .
Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.
Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:
| t₂ | 0 | 1 | 2 | -1 | -2 |
| x | -16 | 37 | 90 | -69 | -122 |
| y | 9 | -14 | -37 | 32 | 55 |
Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:
- Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.
- Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.
- Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.
Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.
Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:
Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.
Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.
1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.
Пример:
Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.
Решаем последнее уравнение:
Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .
Пример:
Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.
Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.
Решаем последнее уравнение:
Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .
2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.
Пример:
Дано уравнение: 12x+17y=41.
Решаем его относительно х:
Для того чтобы выражение 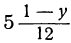
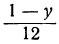
Приравнивая это выражение целому числу t, получим: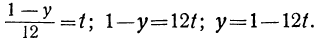
Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t
3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.
Пример:
Дано уравнение: 11х—20y=49.
Решим его относительно х:
Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.
Если бы решали данное уравнение обычным способом, то получили бы для х:
и следующее уравнение было бы:
Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.
Пример:
Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:
Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.
Положительные решения
Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.
Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.
Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.
1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
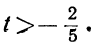
bt > — a ; at 0; 2+-5t>0,
или
Взяв для t любое целое число, большее 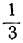
Пример:
Решаем уравнение:
Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или
Любое целое значение t, меньшее 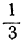
2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:
Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.
Пример:
4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или
Неравенства противоречат друг другу; уравнение не имеет положительных решений.
3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:
Все целые значения t, заключающиеся между 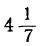
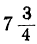
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:
Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.
Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:
Неравенства не противоречат друг другу, но между 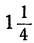
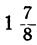
находится ни одного целого числа. Уравнение не имеет целых положительных решений.
Пример:
3x+7y=55.
Решаем уравнение: 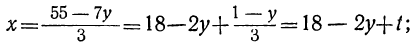
у=1 — 3t; x= 16+7t.
Отсюда:
1 —3t>0; 16+7t> 0,
или
Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:
| t | 0 | -1 | -2 |
| x | 16 | 9 | 2 |
| y | 1 | 4 | 7 |
Пример:
5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
Отсюда:
Неравенства не противоречат друг другу; но между 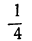
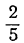
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Неопределенные уравнения
материал (9, 10, 11 класс)
В работе рассматриваются неопределенные уравнения ,методы решения.
Скачать:
| Вложение | Размер |
|---|---|
| neopredelennye_uravneniya.doc | 669.5 КБ |
Предварительный просмотр:
Глава I Диофант и диофантовы уравнения
1.1 «Арифметика» Диофанта 6
1.2 Диофант и способы его решений неопределенных уравнений 14
1.3 Теория чисел по Диофанту 18
1.4 Неопределенные уравнения первой степени 23
1.5 Неопределенные уравнения второго порядка 34
1.6 Неопределенные уравнения третьей степени 41
Глава II Методы решений диофантовых уравнений
2.1 Решение диофантовых уравнений методом «перебора» 45
2.2 Решение диофантовых уравнений методом «спуска» 47
2.3 Решение диофантовых уравнений методом «рассеивания» 51
2.4 Алгоритм Евклида 57
2.5 Цепные дроби 61
2.6 Связь диофантовых уравнений с теоремой Пифагора 66
2.7 Великая теорема Ферма 68
Необычайный рассвет древнегреческой науки IV-III вв. до н.э. сменился к началу новой эры постепенным спадом в связи с завоеванием Греции Римом, а потом и начавшимся разложением Римской империи. Но на фоне этого угасания еще вспыхивает яркий факел. В III веке уже новой эры появляется сочинение александрийского математика Диофанта «Арифметика».
Диофант был одним из самых своеобразных математиков, труды которого имели большое значение для алгебры и теории чисел. До сих пор не выяснены ни год рождения, ни дата смерти Диофанта; полагают, что он жил в III веке н.э.
В одном из древних рукописных сборников задач в стихах¹ жизнь Диофанта описывается в виде следующей алгебраической загадки, представляющей надгробную надпись на его могиле. [6; 374]
«Прах Диофанта гробница покоит: дивись ей – и камень
Мудрым искусством его скажет усопшего век.
Волей богов часть жизни он прожил ребенком
И половину шестой он встретил с пушком на щеках. Только минута седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец. Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей».
Задача-загадка сводится к составлению и решению уравнения:
Речь идет о греческой «Палатинской антологии», изданной в VI в. грамматиком Метродором.
Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Считают, что великий математик жил около 250 года.
Диофант написал большой труд под общим названием «Арифметика», из 13 книг которой только 6 сохранились до наших дней. Эти книги были открыты в Венеции в 1463 г Регимонтаном, который в связи с этим писал, что в произведении Диофанта сосредоточен «весь цвет арифметики, искусство неизвестной»
В сохранившихся книгах Диофанта содержатся 189 задач с решениями. В первой книге изложены задачи, приводящие к определенным уравнениям первой и второй степени. Остальные же 5 книг содержат в основном неопределенные уравнения. В этих книгах еще нет систематической теории неопределенных уравнений, методы решения меняются от случая к случаю. Диофант довольствуется каким-нибудь одним решением, целым или дробным, лишь бы оно было положительным. Тем не менее, решения составляют основной вклад Диофанта в математику.
В работе рассматривается вопрос о видах диофантовых уравнений и способах их решений.
Основная цель — изучить диофантовы уравнения и методы их решения.
Цель исследования определяет следующие задачи:
1)Изучить исторический аспект.
2)Выделить виды диофантовых уравнений.
3)Рассмотреть методы решения неопределенных уравнений.
4)Выявить специфические особенности решения задач с помощью диофантовых уравнений.
5)Выявить связь неопределенных уравнений с теоремой Пифагора.
К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами. Решение уравнений в целых числах — очень увлекательная задача. Задачи диофантовой «Арифметики» решаются с помощью уравнений, а проблемы решения уравнений относятся скорее к алгебре, чем к арифметике.
Решение задач с помощью диофантовых уравнений имеют специфические особенности. Во-первых, они сводятся к уравнениям или системам уравнений с целыми коэффициентами. Как правило, эти системы неопределенные, то есть число уравнений в них меньше числа неизвестных.
Во-вторых, решения требуется найти только целые, часто натуральные. Для выделения таких решений из всего бесконечного их множества приходится пользоваться свойствами целых чисел, а это уже относится к области арифметики.
Тема актуальна и значима в школьном курсе, так как расширяет представления об уравнениях с несколькими переменными, развивает познавательную активность, интерес к математике.
Поскольку тема интересна, требует сообразительности, напряженной работы ума, исследовательского подхода к рассматриваемой проблеме, поэтому очень часто задачи встречаются в материалах математических олимпиад различных уровней.
Сообщение исторических сведений по математике является одной из форм воспитания научного мировоззрения, способствуют лучшему усвоению науки, воспитывает отношение к математике как части общечеловеческой культуры. Без математики человека нельзя назвать культурным. Как отмечают современные ученые, требования нашего времени таковы, что каждому специалисту, будь то естествоиспытатель или гуманитарий, необходимы знания в области математики. Математика – язык, который связывает науки между собой. Математика есть продукт творческой деятельности человеческого гения в течение тысяч лет, а не хитрая выдумка какого-то одного «мудреца». Каждая теорема, каждое уравнение – это обобщение гигантского опыта человечества, подведение итогов многовековой работы человеческой мысли.
ГЛАВА I ДИОФАНТ И ДИОФАНТОВЫ УРАВНЕНИЯ
1.1 «Арифметика» Диофанта
Диофант открыл новую главу в математике, и невозможно выявить, какие невидимые источники питали его творчество.
С 16 века известны только 6 книг из его великого труда « Арифметики». Они содержатся в греческом манускрипте, обнаруженные в 1464 году Регимонтаном в Венеции и явившемся копией более древнего манускрипта. Неясно, где располагались семь недостающих книг в общей структуре трактата. Тот кажущийся беспорядок, в котором находится этот труд, и который мог возникнуть в результате переписок и вмешательства позднейших комментаторов, дал пищу для множества противоречивых интерпретаций в ХIХ веке.
Ныне возникла опасность, что прежнее прочтение Диофанта окажется неверным, и анализ его труда нужно будет проводить заново. Действительно, недавно в Иране (1972 г.) были обнаружены и идентифицированы четыре из арифметических книг Диофанта [4; с.104]. Речь идет об арабском манускрипте, датируемом 1175г., который оказался копией знаменитого перевода Диофанта на арабский язык, приписываемого Коста ибн Лука (умер около 912 г.), под названием «Искусство алгебры».
Арабские книги помечены номерами 4, 5, 6 и 7, и первое исследование Рашеда, по-видимому, указывает на то, что они идут за греческой книгой III. Вообще проблему числа и порядка книг «Арифметики» историки математики должны полностью пересмотреть. Может оказаться, что труд Диофанта еще более значителен, чем казалось раньше.
«Арифметику» нельзя считать теоретическим трудом по арифметике в пифагорейском смысле – пифагорейцы термин «арифметика» предназначали для теории чисел, которая считалась дисциплиной без определенного метода, но требующей от ума некоего рода божественной интуиции. А этот трактат ближе всего к традициям вычислительной математики, или логистики. Однако в период, когда Диофант работал над составлением своей книги, это первоначальное различие уже, по-видимому, стерлось – это видно и из самого выбора названия и из того, что практические задачи у Диофанта всегда сначала формулируются в абстрактной форме, а числовые данные вводятся позже. Эта общая и абстрактная формулировка радикальным образом отличает Диофанта от Вавилонских математиков.
Разумно считать «Арифметику» компиляцией, аналогичной «Началам» Евклида, составленной одним автором, но являющейся плодом коллективной традиции.
Диофант выделяет среди чисел квадраты, кубы, биквадраты, квадратокубы, наконец, кубокубы. Наименование степеней основано на сложении показателей степеней, то есть квадратокуб — это квадрат, умноженный на куб. Диофант указывал, что решение большого числа арифметических задач приводит к операциям над числами различного вида, то есть к оперированию с различными степенями неизвестного. Он ввел символы для шести первых положительных и шести первых отрицательных степеней неизвестных.
Неизвестное Х определяется как неопределенное кратное единицы, однако на деле это означает, что его значение может быть рациональным; оно просто называется числом. Числа, не являющиеся коэффициентами при неизвестных, называются единицами и обозначаются символом М. Появился знак вычитания, в то время как сложение чисел обозначается просто написанием их друг за другом.
Наконец, Диофант вставлял слова «часть от» между двумя алгебраическими выражениями в том месте, где мы ставим черту дроби.
Число неизвестных могло достигать шести, но Диофант имел обозначение только для одного. Когда их было несколько, он говорил о первом, о втором, самом большом, самом маленьком и т.д. неизвестном или выражал неизвестные через одно из них. В этом отношении его текст бывает иногда весьма темным.
Диофант написал свой труд в классической форме непрерывного рассуждения. Но он сократил немного этот словесный поток, систематически используя некоторые сокращения для степеней чисел, а также для операций, и заменил некоторые часто встречающиеся слова их начальными и конечными буквами. Но алгебраических манипуляций над этими сокращениями он никогда не производил. Эта стадия эволюции алгебраической записи, промежуточная между чисто описательной, словесной стадией алгебраического символизма, которая сложилась в ХVII веке, была названа синкопированной. Диофант проводил над своими символами все алгебраические операции, которые мы проводим теперь (возведение в степень, приведение подобных, подстановки и т.д.). Отличие от алгебры ХVI-ХVII вв. состояло в том, что у Диофанта не было обозначений для параметров. Им приходилось придавать всякий раз конкретное числовое значение. Таким образом, в «Арифметике» впервые была введена буквенная символика. Более того, в «Арифметике» мы находим впервые запись уравнений (с числовыми коэффициентами), там же формулируются и первые операции с уравнениями, ставшими впоследствии известными под арабскими названиями «ал-джабр» и «ал-мукабала».
Книга I в греческом варианте посвящена определенным задачам первой и второй степени с одним или несколькими неизвестными. Например: «Найти два таких числа, чтобы их сумма и произведение равнялись заданным числам». Нужно, чтобы квадрат полусуммы искомых отличался от их произведения на квадрат. Это необходимое условие формирования. Пусть их сумма будет 20, а произведение 96» (1,27).Диофант действовал следующим образом: он полагал, что разность двух чисел равна двум аритмам (аритм обозначал неизвестную величину), скажем 2d. Тогда эти два числа равны 10+d и 10-d. Имеем (10 + d) (10 –d ) = 96, то есть 100 — d² = 96 и d = 2. В современных обозначениях, если х и у-искомые числа, полагаем
Получаем ху = 100 — d² = 96, откуда d = 2.
Первое число равно 10 + 2 = 12, второе 10 – 2 = 8.
Таким образом, условие разрешимости выражается соотношением
(( ) 2 – ху) 2 = полный квадрат. (1.1.1)
У Диофанта оно имеет целью получение лишь рациональных положительных решений.
Действительно, если мы положим х + у = а и ху = b, то получим значения , которые будут рациональными, если ( ) 2 – b = полный квадрат, что непосредственно дает (1.1.1)
Данная задача возвращает нас к задаче из «Начал» Евклида, состоящей в отыскании двух чисел, сумма и произведение которых известны. Можно заведомо констатировать отсутствие обращений к какому бы то ни было геометрическому построению и обнаружить начатки разрешающего алгоритма, который бесспорно роднит Диофанта с вавилонянами. Эта разрешающая процедура присутствует во многих аналогичных задачах, состоящих в решении систем уравнений с двумя неизвестными, и приводит с помощью исключения к квадратному уравнению. На самом деле квадратных уравнений как таковых у Диофанта нет, хотя он и обещал во введении их рассмотреть, но, тем не менее, многие примеры доказывают, что он был знаком с их решением. Коэффициенты уравнений были всегда рациональными положительными числами, часто даже целыми, и если уравнение не имело рациональных положительных корней, Диофант его отбрасывал и объявлял не имеющим смысла; иногда он изменял числовые значения, чтобы сделать уравнение разрешимым в его смысле. В противоположность Герону Александрийскому или Архимеду, допускавшим в решении геометрических задач иррациональные числа, которые они затем пытались найти приближенно, Диофант проявил себя большим приверженцем арифметики и алгебры. Для него статус чисел распространялся лишь на положительные рациональные числа. Разумеется, отрицательное решение было немыслимо.
Наконец, если уравнение второй степени имеет два допустимых корня, Диофант либо упоминал лишь об одном из них, либо, если он находил эти два решения с помощью различных процедур, то не пытался объединить их общим представлением.
Пять других книг в основном посвящены неопределенным уравнениям, то есть уравнениям и системам уравнений со многими неизвестными, которые, вообще говоря, имеют большое число решений. И здесь Диофант ограничился исключительно рациональными решениями. Можно сказать, что это наиболее новая тема «Арифметики» Диофанта. (В настоящее время исследования целочисленных решений этого типа неопределенных уравнений называют диофантовым анализом).
Можно сказать, что, изучив сто решений Диофанта, невозможно предвидеть сто первое; и действительно, каждая из 189 задач решалась особым способом благодаря разумному выбору вспомогательного неизвестного и блестящим вычислительным приемам, учитывающим конкретные свойства чисел, выбранных в качестве числовых значений. Самые трудные дроби не пугали Диофанта – вообще он любил вычисления.
В общем случае при решении систем неопределенных уравнений он уменьшал число неизвестных, подставляя вместо них произвольные рациональные значения или выбирая вспомогательные неизвестные. Так, некоторые задачи с неопределенными уравнениями изменяли характер в ходе решения, поскольку он доопределял одну или несколько неизвестных произвольным образом, что сводило их к задачам с определенными уравнениями.
Приведем пример неопределенной задачи Диофанта [4; с.111].
Задача 1. «Найти такие три числа, чтобы квадрат суммы всех трех, вычтенный из каждого числа, давал квадрат. Положим сумму этих трех чисел аритмом.»
Условия задачи можно перевести так:
Диофант полагал X + Y + Z = x, откуда (X + Y + Z)² = x².
Затем он сделал следующие подстановки:
X = 2x², Y = 5x², Z = 10x²,
которые обращали все три уравнения в тождества α² = x², β² = 4x²,γ² = 9x².
Затем он подставлял эти значения в соотношение X + Y + Z = x и получал 2х² + 5х² + 10х² = х или 17х² = х, откуда х = , х² =
Решение Диофанта таково: Х = Y = , Z = .
Он редко приводил полное семейство решений.
Хотя ни один общий результат в «Арифметике» не был сформулирован, Диофант явно ссылался на леммы, возможно доказанные в работе, озаглавленной «Поризмы» и полностью утерянной.
Речь идет о тождествах, которые можно квалифицировать как алгебраические, таких, как
[( )] 2 + mn = [( )] 2 , или (m 2 -n 2 ) 2 + (2mn) 2 = (m 2 +n 2 ) 2 ;
второе является тождеством для пифагоровых троек. Например, в задаче из греческой книги III Диофанту нужно было построить четыре прямоугольных треугольника с одинаковой гипотенузой. Он исходит из двух пифагоровых троек: 3, 4, 5 и 5, 12, 13 и, умножая каждый «треугольник» на «гипотенузу» другого, выводит из них две новые пифагоровы тройки: 39, 52,65 и 25,60,65.
Но, пишет далее Диофант, 65 записывается также в виде 16+49 и 64+1, «а это происходит потому, что 65 получается от произведения 13 и 5, а каждое из этих чисел раскладывается на два квадрата».
В действительности он использовал здесь тождество
a = 2, b = 1, c = 2, d = 3,
5·13 = 65 = 4² + 7² = 8² + 1².
Затем отсюда с помощью пифагоровых троек он выводит при m = 7, n = 4 и m = 8, n = 1, что
Числа, выбранные для этого примера, позволяют предположить, что Диофант знал, что всякое простое число вида 4n + 1 является суммой двух квадратов.
Судя по выбираемым им числовым значениям, Диофант, вероятно, был знаком со многими свойствами чисел, например с тем фактом, что число вида 4n + 3 не является суммой двух квадратов, число вида 8n + 7 не является суммой трех квадратов и т.д., но эти свойства нигде не были им высказаны явно(V; 9,11,14).
Многие из них были сформулированы, а затем доказаны Ферма и его исследователями в ХVIII веке и легли в основу современной теории чисел.
«Арифметика» Диофанта предполагала хорошее знакомство со свойствами целых и рациональных чисел и подразумевала знание определенных приемов алгебраического характера: преобразования выражений, подстановок, исключения и т. д., даже если это явно не оговаривалось.
В греческой математике этот труд представлял собой новое по своей сути слово, как в смысле содержания, так и методов, которые означали разрыв с традиционными геометрическими методами. Однако именно эти последние воспринимались впоследствии как основное греческое наследие, в то время как влияние Диофанта оказалось скрытым.
http://lfirmal.com/neopredelennye-uravneniya/
http://nsportal.ru/shkola/materialy-metodicheskikh-obedinenii/library/2019/10/28/neopredelennye-uravneniya