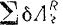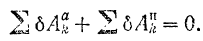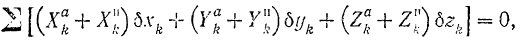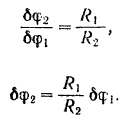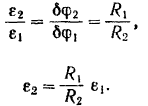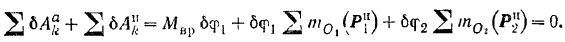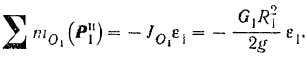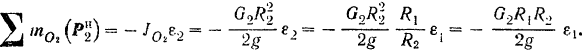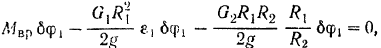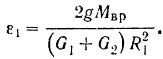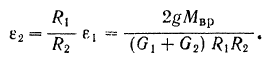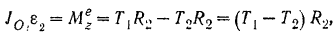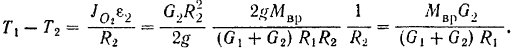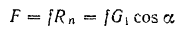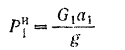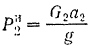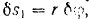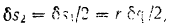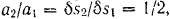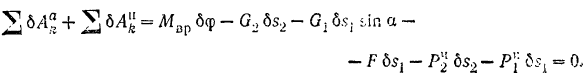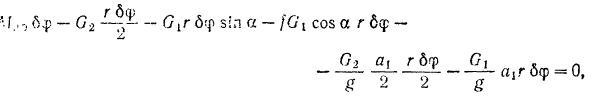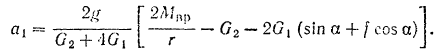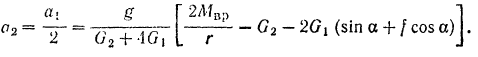Общее уравнение динамики. Пример решения задачи
Условие задачи
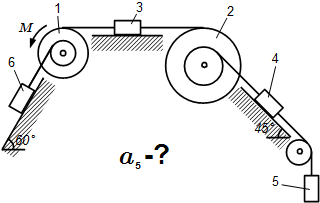
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R 1 = 0,2 м , r 1 = 0,1 м , а шкива 2 – R 2 = 0,3 м , r 2 = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ 1 = 0,1 м и ρ 2 = 0,2 м .
Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.
Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).
Решение задачи
Дано: R 1 = 0,2 м , r 1 = 0,1 м , R 2 = 0,3 м , r 2 = 0,15 м , ρ 1 = 0,1 м , ρ 2 = 0,2 м . P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н , M = 10 Н·м .
Установление кинематических соотношений
Установим кинематические соотношения. Пусть V 4 , V 5 , V 6 , a 4 , a 5 , a 6 , δS 4 , δS 5 , δS 6 – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω 1 , ω 2 , ε 1 , ε 2 , δφ 1 , δφ 2 – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.
Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.
Итак, мы нашли связь между скоростями тел.
;
;
.
Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.
Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.
Активные внешние силы
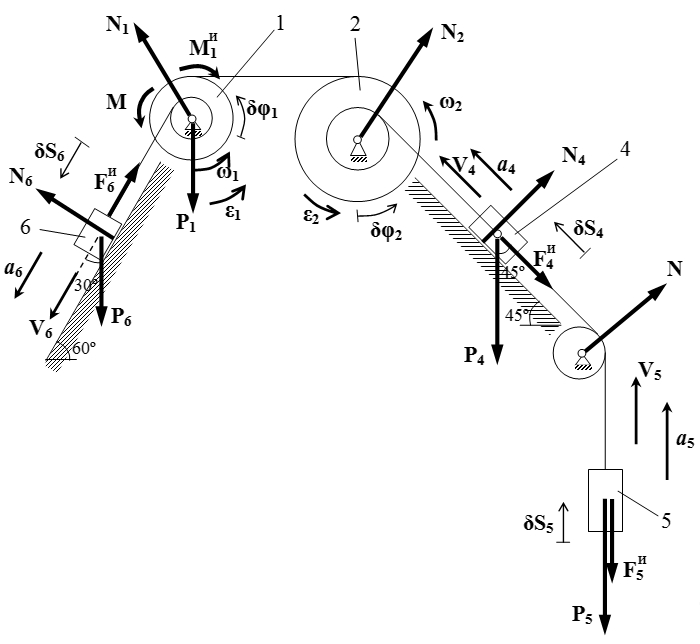
Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P 1 = 40 Н , P 4 = 20 Н , P 5 = 30 Н и P 6 = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N 1 , N 2 и N шкивов 1, 2 и невесомого блока;
силы реакции N 4 и N 6 , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.
Силы инерции
Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.
Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε 1 и ε 2 , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a 4 , a 5 и a 6 , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a 5 . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).
Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a 5 .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.
Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.
Применение общего уравнения динамики
Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS 5 . Тогда угол поворота δφ 1 шкива 1 и перемещения δS 4 и δS 6 грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.
Определение суммы работ внешних активных сил и сил инерции
Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.
Работа, произведенная моментом сил , вычисляется аналогично:
.
Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P 1 , N 1 , N 2 и N не совершают работу. Поскольку силы N 4 и N 6 перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.
Находим сумму работ остальных активных сил и сил инерции.
.
Подставляем выражения для сил инерции и применяем кинематические соотношения.
.
Сокращаем на δS 5 и преобразовываем.
.
Подставляем численные значения.
;
;
м/с 2 .
Автор: Олег Одинцов . Опубликовано: 02-08-2015
iSopromat.ru
Рассмотрим общее уравнение динамики механической системы, которое также называется принципом Даламбера-Лагранжа:
Объединяя этот принцип с принципом возможных перемещений для систем с идеальными связями получаем уравнение:
которое называют общим уравнением динамики (или принципом Даламбера-Лагранжа).
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нолю.
Поскольку в уравнении присутствуют силы инерции, а следовательно и ускорения, то эти уравнения представляют собой дифференциальные уравнения движения механической системы с идеальными связями.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Общее уравнение динамики
Общее уравнение динамики
Используя метод кинетостатики, мы можем условно приложить ко всем точкам движущейся системы силы инерции этих точек. Во всякий момент движения системы совокупность действующих на нее активных сил, реакций связей н условно приложенных сил инерции точек системы будет формально удовлетворять условию равновесия системы, выражаемому принципом возможных перемещении.
Согласно этому принципу при всяком возможном перемещении системы сумма элементарных работ всех приложенных к ней сил равна нулю.
Если наложенные связи на систему идеальные, то, как известно, сумма элементарных работ реакций таких связей при всяком возможном перемещении системы равна нулю. Таким образом, для системы с идеальными связями сумма
элементарных работ реакций связей из выражения для суммы элементарных работ всех приложенных сил выпадает, и мы получаем уравнение, носящее название общего уравнения динамики:
Во всякий момент движения системы с идеальными связями сумма элементарных работ всех прилоохенных к ней активных сил и сил инерции точек системы, условно приложенных к этим точкам, равна нулю на всяком возможном перемещении системы.
Пользуясь аналитическим выражением (189) элементарной работы, уравнению (217) можно придать и другую форму:
где 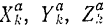
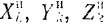
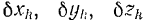
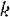
В случае, когда связи неидеальные и трением в них пренебречь нельзя, то, применяя общее уравнение динамики, надо включать силы трения в число активных сна, действующих на систему.
Приняв общее уравнение динамики за исходное, можно вывести из него все общие теоремы динамики. Оно как бы включает в себя всю механику, отчего и возникло его название.
Пример задачи:
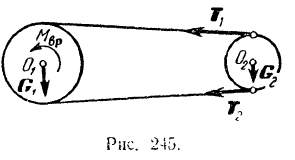
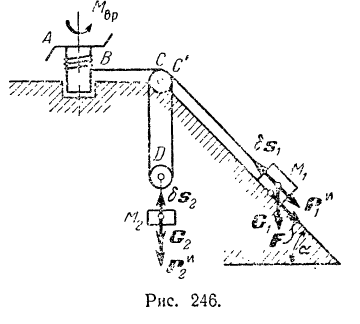
Два шкива, соединенные бесконечным ремнем, вращаются вокруг неподвижных параллельных осей 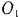
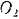
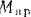
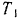
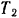
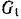
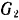
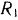
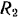
цилиндрами. Трением в осях, скольжением ремня и его пренебречь.
Решение:
Присоединим к активным силам, действующим на систему (шкивы — ремень), силы инерции шкивов и дадим ведущему шкиву возможное перемещение — поворот на бесконечно малый угол 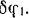
Соответствующее перемещение ведомого шкива находится из соотношения
В аналогичной зависимости находятся и угловые ускорения шкивов:
Составляем общее уравнение (217) динамики:
По формуле (212) сумма моментов сил инерции точек ведущего шкива относительно его оси 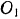
По той же формуле, сумма моментов сил инерции точек ведомого шкива относительно его оси 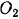
Подставляя соответствующие значения в общее уравнение динамики, будем иметь:
откуда находим угловое ускорение ведущего шкива
Угловое ускорение ведомого шкива
Для того чтобы определить разность 
откуда искомая разность натяжений ремня:
Пример задачи:
Вал кабестана (вертикального ворота) радиуса 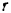
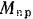
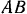
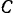
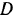
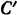
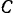
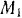
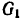
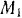
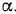
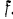
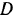
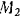
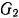
Решение:
Отнесем к активным силам, действующим на данную систему, силу трения 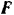
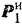
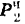
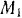
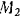
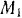
и направлена вдоль наклонной плоскости вниз. Сила инерции груза 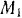
и направлена вдоль наклонной плоскости вниз. Сила инерции груза 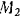
и направлена вертикально вниз.
Дадим валу кабестана возможное перемещение — поворот на элементарный угол 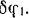
где 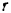
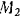
так как подвижный блок висит на двух ветках троса.
Ускорения грузов 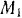
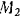
Составляя общее уравнение динамики, будем иметь:
Выражая в последнем равенстве все перемещения через 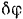
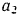
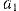
откуда ускорение груза 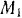
Легко находится теперь и ускорение груза 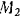
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://isopromat.ru/teormeh/kratkaja-teoria/obschee-uravnenie-dinamiki
http://lfirmal.com/obschee-uravnenie-dinamiki-v-teoreticheskoj-mehanike/