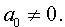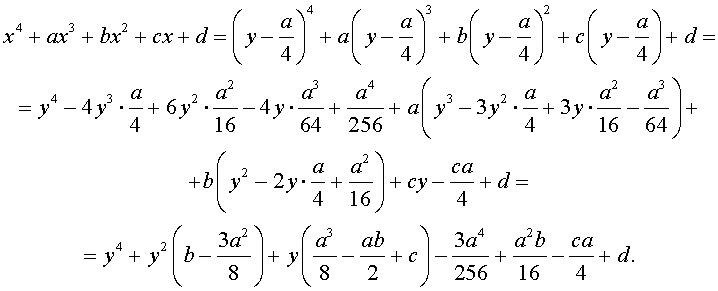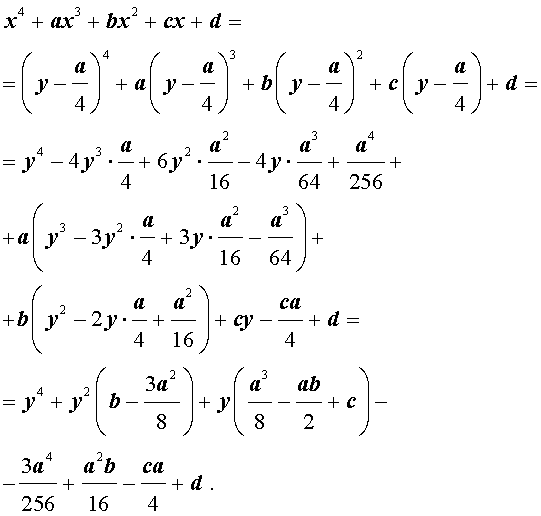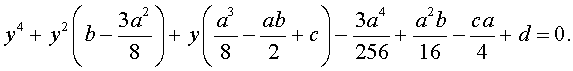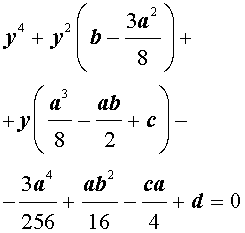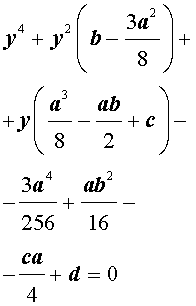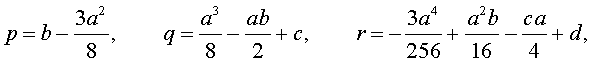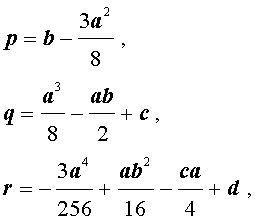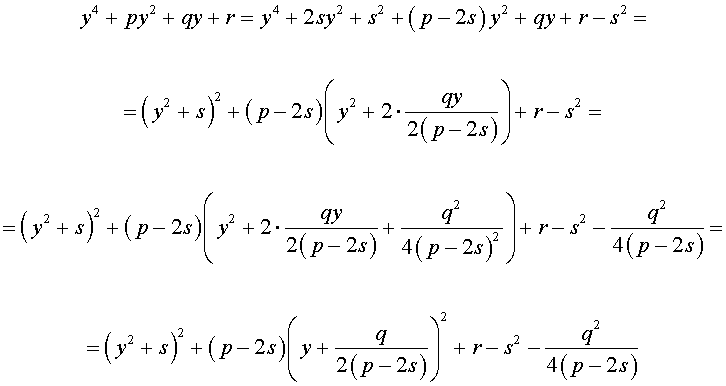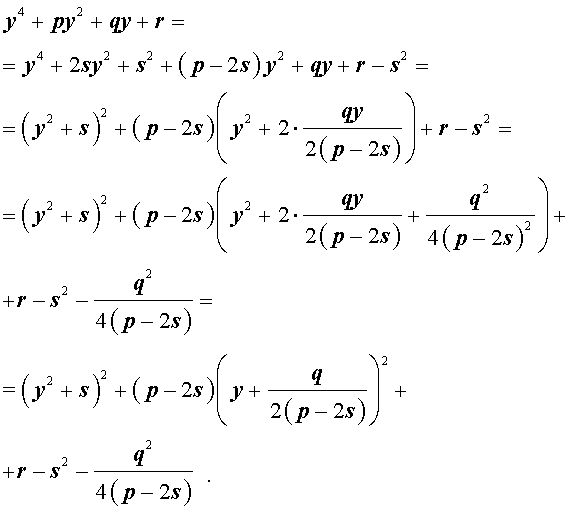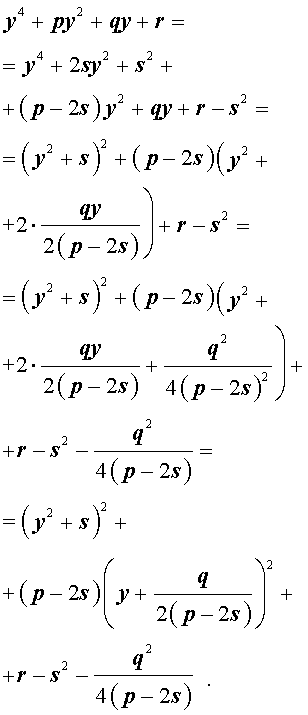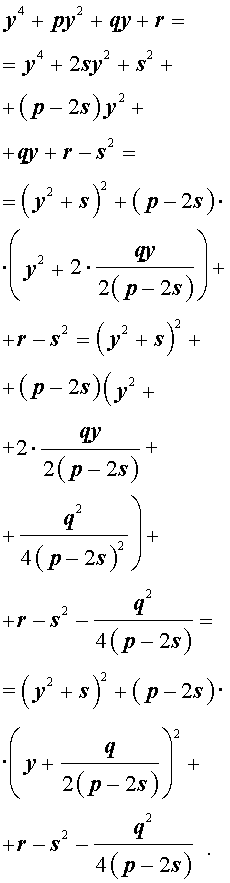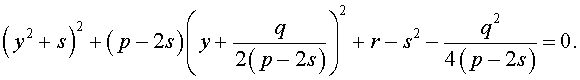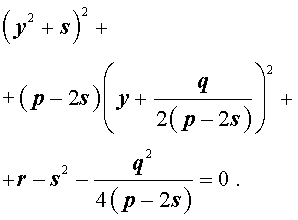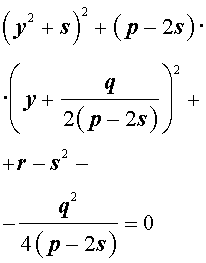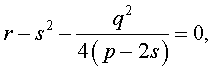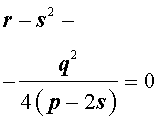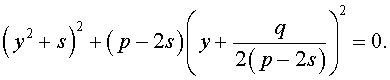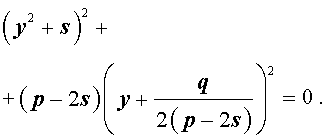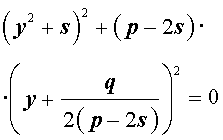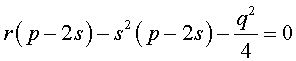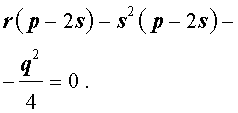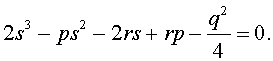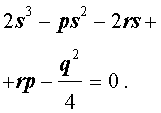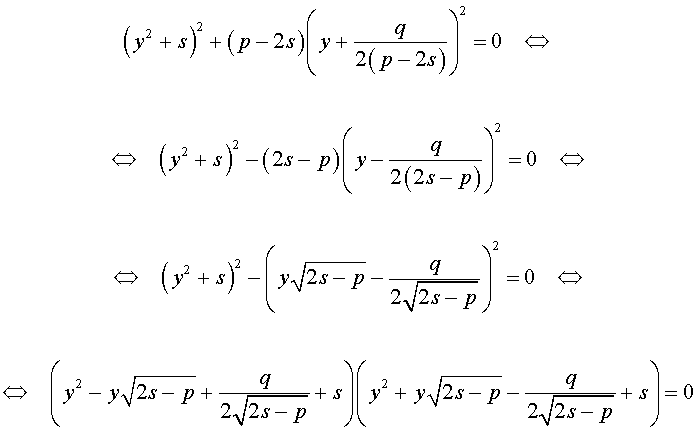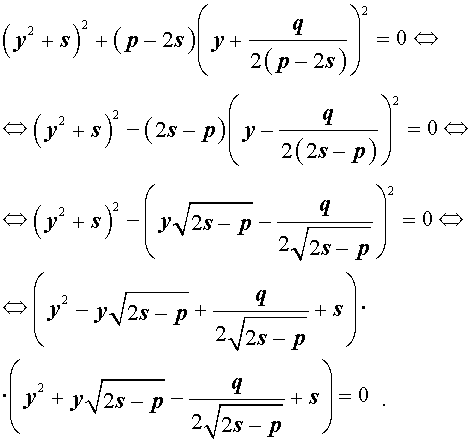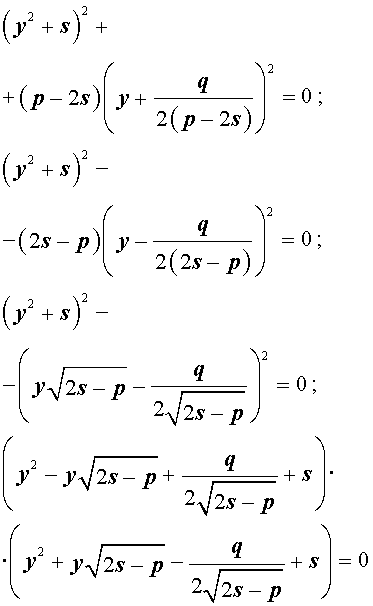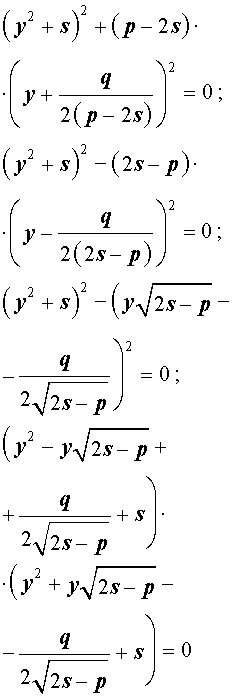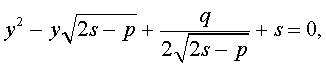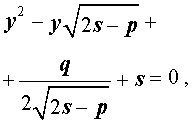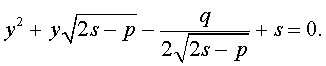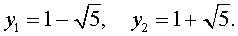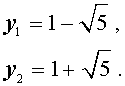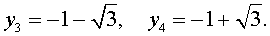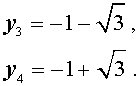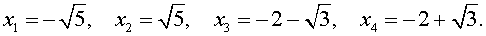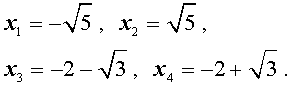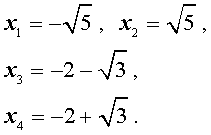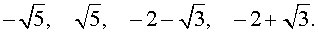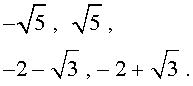Решение уравнений 4-ой степени. Метод Феррари
 Схема метода Феррари Схема метода Феррари |
 Приведение уравнений 4-ой степени Приведение уравнений 4-ой степени |
 Разложение на множители. Кубическая резольвента Разложение на множители. Кубическая резольвента |
 Пример решения уравнения 4-ой степени Пример решения уравнения 4-ой степени |
Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
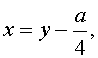 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Переходить к приведенному кубическому уравнению не нужно, так как исходное уравнение само является приведенным, причем р = −6, q = 4 (1 — i).
Таким образом, получаем:

Переходя к приведенному кубическому уравнению, получаем уравнение:
причем х = у + 1 ; р = 9 ; q = −26.
Таким образом, находим:
D = (−13)2 + 33 = 196 , 
u = 
y2 = −1 + 2
y3 = −1 − 2
х1 = 3 ; х2 = 2

Ответ: а) 7 ; 1 + i

в) 3 ; 2

Занятие 16. Решение уравнений четвертой степени методом Феррари
Рассмотрим решение уравнений 4-й степени на конкретном примере.
Пример. Решите уравнение
Оставим в левой части уравнения члены, содержащие х4 и х3 :
Дополним левую часть полученного уравнения до полного квадрата:
х4 − х3 + 


Введем в полный квадрат левой части равенства (1) параметр r :
Откуда с учетом равенства (1) получим:

Подберем значение параметра r таким образом, чтобы дискриминант правой части равенства (2) обратился в нуль (т. е. чтобы в правой части равенства (2) также получился полный квадрат).
D =
= 
Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
В частности, D = 0 , если r = −3/2 .
Подставив значение r = −3/2 в равенство (2) , получим:




х2 − х + 2 = 0 или х2 − 5 = 0 .

Ответ: 
Задача 1. Решите уравнения:
Преобразуем уравнение (1)* по методу Феррари :
Введем в полный квадрат левой части равенства (2)* параметр r . Получим:
Используя равенство (2)*, находим :
Теперь подберем такое значение параметра r , чтобы дискриминант правой части равенства (3)* был равен нулю.

Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
В частности, D = 0 , если r = 2.
Подставив найденное значение параметра r в равенство (3)* получаем:
x2 − 2x + 3 = 0 или x2 + l = 0;

Преобразуем уравнение (4)* по методу Феррари:
Введем в полный квадрат левой части равенства (5)* параметр r . Получим:
Откуда с учетом равенства (5)* находим:
Подберем такое значение параметра r , чтобы дискриминант квадратного трехчлена в правой части равенства (6)* обратился в нуль:
− 2 r 3 + 10 r 2 − 12 r + 4 = 0 ; r 3 − 5 r 2 + 6 r − 2 = 0;
r 3 − r 2 − 4 r 2 + 4 r + 2 r − 2 = 0;
В частности, дискриминант равен нулю, если r = 1. Следовательно, подставив значение r = 1 в равенство (6)* получим:
(х2 − 3 х + 1)2 = х 2 − 4 х + 4 ; (х 2 − 3 х + 1)2 − (х − 2)2 = 0;
х 2 − 2 х − 1 = 0 или х 2 − 4 х + 3 = 0 ;
х 1, 2 = 
Ответ: a)
б) 
ИЗ ИСТОРИИ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ
ПОНЯТИЯ КОМПЛЕКСНОГО ЧИСЛА
В 1494 году в Венеции вышла книга францисканского монаха, занимавшего кафедру математики Миланского университета, Луки Пачиоли (Пачоли) (1450–1510) «Сумма (знаний) по арифметике, геометрии, отношениям и пропорциям» («Summa»), которая заканчивалась выводом: «Решение кубических уравнений вида
где а > 0 и b > 0 , столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой».
Однако, несмотря на это предупреждение, уже через 6 лет в 1500 году профессор Болонского университета Сципион дель Ферро (1456–1526) нашел формулу решения уравнения
где а > 0 и b > 0 . Эта формула имела вид:

Но, как это было принято в ту эпоху, дель Ферро держал свой метод в тайне.
В феврале 1535 года Николо Фонтана из Брешии (1499 (?)–1557), известный под именем Тарталья (что в переводе с итальянского означает «заика» – Фонтана сильно заикался), в ходе публичных состязаний с Фиоре (учеником дель Ферро) решил три десятка кубических уравнений вида:
где m , n , а, b − положительные числа.
В конце 30-х годов XVI века Джероламо (Джеронимо) Кардано (1501–1576) ознакомился с методом Тартальи, но поклялся его не разглашать. Однако, в 1545 году вышла книга Кардано «Великое Искусство» («Ars Magna»), в которой он приводит методы решения уравнений третьей степени (формулы дель Ферро− Тартальи) и четвертой степени (метод Людовико Феррари (1522–1565), ученика Кардано).
Как Тарталья, так и Кардано столкнулись с трудностью, которую они так и не смогли разрешить: когда величина 
Этот случай Тарталья назвал «неприводимым». Кардано, решая задачу о нахождении сторон прямоугольного участка с площадью 40 и периметром 20 , пришел к системе


Кардано назвал 
Первая догадка, как из этих «софистических чисел»
получить действительные корни, пришла замечательному ученому из Болоньи Рафаэлю Бомбелли (1530–1572), который в своем труде «Алгебра» (1572) показал, что новые числа дают при извлечении квадратного корня сопряженные числа, при сложении которых взаимно уничтожается корень квадратный из отрицательного числа.
В этой же книге Бомбелли установил четыре правила действий над новыми числами и четыре правила, связывающие «новую» (
Именно поэтому Рафаэля Бомбелли считают основоположником теории комплексных чисел.
В дальнейшем комплексные числа встречаются в работах французского математика XVII века Рене Декарта (1596–1650) при исследовании решений алгебраических уравнений второй степени. В приложении к труду «Рассуждение о Методе, чтобы направлять свой разум и отыскивать истину в науках» (1637), называемом «Геометрия» (в третьей книге − «О природе уравнений») Декарт ставит вопрос: сколько корней может иметь алгебраическое уравнение n-й степени, и дает ответ: столько же, сколько имеет единиц степень уравнения. При этом он отмечает, что надо различать «истинные» (положительные), «ложные» (отрицательные) и «воображаемые» (мнимые) корни, подчеркивая, что линии на плоскости, которые не могут пересекаться при их алгебраическом представлении в виде уравнений, дают мнимые точки пересечения.
Однако, «мнимые» величины, выдвинутые Декартом и его последователями, долго не получали признания. Даже такой выдающийся математик и философ, как , писал: «Мнимые числа − это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием».
Первая удачная попытка геометрической интерпретации комплексных чисел была предпринята датским землемером и математиком Каспаром Весселем () в работе «Опыт аналитического представления направлений» (1797), которая, к сожалению, в течение столетия оставалась неизвестной.
После Весселя свою интерпретацию комплексных чисел предложил французский математик Жан Арган () в работе «Опыт некоторого представления мнимых количеств в геометрических построениях» (1806).
Однако, самую наглядную геометрическую интерпретацию комплексных чисел дал немецкий ученый, «король математиков» (1777–1855) в работе «Теория биквадратных вычетов» (1799) и позднее в «Арифметической теории комплексных чисел» (1806, 1825 и 1831), где он, рассматривая способ интерпретации новых чисел, назвал их впервые «комплексными числами» (от латинского слова «соmplex» — «объединение»), имея в виду объединение двух единиц (1 и 
(где а и b — действительные числа), оставив при этом идущее от Декарта название вторых единиц − «мнимые единицы».
В этой работе Гаусс навсегда изгнал таинственность, окружавшую мнимые числа, представив их с помощью точек плоскости. Позднее французский математик Огюстен Коши (1789–1857) в своем труде «Алгебраический анализ» (1821) продолжил эту удачную интерпретацию и ввел понятие модуля комплексного числа z = а + bi в виде неотрицательного действительного числа

1. , , Мордкович вопросы математики. 10 класс. Факультативный курс.– М.: Просвещение, 1980.
2. , , Шабунин и начала анализа. Пробный учебник 9-10 классов средней школы.– М. Просвещение, 1975.
3. Андронов действительных и комплексных чисел. – М.: Просвещение, 1975.
4. , , Пасиченко по математике. Алгебра. Справочное пособие. – М.: Наука, 1987.
5. , , Ашкенузе . Учебное пособие для 9-10 классов средней школы с математической специализацией. – М.: Просвещение, 1972.
6. , Ивашев-, Шварцбурд и математический анализ. Учебное пособие для учащихся 10 классов с углубленным изучением математики. – М.: Просвещение, 1989.
7. , , Шварцбурд изучение курса алгебры и математического анализа. – М.: Просвещение, 1991.
8. Гибш . Пособие для учителей 9−11 классов. – М.: Просвещение,1960.
9. , Солодовников – практикум по высшей алгебре для студентов−заочников физико-математических факультетов педагогических институтов. – М.: Просвещение, 1969.
10. , Новик и начала анализа. – М.: Просвещение, 1987.
11. Калнин и элементарные функции. – М.: Наука, 1964.
12. , , Яковлев и начала анализа. Часть II. Математика для техникумов. – М.: Наука, 1978.
13. Киселев . Часть II. Учебник для 8-10 классов средней школы. – М.: Учпедгиз, 1950.
14. Кочетков B. C., Кочеткова и элементарные функции. Часть II. – М.: Просвещение, 1968.
15. Крамор B. C. Алгебра и начала анализа. – М.: Высшая школа, 1981.
16. , , Яковлева по математике для поступающих в вузы. – М.: Наука, 1985.
17. Ларичев задач по алгебре. Часть II. Для 9−10 классов средней школы. – М.: Просвещение, 1965.
18. Математика в школе. № 3, 1990.
19. Математика в школе. № 6, 1992.
20. Окунев алгебра. – М.: Просвещение, 1966.
21. Петраков кружки в классах. – М.: Просвещение, 1988.
22. Петраков алгебры в педучилищах. Из опыта работы. – М.: Просвещение, 1970.
23. Понтрягин чисел. – М.: Просвещение, 1985.
24. Туманов математика. Пособие для самообразования. – М.: Просвещение, 1970.
25. , Соминский для самообразования. – М.: Наука, 1966.
26. , Пинский по методам решения задач по математике для средней школы. – М.: Наука. 1989.
27. Энциклопедический словарь юного математика. Составитель – М.: Педагогика, 1989.
28. Энциклопедия элементарной математики. Арифметика. Книга I. Под ред. – М.−Л.: Гостехиздат, 1951.
Комплексные числа и их приложение к решению
уравнений 3-й и 4-й степени
Глава 1. Комплексные числа в алгебраической
Занятие 1. Введение понятия комплексного числа.
Сложение, вычитание, умножение и
деление комплексных чисел.
Степени мнимой единицы (лекция) 6
Занятие 2. Операция сопряжения и ее свойства.
Модуль комплексного числа.
Извлечение корня квадратного
из комплексного числа (лекция) 15
Занятие 3. Действия с комплексными числами
в алгебраической форме (практика) 21 Занятие 4. Действия с комплексными числами
в алгебраической форме (практика) 27
Занятие 5. Контрольная работа №1 29
Глава 2. Геометрическая интерпретация
Занятие 6. Геометрическая интерпретация
комплексных чисел (лекция) 30
Занятия 7–8. Геометрическая интерпретация
комплексных чисел (практика) 33
Занятие 9. Контрольная работа №2 (45 мин.) 44
Глава 3. Комплексные числа в тригонометрической
Занятие 10. Тригонометрическая форма
комплексного числа, ее связь с
алгебраической формой (лекция) 45
Занятие 11. Действия с комплексными числами
в тригонометрической форме.
Возведение в натуральную степень
и извлечение корня из комплексного
числа в тригонометрической форме
(лекция) 50 Занятия 12–13. Действия с комплексными числами
в тригонометрической форме
Занятие 14. Контрольная работа №3 64
Глава 3. Решение уравнений 3-й и 4-й степени
Занятие 15. Решение уравнений третьей
степени (лекция) 65
Занятие 16. Решение уравнений третьей
степени (практика) 73
Занятие 17. Решение уравнений четвертой
степени методом Феррари (практика) 78
Из истории возникновения и развития понятия
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-chetvertoj-stepeni/
http://pandia.ru/text/78/443/83399-5.php