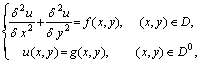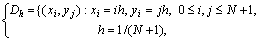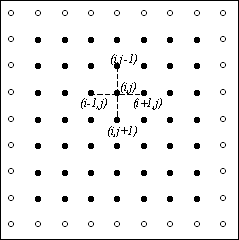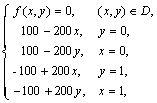Примеры решения задачи дирихле для уравнения

Дифференциальные уравнения в частных производных представляют собой широко применяемый математический аппарат при разработке моделей в самых разных областях науки и техники. К сожалению, явное решение этих уравнений в аналитическом виде оказывается возможным только в частных простых случаях, и, как результат, возможность анализа математических моделей, построенных на основе дифференциальных уравнений, обеспечивается при помощи приближенных численных методов решения. Объем выполняемых при этом вычислений обычно является значительным и использование высокопроизводительных вычислительных систем является традиционным для данной области вычислительной математики. Проблематика численного решения дифференциальных уравнений в частных производных является областью интенсивных исследований (см., например, [5,11,19]).

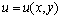
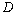
Рассмотрим в качестве учебного примера проблему численного решения задачи Дирихле для уравнения Пуассона, определяемую как задачу нахождения функции , удовлетворяющей в области определения уравнению

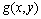
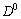
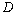
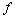
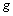
и принимающей значения на границе области ( и являются функциями, задаваемыми при постановке задачи). Подобная модель может быть использована для описания установившегося течения жидкости, стационарных тепловых полей, процессов теплопередачи с внутренними источниками тепла и деформации упругих пластин и др. Данный пример часто используется в качестве учебно-практической задачи при изложении возможных способов организации эффективных параллельных вычислений [4, 10, 27].

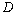
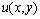
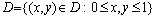
Для простоты изложения материала в качестве области задания функции далее будет использоваться единичный квадрат

6.1. Последовательные методы решения задачи Дирихле

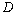
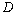
Одним из наиболее распространенных подходов численного решения дифференциальных уравнений является метод конечных разностей (метод сеток) [5,11]. Следуя этому подходу, область решения представляется в виде дискретного (как правило, равномерного) набора (сетки) точек (узлов). Так, например, прямоугольная сетка в области может быть задана в виде (рис. 6.1)

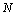
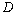
где величина задает количество узлов по каждой из координат области .

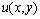
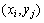
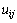
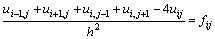
Обозначим оцениваемую при подобном дискретном представлении аппроксимацию функции в точках через . Тогда, используя пятиточечный шаблон (см. рис. 6.1) для вычисления значений производных, уравнение Пуассона может быть представлено в конечно-разностной форме

Данное уравнение может быть разрешено относительно

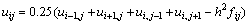
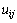
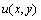
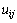
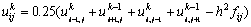
Разностное уравнение, записанное в подобной форме, позволяет определять значение по известным значениям функции в соседних узлах используемого шаблона. Данный результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений , а затем эти значения последовательно уточняются в соответствии с приведенным соотношением. Так, например, метод Гаусса-Зейделя для проведения итераций уточнения использует правило

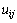
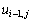
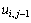
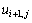
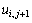
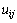
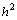
по которому очередное k-ое приближение значения вычисляется по последнему k-ому приближению значений и и предпоследнему (k-1)-ому приближению значений и . Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений не станут меньше некоторой заданной величины (требуемой точности вычислений). Сходимость описанной процедуры (получение решения с любой желаемой точностью) является предметом всестороннего математического анализа (см., например, [5,11]), здесь же отметим, что последовательность решений, получаемых методом сеток, равномерно сходится к решению задачи Дирихле, а погрешность решения имеет порядок .

Рис. 6.1. Прямоугольная сетка в области D (темные точки представляют внутренние узлы сетки, нумерация узлов в строках слева направо, а в столбцах — сверху вниз).

Рассмотренный алгоритм (метод Гаусса-Зейделя) на псевдокоде, приближенного к алгоритмическому языку С++, может быть представлен в виде:

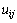
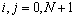
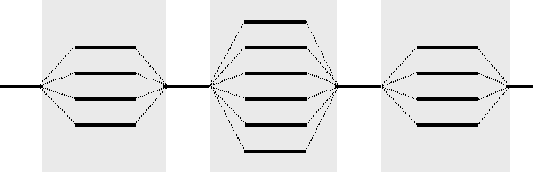
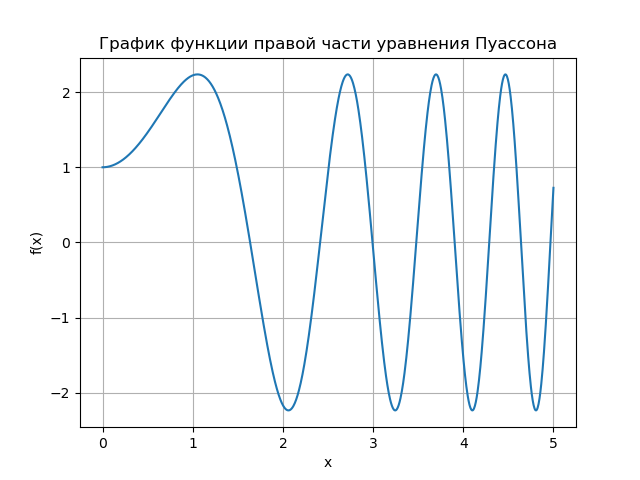
(напомним, что значения при индексах являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).

Рис. 6.2. Вид функции 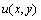в примере для задачи Дирихле

Для примера на рис. 6.2 приведен вид функции 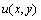, полученной для задачи Дирихле при следующих граничный условиях:

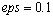
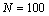
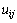
Общее количество итераций метода Гаусса-Зейделя составило 210 при точности решения и (в качестве начального приближения величин использовались значения, сгенерированные датчиком случайных чисел из диапазона [-100,100]).

6.2. Организация параллельных вычислений для систем с общей памятью

Как следует из приведенного описания, сеточные методы характеризуются значительной вычислительной трудоемкостью

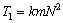
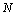
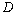
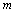
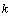
где есть количество узлов по каждой из координат области , — число операций, выполняемых методом для одного узла сетки, — количество итераций метода до выполнения условия остановки.

Использование OpenMP для организации параллелизма

Рассмотрим возможные способы организации параллельных вычислений для сеточных методов на многопроцессорных вычислительных системах с общей памятью. При изложении материала будем предполагать, что имеющие в составе системы процессоры обладают равной производительностью, являются равноправными при доступе к общей памяти и время доступа к памяти является одинаковым (при одновременном доступе нескольких процессоров к одному и тому же элементу памяти очередность и синхронизация доступа обеспечивается на аппаратном уровне). Многопроцессорные системы подобного типа обычно именуются симметричными мультипроцессорами (symmetric multiprocessors, SMP).

Обычный подход организации вычислений для подобных систем – создание новых параллельных методов на основе обычных последовательных программ, в которых или автоматически компилятором, или непосредственно программистом выделяются участки не зависимых друг от друга вычислений. Возможности автоматического анализа программ для порождения параллельных вычислений достаточно ограничены, и второй подход является преобладающим. При этом для разработки параллельных программ могут применяться как новые алгоритмические языки, ориентированные на параллельное программирование, так и уже имеющиеся языки программирования, расширенные некоторым набором операторов для параллельных вычислений.

Оба перечисленных подхода приводят к необходимости значительной переработки существующего программного обеспечения, и это в значительной степени затрудняет широкое распространение параллельных вычислений. Как результат, в последнее время активно развивается еще один подход к разработке параллельных программ, когда указания программиста по организации параллельных вычислений добавляются в программу при помощи тех или иных внеязыковых средств языка программирования – например, в виде директив или комментариев, которые обрабатываются специальным препроцессором до начала компиляции программы. При этом исходный операторный текст программы остается неизменным, по которому в случае отсутствия препроцессора компилятор построит исходный последовательный программный код. Препроцессор же, будучи примененным, заменяет директивы параллелизма на некоторый дополнительный программный код (как правило, в виде обращений к процедурам какой-либо параллельной библиотеки).

Рассмотренный выше подход является основой технологии OpenMP [17], наиболее широко применяемой в настоящее время для организации параллельных вычислений на многопроцессорных системах с общей памятью. В рамках данной технологии директивы параллелизма используются для выделения в программе параллельных областей (parallel regions), в которых последовательный исполняемый код может быть разделен на несколько раздельных командных потоков (threads). Далее эти потоки могут исполняться на разных процессорах вычислительной системы. В результате такого подхода программа представляется в виде набора последовательных (однопотоковых) и параллельных (многопотоковых) участков программного кода (см. рис. 6.3). Подобный принцип организации параллелизма получил наименование «вилочного» (fork-join) или пульсирующего параллелизма. Более полная информация по технологии OpenMP может быть получена, например, в [30] или в информационных ресурсах сети Интернет; в пособии возможности OpenMP будут излагаться в объеме, необходимом для демонстрации возможных способов разработки параллельных программ для рассматриваемого учебного примера решения задачи Дирихле.

Проблема синхронизации параллельных вычислений

Первый вариант параллельного алгоритма для метод сеток может быть получен, если разрешить произвольный порядок пересчета значений 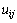. Программа для данного способа вычислений может быть представлена в следующем виде:

Следует отметить, что программа получена из исходного последовательного кода путем добавления директив и операторов обращения к функциям библиотеки OpenMP (эти дополнительные строки в программе выделены темным шрифтом, обратная наклонная черта в конце директив означает продолжение директив на следующих строках программы).

Рис. 6.3. Параллельные области, создаваемые директивами OpenMP

Как следует из текста программы, параллельные области в данном примере задаются директивой parallel for, являются вложенными и включают в свой состав операторы цикла for. Компилятор, поддерживающий технологию OpenMP, разделяет выполнение итераций цикла между несколькими потоками программы, количество которых обычно совпадает с числом процессоров в вычислительной системе. Параметры директивы shared и private определяют доступность данных в потоках программы – переменные, описанные как shared, являются общими для потоков, для переменных с описанием private создаются отдельные копии для каждого потока, которые могут использоваться в потоках независимо друг от друга.

Наличие общих данных обеспечивает возможность взаимодействия потоков. В этом плане, разделяемые переменные могут рассматриваться как общие ресурсы потоков и, как результат, их использование должно выполняться с соблюдением правил взаимоисключения (изменение каким-либо потоком значений общих переменных должно приводить к блокировке доступа к модифицируемым данным для всех остальных потоков). В данном примере таким разделяемым ресурсом является величина dmax, доступ потоков к которой регулируется специальной служебной переменной (семафором) dmax_lock и функциями omp_set_lock (разрешение или блокировка доступа) и omp_unset_lock (снятие запрета на доступ). Подобная организация программы гарантирует единственность доступа потоков для изменения разделяемых данных; как отмечалось ранее, участки программного кода (блоки между обращениями к функциям omp_set_lock и omp_unset_lock), для которых обеспечивается взаимоисключение, обычно именуются критическими секциями.

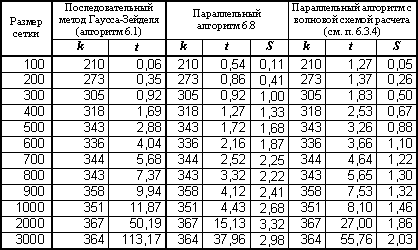
Результаты вычислительных экспериментов приведены в табл. 6.1 (здесь и далее для параллельных программ, разработанных с использованием технологии OpenMP, использовался четырехпроцессорный сервер кластера Нижегородского университета с процессорами Pentium III, 700 Mhz, 512 RAM).

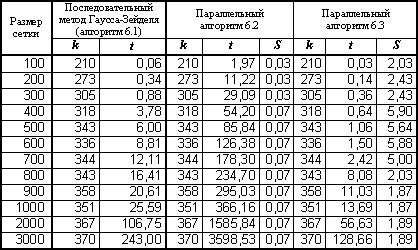
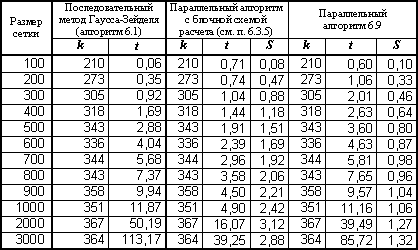
Таблица 6.1. Результаты вычислительных экспериментов для параллельных вариантов алгоритма Гаусса-Зейделя (p=4)

(k – количество итераций, t– время в сек., S – ускорение)

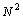
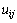
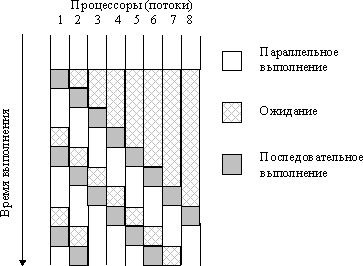
Оценим полученный результат. Разработанный параллельный алгоритм является корректным, т.е. обеспечивающим решение поставленной задачи. Использованный при разработке подход обеспечивает достижение практически максимально возможного параллелизма – для выполнения программы может быть задействовано вплоть до процессоров. Тем не менее результат не может быть признан удовлетворительным – программа будет работать медленно и ускорение вычислений от использования нескольких процессоров окажется не столь существенным. Основная причина такого положения дел – чрезмерно высокая синхронизация параллельных участков программы. В нашем примере каждый параллельный поток после усреднения значений должен проверить (и возможно изменить) значение величины dmax. Разрешение на использование переменной может получить только один поток – все остальные

Рис. 6.4. Пример возможной схемы выполнения параллельных потоков при наличии синхронизации (взаимоисключения)

потоки должны быть блокированы. После освобождения общей переменной управление может получить следующий поток и т.д. В результате необходимости синхронизации доступа многопотоковая параллельная программа превращается фактически в последовательно выполняемый код, причем менее эффективный, чем исходный последовательный вариант, т.к. организация синхронизации приводит к дополнительным вычислительным затратам – см. рис. 6.4. Следует обратить внимание, что, несмотря на идеальное распределение вычислительной нагрузки между процессорами, для приведенного на рис. 6.4 соотношения параллельных и последовательных вычислений, в каждый текущий момент времени (после момента первой синхронизации) только не более двух процессоров одновременно выполняют действия, связанные с решением задачи. Подобный эффект вырождения параллелизма из-за интенсивной синхронизации параллельных участков программы обычно именуются сериализацией (serialization).

Как показывают выполненные рассуждения, путь для достижения эффективности параллельных вычислений лежит в уменьшении необходимых моментов синхронизации параллельных участков программы. Так, в нашем примере мы можем ограничиться распараллеливанием только одного внешнего цикла for. Кроме того, для снижения количества возможных блокировок применим для оценки максимальной погрешности многоуровневую схему расчета: пусть параллельно выполняемый поток первоначально формирует локальную оценку погрешности dm только для своих обрабатываемых данных (одной или нескольких строк сетки), затем при завершении вычислений поток сравнивает свою оценку dm с общей оценкой погрешности dmax.

Новый вариант программы решения задачи Дирихле имеет вид:

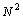
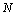
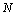
Как результат выполненного изменения схемы вычислений, количество обращений к общей переменной dmax уменьшается с до раз, что должно приводить к существенному снижению затрат на синхронизацию потоков и уменьшению проявления эффекта сериализации вычислений. Результаты экспериментов с данным вариантом параллельного алгоритма, приведенные в табл. 6.1, показывают существенное изменение ситуации – ускорение в ряде экспериментов оказывается даже большим, чем используемое количество процессоров (такой эффект сверхлинейного ускорения достигается за счет наличия у каждого из процессоров вычислительного сервера своей быстрой кэш памяти). Следует также обратить внимание, что улучшение показателей параллельного алгоритма достигнуто при снижении максимально возможного параллелизма (для выполнения программы может использоваться не более процессоров).

Возможность неоднозначности вычислений в параллельных программах

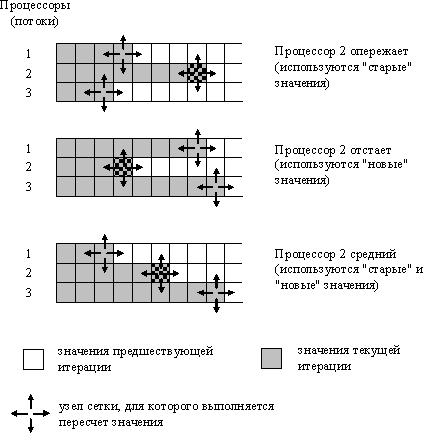
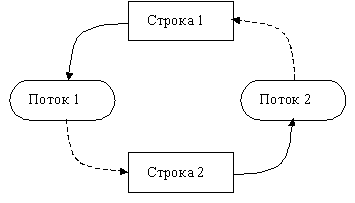
Последний рассмотренный вариант организации параллельных вычислений для метода сеток обеспечивает практически максимально возможное ускорение выполняемых расчетов – так, в экспериментах данное ускорение достигало величины 5.9 при использовании четырехпроцессорного вычислительного сервера. Вместе с этим необходимо отметить, что разработанная вычислительная схема расчетов имеет важную принципиальную особенность – порождаемая при вычислениях последовательность обработки данных может различаться при разных запусках программы даже при одних и тех же исходных параметрах решаемой задачи. Данный эффект может проявляться в силу изменения каких-либо условий выполнения программы (вычислительной нагрузки, алгоритмов синхронизации потоков и т.п.), что может повлиять на временные соотношения между потоками (см. рис. 6.5). Взаиморасположение потоков по области расчетов может быть различным: одни потоки могут опережать другие и, обратно, часть потоков могут отставать (при этом, характер взаиморасположения может меняться в ходе вычислений). Подобное поведение параллельных участков программы обычно именуется состязанием потоков (race condition) и отражает важный принцип параллельного программирования – временная динамика выполнения параллельных потоков не должна учитываться при разработке параллельных алгоритмов и программ.

Рис. 6.5. Возможные различные варианты взаиморасположения параллельных потоков (состязание потоков)

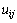
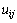
В рассматриваемом примере при вычислении нового значения в зависимости от условий выполнения могут использоваться разные (от предыдущей или текущей итераций) оценки соседних значений по вертикали. Тем самым, количество итераций метода до выполнения условия остановки и, самое главное, конечное решение задачи может различаться при повторных запусках программы. Получаемые оценки величин будут соответствовать точному решению задачи в пределах задаваемой точности, но, тем не менее, могут быть различными. Использование вычислений такого типа для сеточных алгоритмов получило наименование метода хаотической релаксации (chaotic relaxation).

Проблема взаимоблокировки

Возможный подход для получения однозначных результатов (уход от состязания потоков) может состоять в ограничении доступа к узлам сетки, которые обрабатываются в параллельных потоках программы. Для этого можно ввести набор семафоров row_lock[N], который позволит потокам закрывать доступ к «своим» строкам сетки:

Закрыв доступ к своим данным, параллельный поток уже не будет зависеть от динамики выполнения других параллельных участков программы. Результат вычислений потока однозначно определяется значениями данных в момент начала расчетов.

Данный подход позволяет продемонстрировать еще одну проблему, которая может возникать в ходе параллельных вычислений. Эта проблема состоит в том, что при организации доступа к множественным общим переменным может возникать конфликт между параллельными потоками и этот конфликт не может быть разрешен успешно. Так, в приведенном фрагменте программного кода при обработке потоками двух последовательных строк (например, строк 1 и 2) может сложиться ситуация, когда потоки блокируют сначала строки 1 и 2 и только затем переходят к блокировке оставшихся строк (см. рис. 6.6). В этом случае доступ к необходимым строкам не может быть обеспечен ни для одного потока – возникает неразрешимая ситуация, обычно именуемая тупиком. Как отмечалось в главе 5 пособия, необходимым условием тупика является наличие цикла в графе распределения и запросов ресурсов. В рассматриваемом примере уход от цикла может состоять в строго последовательной схеме блокировки строк потока

(следует отметить, что и эта схема блокировки строк может оказаться тупиковой, если рассматривать модифицированную задачу Дирихле, в которой горизонтальные границы являются «склеенными»).

Рис. 6.6. Ситуация тупика при доступе к строкам сетки (поток 1 владеет строкой 1 и запрашивает строку 2, поток 2 владеет строкой 2 и запрашивает строку 1)

Исключение неоднозначности вычислений

Подход, рассмотренный в п. 4, уменьшает эффект состязания потоков, но не гарантирует единственности решения при повторении вычислений. Для достижения однозначности необходимо использование дополнительных вычислительных схем.

Возможный и широко применяемый в практике расчетов способ состоит в разделении места хранения результатов вычислений на предыдущей и текущей итерациях метода сеток. Схема такого подхода может быть представлена в следующем общем виде:

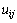
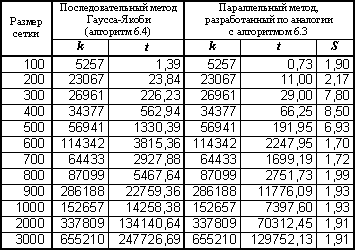
Как следует из приведенного алгоритма, результаты предыдущей итерации запоминаются в массиве u, новые вычисления значения запоминаются в дополнительном массиве un. Как результат, независимо от порядка выполнения вычислений для проведения расчетов всегда используются значения величин от предыдущей итерации метода. Такая схема реализация сеточных алгоритмов обычно именуется методом Гаусса-Якоби. Этот метод гарантирует однозначность результаты независимо от способа распараллеливания, но требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса-Зейделя) скоростью сходимости. Результаты расчетов с последовательным и параллельным вариантами метода приведены в табл. 6.2.

Таблица 6.2. Результаты вычислительных экспериментов
для алгоритма Гаусса-Якоби (p=4)

(k – количество итераций, t – время в сек., S – ускорение)

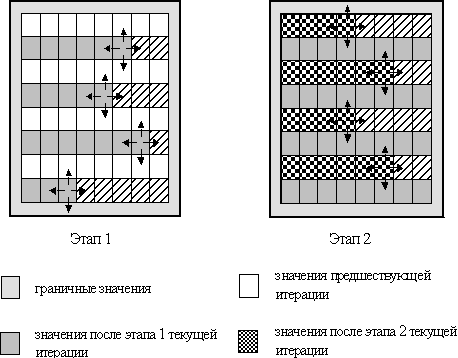
Иной возможный подход для устранения взаимозависимости параллельных потоков состоит в применении схемы чередования обработки четных и нечетных строк (red/black row alternation scheme), когда выполнение итерации метода сеток подразделяется на два последовательных этапа, на первом из которых обрабатываются строки только с четными номерами, а затем на втором этапе — строки с нечетными номерами (см. рис. 6.7). Данная схема может быть обобщена на применение одновременно и к строкам, и к столбцам (шахматное разбиение) области расчетов.

Рассмотренная схема чередования строк не требует по сравнению с методом Якоби какой-либо дополнительной памяти и обеспечивает однозначность решения при многократных запусках программы. Но следует заметить, что оба рассмотренных в данном пункте подхода могут получать результаты, не совпадающие с решением задачи Дирихле, найденном при помощи последовательного алгоритма. Кроме того, эти вычислительные схемы имеют меньшую область и худшую скорость сходимости, чем исходный вариант метода Гаусса-Зейделя.

Рис. 6.7. Схема чередования обработки четных и нечетных строк

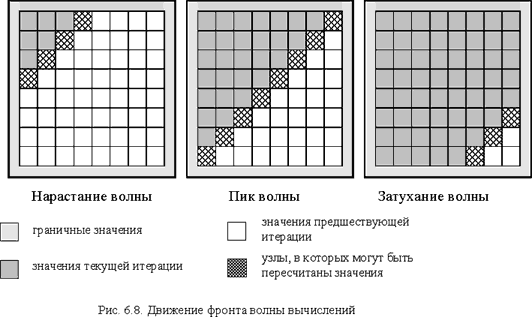
Волновые схемы параллельных вычислений

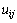
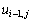
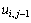
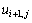
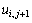
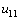
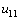
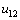
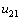
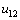
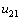
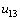
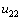
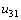
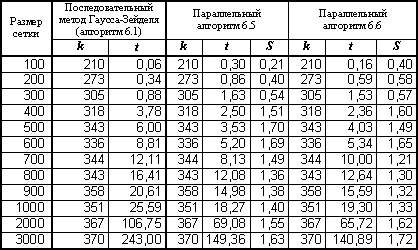
Рассмотрим теперь возможность построения параллельного алгоритма, который выполнял бы только те вычислительные действия, что и последовательный метод (может быть только в некотором ином порядке) и, как результат, обеспечивал бы получение точно таких же решений исходной вычислительной задачи. Как уже было отмечено выше, в последовательном алгоритме каждое очередное k-ое приближение значения вычисляется по последнему k-ому приближению значений и и предпоследнему (k-1)-ому приближению значений и . Как результат, при требовании совпадения результатов вычислений последовательных и параллельных вычислительных схем в начале каждой итерации метода только одно значение может быть пересчитано (возможности для распараллеливания нет). Но далее после пересчета вычисления могут выполняться уже в двух узлах сетки и (в этих узлах выполняются условия последовательной схемы), затем после пересчета узлов и — в узлах , и и т.д. Обобщая сказанное, можно увидеть, что выполнение итерации метода сеток можно разбить на последовательность шагов, на каждом из которых к вычислениям окажутся подготовленными узлы вспомогательной диагонали сетки с номером, определяемом номером этапа – см. рис. 6.8. Получаемая в результате вычислительная схема получила наименование волны или фронта вычислений, а алгоритмы, получаемые на ее основе, — методами волновой обработки данных (wavefront or hyperplane methods). Следует отметить, что в нашем случае размер волны (степень возможного параллелизма) динамически изменяется в ходе вычислений – волна нарастает до своего пика, а затем затухает при приближении к правому нижнему узлу сетки.

Таблица 6.3. Результаты экспериментов для параллельных вариантов алгоритма Гаусса-Зейделя с волновой схемой расчета (p=4)

(k – количество итераций, t – время в сек., S – ускорение)

Возможная схема параллельного метода, основанного на эффекте волны вычислений, может быть представлена в следующей форме:

При разработки алгоритма, реализующего волновую схему вычислений, оценку погрешности решения можно осуществлять для каждой строки в отдельности (массиы значений dm). Этот массив является общим для всех выполняемых потоков, однако, синхронизации доступа к элементам не требуется, так как потоки используют всегда разные элементы массива (фронт волны вычислений содержит только по одному узлу строк сетки).

После обработки всех элементов волны среди массива dm находится максимальная погрешность выполненной итерации вычислений. Однако именно эта последняя часть расчетов может оказаться наиболее неэффективной из-за высоких дополнительных затрат на синхронизацию. Улучшение ситуации, как и ранее, может быть достигнуто за счет увеличения размера последовательных участков и сокращения, тем самым, количества необходимых взаимодействий параллельных участков вычислений. Возможный вариант реализации такого подхода может состоять в следующем:

Подобный прием укрупнения последовательных участков вычислений для снижения затрат на синхронизацию именуется фрагментированием (chunking). Результаты экспериментов для данного варианта параллельных вычислений приведены в табл. 6.3.

Следует обратить внимание на еще один момент при анализе эффективности разработанного параллельного алгоритма. Фронт волны вычислений плохо соответствует правилам использования кэша — быстродействующей дополнительной памяти компьютера, используемой для хранения копии наиболее часто используемых областей оперативной памяти. Использование кэша может существенно повысить (в десятки раз) быстродействие вычислений. Размещение данных в кэше может происходить или предварительно (при использовании тех или иных алгоритмов предсказания потребности в данных) или в момент извлечения значений из основной оперативной памяти. При этом подкачка данных в кэш осуществляется не одиночными значениями, а небольшими группами – строками кэша (cache line). Загрузка значений в строку кэша осуществляется из последовательных элементов памяти; типовые размеры строки кэша обычно равны 32, 64, 128, 256 байтам (дополнительная информация по организации памяти может быть получена, например, в [12]). Как результат, эффект наличия кэша будет наблюдаться, если выполняемые вычисления используют одни и те же данные многократно (локальность обработки данных) и осуществляют доступ к элементам памяти с последовательно возрастающими адресами (последовательность доступа).

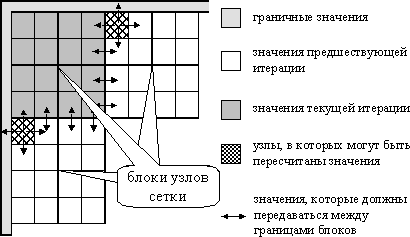
В рассматриваемом нами алгоритме размещение данных в памяти осуществляется по строкам, а фронт волны вычислений располагается по диагонали сетки, и это приводит к низкой эффективности использования кэша. Возможный способ улучшения ситуации – опять же укрупнение вычислительных операций и рассмотрение в качестве распределяемых между процессорами действий процедуру обработки некоторой прямоугольной подобласти (блока) сетки области расчетов — см. рис. 6.9.

Рис. 6.9. Блочное представление сетки области расчетов

Порождаемый на основе такого подхода метод вычислений в самом общем виде может быть описан следующим образом (блоки образуют в области расчётов прямоугольную решётку размера NBxNB):

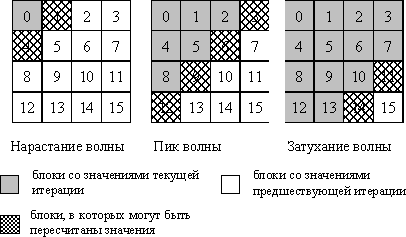
Вычисления в предлагаемом алгоритме происходят в соответствии с волновой схемой обработки данных – вначале вычисления выполняются только в левом верхнем блоке с координатами (0,0), далее для обработки становятся доступными блоки с координатами (0,1) и (1,0) и т.д. – см. результаты экспериментов в табл. 6.3.

Блочный подход к методу волновой обработки данных существенным образом меняет состояние дел – обработку узлов можно организовать построчно, доступ к данным осуществляется последовательно по элементам памяти, перемещенные в кэш значения используются многократно. Кроме того, поскольку обработка блоков будет выполняться на разных процессорах и блоки не пересекаются по данным, при таком подходе будут отсутствовать и накладные расходы для обеспечения однозначности (когерентности) кэшей разных процессоров.

Наилучшие показатели использования кэша будут достигаться, если в кэше будет достаточно места для размещения не менее трех строк блока (при обработке строки блоки блока используются данные трех строк блока одновременно). Тем самым, исходя из размера кэша, можно определить рекомендуемый максимально-возможный размер блока. Так, например, при кэше 8 Кб и 8-байтовых значениях данных этот размер составит приближенно 300 (8Кб/3/8). Можно определить и минимально-допустимый размер блока из условия совпадения размеров строк кэша и блока. Так, при размере строки кэша 256 байт и 8-байтовых значениях данных размер блока должен быть кратен 32.

Последнее замечание следует сделать о взаимодействии граничных узлов блоков. Учитывая граничное взаимодействие, соседние блоки целесообразно обрабатывать на одних и тех же процессорах. В противном случае, можно попытаться так определить размеры блоков, чтобы объем пересылаемых между процессорами граничных данных был минимален. Так, при размере строки кэша в 256 байт, 8-байтовых значениях данных и размере блока 64х64 объем пересылаемых данных 132 строки кэша, при размере блока 128х32 – всего 72 строки. Такая оптимизация имеет наиболее принципиальное значение при медленных операциях пересылки данных между кэшами процессоров, т.е. для систем с неоднородным доступом к памяти, (nonuniform memory access — NUMA).

Балансировка вычислительной нагрузки процессоров

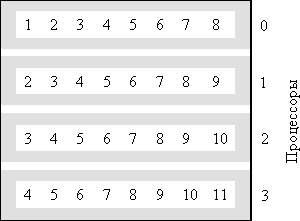
Как уже отмечалось ранее, вычислительная нагрузка при волновой обработке данных изменяется динамически в ходе вычислений. Данный момент следует учитывать при распределении вычислительной нагрузки между процессорами. Так, например, при фронте волны из 5 блоков и при использовании 4 процессоров обработка волны потребует двух параллельных итераций, во время второй из которых будет задействован только один процессор, а все остальные процессоры будут простаивать, дожидаясь завершения вычислений. Достигнутое ускорение расчетов в этом случае окажется равным 2.5 вместо потенциально возможного значения 4. Подобное снижение эффективности использования процессоров становится менее заметным при большой длине волны, размер которой может регулироваться размером блока. Как общий результат, можно отметить, что размер блока определяет степень разбиения (granularity) вычислений для распараллеливания и является параметром, подбором значения для которого можно управлять эффективностью параллельных вычислений.

Для обеспечения равномерности (балансировки) загрузки процессоров можно задействовать еще один подход, широко используемый для организации параллельных вычислений. Этот подход состоит в том, что все готовые к выполнению в системе вычислительные действия организуются в виде очереди заданий. В ходе вычислений освободившийся процессор может запросить для себя работу из этой очереди; появляющиеся по мере обработки данных дополнительные задания пополняют задания очереди. Такая схема балансировки вычислительной нагрузки между процессорами является простой, наглядной и эффективной. Это позволяет говорить об использовании очереди заданий как об общей модели организации параллельных вычислений для систем с общей памятью.

Рассмотренная схема балансировки может быть задействована и для рассматриваемого учебного примера. На самом деле, в ходе обработки фронта текущей волны происходит постепенное формирование блоков следующей волны вычислений. Эти блоки могут быть задействованы для обработки при нехватке достаточной вычислительной нагрузки для процессоров

Общая схема вычислений с использованием очереди заданий может быть представлена в следующем виде:

Для описания имеющихся в задаче блоков узлов сетки в алгоритме используется структура со следующим набором параметров:

Lock – семафор, синхронизирующий доступ к описанию блока,
pNext – указатель на соседний справа блок,
pDown – указатель на соседний снизу блок,
Count – счетчик готовности блока к вычислениям (количество готовых границ блока).

Операции для выборки из очереди и вставки в очередь указателя на готовый к обработке блок узлов сетки обеспечивают соответственно функции GetBlock и PutBlock.

Как следует из приведенной схемы, процессор извлекает блок для обработки из очереди, выполняет необходимые вычисления для блока и отмечает готовность своих границ для соседних справа и снизу блоков. Если при этом оказывается, что у соседних блоков являются подготовленными обе границы, процессор передает эти блоки для запоминания в очередь заданий.

Использование очереди заданий позволяет решить практически все оставшиеся вопросы организации параллельных вычислений для систем с общей памятью. Развитие рассмотренного подхода может предусматривать уточнение правил выделения заданий из очереди для согласования с состояниями процессоров (близкие блоки целесообразно обрабатывать на одних и тех же процессорах), расширение числа имеющихся очередей заданий и т.п. Дополнительная информация по этим вопросам может быть получена, например, в [29, 31].

6.3. Организация параллельных вычислений для систем с распределенной памятью

Использование процессоров с распределенной памятью является другим общим способом построения многопроцессорных вычислительных систем. Актуальность таких систем становится все более высокой в последнее время в связи с широким развитием высокопроизводительных кластерных вычислительных систем (см. раздел 1 пособия).

Многие проблемы параллельного программирования (состязание вычислений, тупики, сериализация) являются общими для систем с общей и распределенной памятью. Момент, который отличает параллельные вычисления с распределенной памятью, состоит в том, что взаимодействие параллельных участков программы на разных процессорах может быть обеспечено только при помощи передачи сообщений (message passing).

Следует отметить, что процессор с распределенной памятью является, как правило, более сложным вычислительным устройством, чем процессор в многопроцессорной системе с общей памятью. Для учета этих различий в дальнейшем процессор с распределенной памятью будет именоваться как вычислительный сервер (сервером может быть, в частности, многопроцессорная система с общей памятью). При проведении всех ниже рассмотренных экспериментов использовались 4 компьютера с процессорами Pentium IV, 1300 Mhz, 256 RAM, 100 Mbit Fast Ethernet.

Разделение данных

Первая проблема, которую приходится решать при организации параллельных вычислений на системах с распределенной памяти, обычно состоит в выборе способа разделения обрабатываемых данных между вычислительными серверами. Успешность такого разделения определяется достигнутой степенью локализации вычислений на серверах (в силу больших временных задержек при передаче сообщений интенсивность взаимодействия серверов должна быть минимальной).

Рис. 6.10. Ленточное разделение области расчетов между процессорами (кружки представляют граничные узлы сетки)

В рассматриваемой учебной задаче по решению задачи Дирихле возможны два различных способа разделения данных – одномерная или ленточная схема (см. рис. 6.10) или двухмерное или блочное разбиение (см. рис. 6.9) вычислительной сетки. Дальнейшее изложение учебного материала будет проводиться на примере первого подхода; блочная схема будет рассмотрена позднее в более кратком виде.

Основной момент при организации вычислений с подобным разделением данных состоит в том, что на процессор, выполняющий обработку какой-либо полосы, должны быть продублированы граничные строки предшествующей и следующей полос вычислительной сетки (получаемые в результате расширенные полосы показаны на рис. 6.10 справа пунктирными рамками). Продублированные граничные строки полос используются только при проведении расчетов, пересчет же этих строк происходит в полосах своего исходного месторасположения. Тем самым дублирование граничных строк должно осуществляться перед началом выполнения каждой очередной итерации метода сеток.

Обмен информацией между процессорами

Параллельный вариант метода сеток при ленточном разделении данных состоит в обработке полос на всех имеющихся серверах одновременно в соответствии со следующей схемой работы:

ProcNum – номер процессора, на котором выполняются описываемые действия,
PrevProc, NextProc – номера соседних процессоров, содержащих предшествующую и следующую полосы,
NP – количество процессоров,
M – количество строк в полосе (без учета продублированных граничных строк),
N – количество внутренних узлов в строке сетки (т.е. всего в строке N+2 узла).

Для нумерации строк полосы будем использовать нумерацию, при которой строки 0 и M+1 есть продублированные из соседних полос граничные строки, а строки собственной полосы процессора имеют номера от 1 до M.

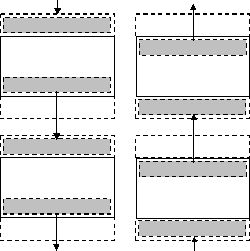
Рис. 6.11. Схема передачи граничных строк между соседними процессорами

Процедура обмена граничных строк между соседними процессорами может быть разделена на две последовательные операции, во время первой из которых каждый процессор передает свою нижнюю граничную строку следующему процессору и принимает такую же строку от предыдущего процессора (см. рис. 6.11). Вторая часть передачи строк выполняется в обратном направлении: процессоры передают свои верхние граничные строки своим предыдущим соседям и принимают переданные строки от следующих процессоров.

Выполнение подобных операций передачи данных в общем виде может быть представлено следующим образом (для краткости рассмотрим только первую часть процедуры обмена):

(для записи процедур приема-передачи используется близкий к стандарту MPI [20] формат, где первый и второй параметры представляют пересылаемые данные и их объем, а третий параметр определяет адресат (для операции Send) или источник (для операции Receive) пересылки данных).

Для передачи данных могут быть задействованы два различных механизма. При первом из них выполнение программ, инициировавших операцию передачи, приостанавливается до полного завершения всех действий по пересылке данных (т.е. до момента получения процессором-адресатом всех передаваемых ему данных). Операции приема-передачи, реализуемые подобным образом, обычно называются синхронными или блокирующими. Иной подход – асинхронная или неблокирующая передача — может состоять в том, что операции приема-передачи только инициируют процесс пересылки и на этом завершают свое выполнение. В результате программы, не дожидаясь завершения длительных коммуникационных операций, могут продолжать свои вычислительные действия, проверяя по мере необходимости готовность передаваемых данных. Оба эти варианта операций передачи широко используются при организации параллельных вычислений и имеют свои достоинства и свои недостатки. Синхронные процедуры передачи, как правило, более просты для использования и более надежны; неблокирующие операции могут позволить совместить процессы передачи данных и вычислений, но обычно приводят к повышению сложности программирования. С учетом всех последующих примеров для организации пересылки данных будут использоваться операции приема-передачи блокирующего типа.

Приведенная выше последовательность блокирующих операций приема-передачи данных (вначале Send, затем Receive) приводит к строго последовательной схеме выполнения процесса пересылок строк, т.к. все процессоры одновременно обращаются к операции Send и переходят в режим ожидания. Первым процессором, который окажется готовым к приему пересылаемых данных, окажется сервер с номером NP-1. В результате процессор NP-2 выполнит операцию передачи своей граничной строки и перейдет к приему строки от процессора NP-3 и т.д. Общее количество повторений таких операций равно NP-1. Аналогично происходит выполнение и второй части процедуры пересылки граничных строк перед началом обработки строк (см. рис. 6.11).

Последовательный характер рассмотренных операций пересылок данных определяется выбранным способом очередности выполнения. Изменим этот порядок очередности при помощи чередования приема и передачи для процессоров с четными и нечетными номерами:

Данный прием позволяет выполнить все необходимые операции передачи всего за два последовательных шага. На первом шаге все процессоры с нечетными номерами отправляют данные, а процессоры с четными номерами осуществляют прием этих данных. На втором шаге роли процессоров меняются – четные процессоры выполняют Send, нечетные процессоры исполняют операцию приема Receive.

Рассмотренные последовательности операций приема-передачи для взаимодействия соседних процессоров широко используются в практике параллельных вычислений. Как результат, во многих базовых библиотеках параллельных программ имеются процедуры для поддержки подобных действий. Так, в стандарте MPI [21] предусмотрена операция Sendrecv, с использованием которой предыдущий фрагмент программного кода может быть записан более кратко:

Реализация подобной объединенной функции Sendrecv обычно осуществляется таким образом, чтобы обеспечить и корректную работу на крайних процессорах, когда не нужно выполнять одну из операций передачи или приема, и организацию чередования процедур передачи на процессорах для ухода от тупиковых ситуаций и возможности параллельного выполнения всех необходимых пересылок данных.

Коллективные операции обмена информацией

Для завершения круга вопросов, связанных с параллельной реализацией метода сеток на системах с распределенной памятью, осталось рассмотреть способы вычисления общей для всех процессоров погрешности вычислений. Возможный очевидный подход состоит в передаче всех локальных оценок погрешности, полученный на отдельных полосах сетки, на один какой-либо процессор, вычисления на нем максимального значения и рассылки полученного значения всем процессорам системы. Однако такая схема является крайне неэффективной – количество необходимых операций передачи данных определяется числом процессоров и выполнение этих операций может происходить только в последовательном режиме. Между тем, как показывает анализ требуемых коммуникационных действий, выполнение операций сборки и рассылки данных может быть реализовано с использованием рассмотренной в п. 4.1 пособия каскадной схемы обработки данных. На самом деле, получение максимального значения локальных погрешностей, вычисленных на каждом процессоре, может быть обеспечено, например, путем предварительного нахождения максимальных значений для отдельных пар процессоров (данные вычисления могут выполняться параллельно), затем может быть снова осуществлен попарный поиск максимума среди полученных результатов и т.д. Всего, как полагается по каскадной схеме, необходимо выполнить log2NP параллельных итераций для получения конечного значения (NP – количество процессоров).

Учитывая большую эффективность каскадной схемы для выполнения коллективных операций передачи данных, большинство базовых библиотек параллельных программ содержит процедуры для поддержки подобных действий. Так, в стандарте MPI [21] предусмотрены операции:

Reduce(dm,dmax,op,proc) – процедура сборки на процессоре proc итогового результата dmax среди локальных на каждом процессоре значений dm с применением операции op,
Broadcast(dmax,proc) – процедура рассылки с процессора proc значения dmax всем имеющимся процессорам системы.

С учетом перечисленных процедур общая схема вычислений на каждом процессоре может быть представлена в следующем виде:

(в приведенном алгоритме переменная dm представляет локальную погрешность вычислений на отдельном процессоре, параметр MAX задает операцию поиска максимального значения для операции сборки). Следует отметить, что в составе MPI имеется процедура Allreduce, которая совмещает действия редукции и рассылки данных. Результаты экспериментов для данного варианта параллельных вычислений для метода Гаусса-Зейделя приведены в табл. 6.4.

Организация волны вычислений

Представленные в пп. 1-3 алгоритмы определяют общую схему параллельных вычислений для метода сеток в многопроцессорных системах с распределенной памятью. Далее эта схема может быть конкретизирована реализацией практически всех вариантов методов, рассмотренных для систем с общей памятью (использование дополнительной памяти для схемы Гаусса-Якоби, чередование обработки полос и т.п.). Проработка таких вариантов не привносит каких-либо новых эффектов с точки зрения параллельных вычислений и их разбор может использоваться как темы заданий для самостоятельных упражнений.

Таблица 6.4. Результаты экспериментов для систем с распределенной памятью, ленточная схема разделения данных (p=4)

(k – количество итераций, t – время в сек., S – ускорение)

В завершение рассмотрим возможность организации параллельных вычислений, при которых обеспечивалось бы нахождение таких же решений задачи Дирихле, что и при использовании исходного последовательного метода Гаусса-Зейделя. Как отмечалось ранее, такой результат может быть получен за счет организации волновой схемы расчетов. Для образования волны вычислений представим логически каждую полосу узлов области расчетов в виде набора блоков (размер блоков можно положить, в частности, равным ширине полосы) и организуем обработку полос поблочно в последовательном порядке (см. рис. 6.12). Тогда для полного повторения действий последовательного алгоритма вычисления могут быть начаты только для первого блока первой полосы узлов; после того, как этот блок будет обработан, для вычислений будут готовы уже два блока – блок 2 первой полосы и блок 1 второй полосы (для обработки блока полосы 2 необходимо передать граничную строку узлов первого блока полосы 1). После обработки указанных блоков к вычислениям будут готовы уже 3 блока и мы получаем знакомый уже процесс волновой обработки данных (результаты экспериментов см. в табл. 6.4).

Рис. 6.12. Организация волны вычислений при ленточной схеме разделения данных

Интересной момент при организации подобный схемы параллельных вычислений может состоять в попытке совмещения операций пересылки граничных строк и действий по обработке блоков данных.

Блочная схема разделения данных

Ленточная схема разделения данных может быть естественным образом обобщена на блочный способ представления сетки области расчетов (см. рис. 6.9). При этом столь радикальное изменение способа разбиения сетки практически не потребует каких-либо существенных корректировок рассмотренной схемы параллельных вычислений. Основной новый момент при блочном представлении данных состоит в увеличении количества граничных строк на каждом процессоре (для блока их количество становится равным 4), что приводит, соответственно, к большему числу операций передачи данных при обмене граничных строк. Сравнивая затраты на организацию передачи граничных строк, можно отметить, что при ленточной схеме для каждого процессора выполняется 4 операции приема-передачи данных, в каждой из которых пересылается (N+2) значения; для блочного же способа происходит 8 операций пересылки и объем каждого сообщения равен (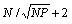) (N – количество внутренних узлов сетки, NP – число процессоров, размер всех блоков предполагается одинаковым). Тем самым, блочная схема представления области расчетов становится оправданной при большом количество узлов сетки области расчетов, когда увеличение количества коммуникационных операций приводит к снижению затрат на пересылку данных в силу сокращения размеров передаваемых сообщений. Результаты экспериментов при блочной схеме разделения данных приведены в табл. 6.5.

Таблица 6.5. Результаты экспериментов для систем с распределенной памятью, блочная схема разделения данных (p=4)

(k – количество итераций, t – время в сек., S – ускорение)

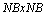
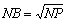
При блочном представлении сетки может быть реализован также и волновой метод выполнения расчетов (см. рис. 6.13). Пусть процессоры образуют прямоугольную решетку размером () и процессоры пронумерованы от 0 слева направо по строкам решетки.

Общая схема параллельных вычислений в этом случае имеет вид:

(в приведенном алгоритме функция Barrier() представляет операцию коллективной синхронизации, которая завершает свое выполнение только в тот момент, когда все процессоры осуществят вызов этой процедуры).

Следует обратить внимание, что при реализации алгоритма обеспечиться, чтобы в начальный момент времени все процессоры (кроме процессора с нулевым номером) оказались в состоянии передачи своих граничных узлов (верхней строки и левого столбца). Вычисления должен начинать процессор с левым верхним блоком, после завершения обработки которого обновленные значения правого столбца и нижней строки блока необходимо переправить правому и нижнему процессорам решетки соответственно. Данные действия обеспечат снятие блокировки процессоров второй диагонали процессорной решётки (ситуация слева на рис. 6.13) и т.д.

Анализ эффективности организации волновых вычислений в системах с распределенной памятью (см. табл. 6.5) показывает значительное снижение полезной вычислительной нагрузки для процессоров, которые занимаются обработкой данных только в моменты, когда их блоки попадают во фронт волны вычислений. При этом балансировка (перераспределение) нагрузки является крайне затруднительной, поскольку связана с пересылкой между процессорами блоков данных большого объема. Возможный интересный способ улучшения ситуации состоит в организации множественной волны вычислений, в соответствии с которой процессоры после отработки волны текущей итерации расчетов могут приступить к выполнению волны следующей итерации метода сеток. Так, например, процессор 0 (см. рис. 6.13), передав после обработки своего блока граничные данные и запустив, тем самым, вычисления на процессорах 1 и 4, оказывается готовым к исполнению следующей итерации метода Гаусса-Зейделя. После обработки блоков первой (процессорах 1 и 4) и второй (процессор 0) волн, к вычислениям окажутся готовыми следующие группы процессоров (для первой волны — процессоры 2, 5 и 8, для второй волны — процессоры 1 и 4). Кроме того, процессор 0 опять окажется готовым к запуску очередной волны обработки данных. После выполнения NB подобных шагов в обработке будет находиться одновременно NB итераций и все процессоры окажутся задействованными. Подобная схема организации расчетов позволяет рассматривать имеющуюся процессорную решетку как вычислительный конвейер поэтапного выполнения итераций метода сеток. Останов конвейера может осуществляться, как и ранее, по максимальной погрешности вычислений (проверку условия остановки следует начинать только при достижении полной загрузки конвейера после запуска NB итераций расчетов). Необходимо отметить также, что получаемое после выполнения условия остановки решение задачи Дирихле будет содержать значения узлов сетки от разных итераций метода и не будет, тем самым, совпадать с решением, получаемого при помощи исходного последовательного алгоритма.

Рис. 6.13. Организация волны вычислений при блочной схеме разделения данных

Оценка трудоемкости операций передачи данных

Время выполнения коммуникационных операций значительно превышает длительность вычислительных команд. Оценка трудоемкости операций приема-передачи может быть осуществлена с использованием двух основных характеристик сети передачи: латентности (latency), определяющей время подготовки данных к передаче по сети, и пропускной способности сети (bandwidth), задающей объем передаваемых по сети за 1 сек. данных – более полное изложение вопроса содержится в разделе 3 пособия.

Пропускная способность наиболее распространенной на данный момент сети Fast Ethernet – 100 Mбит/с, для более современной сети Gigabit Ethernet – 1000 Мбит/с. В то же время, скорость передачи данных в системах с общей памятью обычно составляет сотни и тысячи миллионов байт в секунду. Тем самым, использование систем с распределенной памятью приводит к снижению скорости передачи данных не менее чем в 100 раз.

Еще хуже дело обстоит с латентностью. Для сети Fast Ethernet эта характеристика имеет значений порядка 150 мкс, для сети Gigabit Ethernet – около 100 мкс. Для современных компьютеров с тактовой частотой свыше 2 ГГц/с различие в производительности достигает не менее, чем 10000-100000 раз. При указанных характеристиках вычислительной системы для достижения 90% эффективности в рассматриваемом примере решения задачи Дирихле (т.е. чтобы в ходе расчетов обработка данных занимала не менее 90% времени от общей длительности вычислений и только 10% времени тратилось бы на операции передачи данных) размер блоков вычислительной сетки должен быть не менее N=7500 узлов по вертикали и горизонтали (объем вычислений в блоке составляет 5N 2 операций с плавающей запятой).

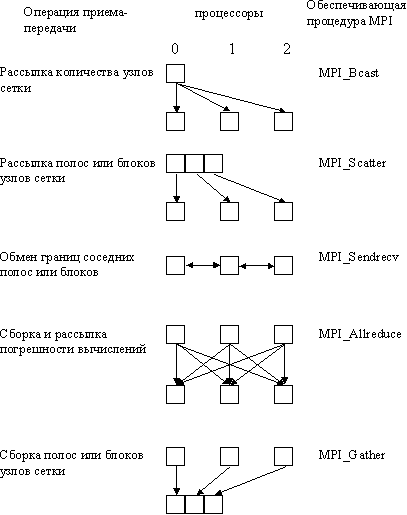
Как результат, можно заключить, что эффективность параллельных вычислений при использовании распределенной памяти определяется в основном интенсивностью и видом выполняемых коммуникационных операций при взаимодействии процессоров. Необходимый при этом анализ параллельных методов и программ может быть выполнен значительно быстрее за счет выделения типовых операций передачи данных – см. раздел 3 пособия. Так, например, в рассматриваемой учебной задаче решения задачи Дирихле практически все пересылки значений сводятся к стандартным коммуникационным действиям, имеющим адекватную поддержку в стандарте MPI (см. рис. 6.14):

— рассылка количества узлов сетки всем процессорам – типовая операция передачи данных от одного процессора всем процессорам сети (функция MPI_Bcast);

— рассылка полос или блоков узлов сетки всем процессорам – типовая операция передачи разных данных от одного процессора всем процессорам сети (функция MPI_Scatter);

— обмен граничных строк или столбцов сетки между соседними процессорами – типовая операция передачи данных между соседними процессорами сети (функция MPI_Sendrecv);

Рис. 6.14. Операции передачи данных при выполнении метода сеток в системе с распределенной памятью

— сборка и рассылка погрешности вычислений всем процессорам – типовая операция передачи данных от всех процессоров всем процессорам сети (функция MPI_Allreduce);

— сборка на одном процессоре решения задачи (всех полос или блоков сетки) – типовая операция передачи данных от всех процессоров сети одному процессору (функция MPI_Gather).

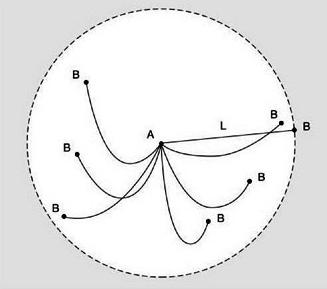
Принцип Дирихле: задачи с решениями

В математике существует множество принципов. Некоторые из них достаточно просты и понятны даже новичку, а некоторые требуют определенных объяснений и доказательств. Однако все они весьма эффективны, и их легко можно применять на практике. Одним из них является принцип Дирихле (известный также как принцип голубей/кроликов). Это достаточно простое утверждение, способное помочь в решении многих математических задач.

История

Данный принцип был сформулирован почетным немецким математиком Иоганном Дирихле еще в 1834 году. Сегодня его применяют в комбинаторике, а также в математической физике. В переводе с оригинального немецкого он звучит как «принцип ящиков». Свои исследования ученый проводил с кроликами и контейнерами. Он продемонстрировал, что если поместить, допустим, 5 кроликов в 7 контейнеров, то, по крайней мере, в одном контейнере будет находиться 5/7 от одного животного. Однако кролика нельзя разделить на части, следовательно, хотя бы одна клетка будет пустовать (5/7 равно 0 целых). Точно так же и в обратную сторону, если кроликов 7, а ящиков 5, то хотя бы в одном из них — 2 кролика (7/5 равно 2 целых). Отталкиваясь от этого утверждения, математику удалось сформулировать принцип, который обеспечивает успешное решение задач по математике уже многие годы.

Современная формулировка и доказательство

На сегодняшний день существует несколько разных формулировок данного принципа. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше чем k*k-1/k = k-1, а это противоречит первоначальным условиям.

В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.).

Еще одна формулировка

Иногда задачи на принцип Дирихле — не такие простые и очевидные, как с животными в ящиках. Необходимо переносить этот принцип на математические множества, чтобы отыскать какие-либо решения. В таком случае можно опираться на другую, более сложную формулировку.

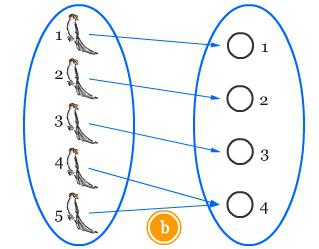
Если отобразить множество S, содержащее d+1 элементов, в множество R с совокупностью d элементов, то два элемента из множества S будут иметь одинаковый образ.

Хотя современные ФГОС по математике предъявляют к ученикам творческие требования и предлагают нестандартные варианты, решение через утверждение Дирихле не всегда такое простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.

Пример № 1. Геометрия

Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.

Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны.

Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Ну а сейчас — самое время применить принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.

Альтернативное решение

В данной задаче мы предположили, что в одной плоскости находятся точки А и В, однако принцип Дирихле не указывает конкретную ячейку, поэтому точно так же мы могли указать, что в одной плоскости разместились вершины С и В, или А и С. Для данной задачи совсем не важно, какую сторону треугольника не пересекает прямая k. Поэтому указанный принцип идеально подходит для ее решения.

Пример № 2. Геометрия

В середине равностороннего треугольника АВС (у которого АВ = ВС = АС = 1) разместилось 5 точек. Необходимо доказать, что две из них располагаются на расстоянии меньше 0,5.

Если провести в правильном треугольнике АВС средние линии, они разделят его на 4 маленьких правильных треугольника со сторонами ½ = 0,5. Предположим, что эти треугольники – ячейки, а точки внутри них – кролики. Получается, у нас есть 5 кроликов и 4 ячейки, следовательно, в одной из них будет находиться как минимум два кролика. Учитывая то, что точки не являются вершинами (так как они располагаются внутри треугольника АВС, а не на одной из его сторон), они будут размещаться внутри маленьких фигур. Следовательно, расстояние между ними будет меньше, чем 0,5 (поскольку величина отрезка внутри треугольника никогда не превышает величины его самой большой стороны).

Пример № 3. Комбинаторика

В других областях также можно удачно применять принцип Дирихле: комбинаторика и математическая физика уже давно опираются на него при решении задач.

Допустим, вокруг округлённого стола стоят на равном расстоянии друг от друга m флажков разных стран, а за столом сидят m представителей от каждой страны, причем каждый из них расположился рядом с чужим флажком. Нужно доказать, что при определенном вращении стола хотя бы двое из представителей окажутся возле своих флажков.

Получается, что существует m-1 способов развернуть стол так, чтобы изменилось взаиморасположение представителей и флажков (если исключить начальное размещение стола), но при этом остается m представителей.

Применим к решению утверждение Дирихле и обозначим, что представители выступают кроликами, а определенные положения стола при вращении – ячейками. При этом нужно провести аналогию между расположением представителя рядом с соответствующем флажком и заполненными ячейками. То есть положительный результат (1 представитель размешается возле своего флажка) равносилен результату «кролик оказывается в клетке». Мы понимаем, что у нас на одну ячейку меньше, чем нужно (m-1), а значит, в одной из них окажется как минимум 2 кролика. При этом не исключены ситуации, что какая-то клетка будет пустой (ни один представитель не совпал с флажком), а в какой-то клетке окажется два, три или даже больше кроликов (два, три и больше представителей совпадут с флажками). Таким образом, при одном определенном вращении как минимум два представителя очутятся возле своих флажков (как минимум два кролика попадут в одну ячейку).

Приступая к решению такой задачи, важно понимать, что начальное положение – это тоже ячейка, но по условию задачи она заведомо пустует, поэтому мы уменьшаем общее количество на 1 (m-1).

Пример № 4. Теория чисел

Принцип Дирихле в теории чисел также имеет огромное значение.

Предположим, на листике тетради в клетку ученик произвольно в узлах клеточек проставил 5 точек. Необходимо доказать, что как минимум один отрезок с вершинами в этих точках пройдет через узел клеточки.

Для начала нужно изобразить на листе тетради систему координат, основа которой расположится в одном из узлов. Оси системы координат будут совпадать с линиями сетки, а за единичный отрезок принята сторона клеточки. Получается, что все 5 отмеченных точек будут находиться в системе, а их координаты будут только целым числом (четным или нечетным). Таким образом, мы получим 4 варианта координат: (четный; четный), (нечетный; четный), (четный; нечетный) и (нечетный; нечетный). А значит, 2 из 5 точек будут соответствовать одному варианту. Если посмотреть на ситуацию с позиции Дирихле, то необходимо обозначить точки как зайцев, а варианты координат — как ячейки. Мы получаем 5 зайцев и 4 клетки, соответственно, в одной из них будет минимум 2 животных. Допустим, это точки Р и А, с координатами (x₄, y₃) и (x₅, y₆). Середина отрезка, соединяющего эти две вершины, будет иметь координаты ((x₄+x₅) / 2), ((y₃+y₆) / 2)), которые будут целыми числами в условиях соответствующей четности x₄ и x_5, y₃ и y₆. Получается, что середина отрезка расположилась в узле клетки.

Пример № 5

Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.

На прямой дороге вырыты маленькие поперечные канавки. Расстояние между всеми канавками одинаковое и равно оно Ö2 м. Необходимо доказать, что, независимо от ширины канавок, человек, шагающий по дороге с интервалом 1 м, однажды попадет ногой в одну из них.

Для того чтобы облегчить решение, необходимо вообразить, что дорогу можно «намотать» на окружность длиной в Ö2 метров. Получается, что все канавки сольются в 2 противоположных, а шаги человека будут отображаться в форме дуги, равной 1 м. Нам необходимо последовательно отметить все шаги, пока один из них не окажется в дуге, обозначающей канавку, независимо от того, какая будет длина k дуги (ширина канавки). Конечно, очевидно, что если бы человек шагал на расстояние, равное меньше, чем k, то он рано или поздно наступил бы в канаву. Ведь у человека никак не получится переступить расстояние k, если длина его шага меньше, чем k. А значит, нам необходимо найти два следа, расстояние между которыми не будет превышать величину k. Для этого уместно будет воспользоваться принципом Дирихле. Мы мысленно разделим всю окружность на дуги размером меньше k и будем считать их ячейками. Допустим, их окажется n штук. Предположим, что число шагов будет больше чем число дуг (n + m), хотя никакие два шага не будут совпадать из-за иррациональности числа Ö2, тогда по принципу Дирихле, по крайней мере, в одной из ячеек разместится больше одного шага. А поскольку длина дуги составляет меньше k, то и расстояние между шагами будет меньше. Таким образом, мы обнаружили необходимые для доказательства шаги.

Обобщение принципа

Материалы по математике, кроме стандартных (простых и не очень) формулировок, содержат также одну обобщенную, которая используется для выявления более двух объектов, похожих друг на друга. Она утверждает, что если dm + 1 кроликов поместить в d ячеек, то как минимум m + 1 кролик окажется в одной ячейке.

Пример № 6. Обобщение

Прямоугольник с площадью 5 х 6 клеток (30 клеток), закрашенных только 19. Можно ли обнаружить квадрат площадью 2 х 2 клетки, в котором минимум три будут закрашены?

Нашу фигуру необходимо разделить на 6 блоков по 5 клеток. Исходя из утверждения Дирихле, в одной из них будет закрашено не менее 4 клеточек (19/6 = 4). Тогда в одном из квадратов площадью 4 клеточки, расположенном в одном из блоков, будет закрашено минимум 3 клетки.

Пример № 7

Класс, в котором 25 человек. Из любых случайно выбранных 3 учеников двое будут друзьями. Необходимо доказать, что в классе находится школьник, у которого больше 11 приятелей.

Два решения вопроса

Для начала возьмем двух школьников, которые не дружат с друг другом (поскольку если бы все они дружили между собой, то в каждой тройке было бы три друга и каждый ученик дружил бы с 24 другими). Оставшиеся 23 одноклассника будут дружить с одним из нашей двойки, поскольку в противном случае нашлась бы тройка, где нет друзей (а это противоречит изначальному условию задачи). Получается, что один из двух школьников будет дружить как минимум с 12 учениками. В данном случае ученики – это кролики, а условия «друзья они или нет» – это ячейки. Мы имеем 23 животных и только 2 клетки. Соответственно, в одной из них как минимум 23/2 = 11,5, т. е. 12 кроликов. То есть один из 2 выбранных нами учеников будет дружить как минимум с 12 своими одноклассниками (или даже больше). Конечно же, существуют и другие методы решения задачи, однако данный — один из самых понятных и удобных.

Численные методы решения уравнений эллиптического типа

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

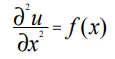
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

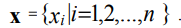
Граничные условия первого рода (условия Дирихле) для рассматриваемой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматриваемой задачи могут быть представлены в виде:

(5)

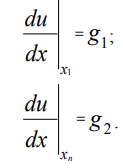
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, получим:

(6)

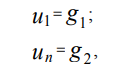
где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), получим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, получим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

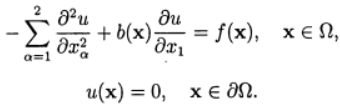
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

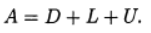
Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

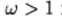
На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

Рындин Е.А. Методы решения задач математической физики. – Таганрог:
Изд-во ТРТУ, 2003. – 120 с.
Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
«ЛИБРОКОМ», 2010. — 320 с.

источники:

http://www.syl.ru/article/174987/new_printsip-dirihle-zadachi-s-resheniyami

http://habr.com/ru/post/418981/