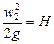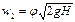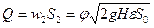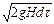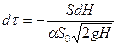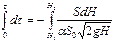Примеры технического приложения уравнения д бернулли

Некоторые приложения уравнения Бернулли

Особенности расположения молекул в жидкости

Жидкость — одно из трёх агрегатных состояний вещества (не считая 4-го состояния, называемого «плазма» – вещество, частицы которого ионизированы). Все агрегатные состояния различаются организацией молекул. В отличие от твёрдого (кристаллического) состояния, характерного строго упорядоченным расположением частиц вещества (кристаллическая решётка), в жидкости нет дальнего (распространяющегося на весь кристалл) порядка расположения атомов (молекул). Для организации молекул жидкости характерен недолговечный «ближний порядок», при котором молекулы группируются небольшими «коллективами», причём время жизни молекулы в данном «коллективе» очень непродолжительно (

10 -11 с). Затем происходит переход из одного «коллектива» в другой.

Жидкое состояние является промежуточным между твёрдым и газообразным состоянием вещества. Расстояние между молекулами в газах во много раз превышает размеры молекул. В жидкости же молекулы размещены вплотную друг к другу, со средним расстоянием между их центрами d порядка размера молекулы (d »10¸100 Å; где Å – ангстрем, 1 Å =10 -10 м ). Поэтому, плотности жидкостей на несколько порядков больше плотностей газов, и почти не отличаются от плотностей твёрдых тел. Более того, плотность металлов при плавлении уменьшается в среднем на 3%.

Основные свойства жидкостей:

1)текучесть;объясняется преимущественными переходами молекул из одного «коллектива» в другой в направлении действия внешней силы (например, силы тяжести); если внешние силы скомпенсированы, то переходы молекул из одного положения равновесия («коллектива») в другое происходят с одинаковой частотой и жидкое тело сохраняет свою форму;

2) несжимаемость (по сравнению с газами); объясняется достаточно плотным расположением молекул в жидкости. Примеры: а) удар молотом по полому металлическому ядру, заполненному жидкостью Þ поверхность ядра покрывается «испариной»; б) «потение» цилиндров гидравлических машин; в) на глубине »1 км в море, где давление достигает 100 атмосфер, плотность воды увеличивается всего на 0,5%.

Идеальная жидкость

Идеальной называют абсолютно несжимаемую жидкость, молекулы которой не притягиваются друг к другу.

4.2.1. Уравнение неразрывности струи

Линии тока – линии, касательные к которым в каждой точке потока совпадают с направлением скорости частиц жидкости. Линии тока не пересекаются между собой (иначе получилось бы, что в точке их пересечения частица жидкости имеет два направления движения). Значит, жидкость не проникает сквозь поверхность, образованную линиями тока.

Трубка тока — объём жидкости, ограниченный линиями тока. Рассмотрим такую трубку тока идеальной жидкости, в произвольном поперечном сечении которой скорость частиц жидкости одинакова. Выберем два любых сечения такой трубки тока: , характеризуемое скоростью , и , характеризуемое . Так как идеальная жидкость несжимаема, а её поток неразрывен и не проходит через боковую поверхность трубки, то за время через оба сечения пройдут одинаковые объёмы V жидкости:

= , т.е. = . (*)

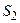
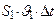
Выражение (*) называют уравнением неразрывности струи; оно хорошо применимо не только для каналов с вязкой жидкостью, но и с газом.

Вывод: при сужении канала скорость течения жидкости в нём увеличивается, при расширении — уменьшается.

4.2.2. Уравнение Бернулли (1738 г., Швейцария)

Выделим в ламинарном (не имеющем вихрей) потоке идеальной жидкости наклонную трубку тока, а в ней область, ограниченную сечениями S₁ и S₂. Определим изменение механической энергии , происходящее в этой области за . За это время в выделенную область втекает масса жидкости, ограниченная сечениями S₁ и вытекает — . Тогда:

.

В силу непроницаемости для жидкости стенок трубки тока, имеем = . Тогда можно записать:

DW= + — . (**)

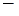
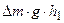
Но, согласно закону сохранения энергии, равно работе Авнешних сил (давления) и по перемещению массы жидкости внутри выделенного объёма: А = А₁ + А₂, где А₁ = ,А₂ = (знак ‘-‘ учитывает тот факт, что сила направлена навстречу потоку жидкости). Учитывая, что (где р — давление), получим :

— = , (***)

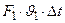
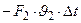
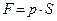
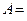
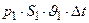
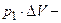
Приравняв (**) и (***), получим:

+ + = + + .

Разделив обе части последнего уравнения на и учтя, что (плотность), получим:

+ + = + + .

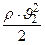
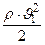
Так как сечения S₁иS₂ были выбраны произвольно, то:

+ + р = const

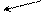
О физическом смысле слагаемых, входящих в уравнение Бернулли: — кинетическая энергия единицы объёма жидкости; — потенциальная энергия единицы объёма жидкости в гравитационном поле планеты; р — потенциальная энергия единицы объёма жидкости, обусловленная силами внешнего давления.

С другой стороны, так как единицы измерения всех слагаемых уравнения — Па(скаль), то эти слагаемые можно рассматривать и как давления: — динамическое (обусловленное движением жидкости), — весовое (обусловленное гравитационным притяжением жидкости к Земле), р– статическое, равное внешнему давлению, оказываемому на жидкость (например, давление поршня или атмосферы).

Вывод: в установившемся потоке жидкости сумма всех видов давления в любом поперечном сечении потока неизменна.

4.3.3. Частные случаи применения уравнения Бернулли

В этом случае уравнение Бернулли принимает вид:

= .

Так как модуль скорости зависит от площади поперечного сечения S, то величину Sможно выбрать столь малой, что динамическое давление значительно возрастёт, а статическое давление р станет меньше атмосферного р_о,и такая труба начнёт всасывать воздух, т.е. в сужениях (где скорость увеличивается) горизонтального канала статическое давление понижается. На этом принципе работают водоструйные насосы, ингаляторы, пульверизаторы.

2) Измерение скорости жидкости трубкой Пито.

Давления на входных отверстиях прямой и изогнутой трубок отличаются на величину динамического давления , которое уравновешивается дополнительным гидростатическим давлением более высокого столба жидкости . Из равенства = получим: = .

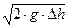
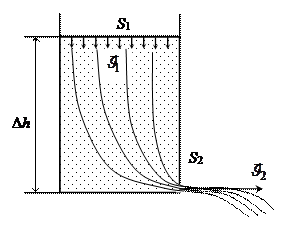
3) Истечение жидкости из отверстия. Формула Торричелли.

Так как >> , то, в силу уравнения неразрывности струи,

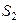
Примеры практического применения уравнения Д. Бернулли

Примеры практического применения уравнения Д. Бернулли

Примеры практического применения уравнения Д. Бернулли. Уравнение д. Бернулли является основным уравнением механики жидкости, вычисленным с его помощью Формула в случае движения жидкости разнообразна и решается множество практических задач. Для измерения скорости используется специальная гидродинамическая трубка 2, называемая трубкой Пито(рис. 4.20, а).Эта трубка размещена в точке измерения потока жидкости и имеет изогнутый конец к потоку и работает совместно с нормальным пьезометром 1. 71.

Трубка Пито 2 пропускает жидкость в отверстие, то есть под действием высокоскоростного давления вода в ней поднимается выше пьезометра 1.Нарисуйте сравнительную плоскость в центре отверстия в изогнутом конце трубки. Рисунок 4.20, а также горизонтальный след плоскости сравнения ОГ-ОГ. Выберите 2 раздела.1-1-перед входом в трубу, и 2-2-на поверхности воды в трубе, D. Я собираюсь написать уравнение Бернулли. Г1. П. С. \ 98. + С128 С±+ 2PR8.

Перепад давления в сужающих устройствах в производственных условиях измеряется обычно дифференциальными ртутными манометрами, а в лабораторных — пьезометрами. Людмила Фирмаль

• Затем-Прандтль сделан из малого диаметра и обтекаемого носа, но даже в этом случае будет наблюдаться турбулентность flow. So, обычно значение скорости, полученное по формуле (4.76), умножается на экспериментально определенный калибровочный коэффициент cp. Заводская труба f = 1… 1.04. Расход воды в трубопроводе обычно определяется с помощью пьезометра или расходомера Вентури (рис. 4.21).Измеритель прокачки Venturi ввод в главную трубу малого диаметра трубы O с ровным входом и outlet.

В узкой части, по сравнению с основной трубой, скорость увеличивается, а давление уменьшается. Сравнительная плоскость Og-Oy выбирается вдоль оси трубы, а участки 1-1 и 2-2 выбираются в предварительно суженной и суженной части. D в этих разделах. Уравнение Бернулли может быть выражено как: Г1 + D. потому что вода не движется через Пито tube. It нет необходимости рассматривать потери энергии уравнения Бернулли. Эта формула описывается в виде основной струйки.

• Это связано с тем, что локальная скорость в точке, где установлена эта формула, измеряется tube. In в этом случае r±-0,0! = И » 2 = 0 (поскольку вода не движется в трубке), измерьте давление на поверхности жидкости в трубке N Rl I » 2 /! = 0, то= r. Как видно из рисунка, r2 =и、 Где k-разность показаний водяного знака в трубке. Следовательно、 И= ущ. (4.76)） Для удобства использования трубка Пито и пьезометр конструктивно встроены в корпус 1 (рис. 4.20, б). Такая трубка называется трубкой пирога РГ. 98. 2 8. 4+ Р а. 98. 4. 28. + ВСН 1-2.

Игнорируйте потери энергии H ^ 1_2, потому что расстояние между секциями невелико, а сужение гладкое. Для горизонтальных труб (rx = r2) используйте коэффициент a = 1. П \ я Г Р2 Р = Р8 + 4 P8 1 2 8 2 8 P \ P * _ 1 C ^ ММ|) 4 П8, П8, 28, 2, 8. Используя уравнение неразрывности (4.30), K, Людмила Фирмаль

• Фактическое потребление будет несколько меньше теоретического значения (4.77) из-за потерь энергии и может быть выражено в виде зависимости. Р-калибровочный коэффициент, и его значение обычно составляет Р = 0,95… 0.97. D. Используя уравнение Бернулли, расход насоса(?Максимальная высота оси центробежного насоса над уровнем воды в скважине at / g » ac (рис. 4.22) может быть определена Значение очень мало、 Х. Поскольку скорость движения воды в скважине U0 (опускание на поверхность) пренебрежимо мала, ее можно игнорировать без потери точности расчетов. И Ug =V.

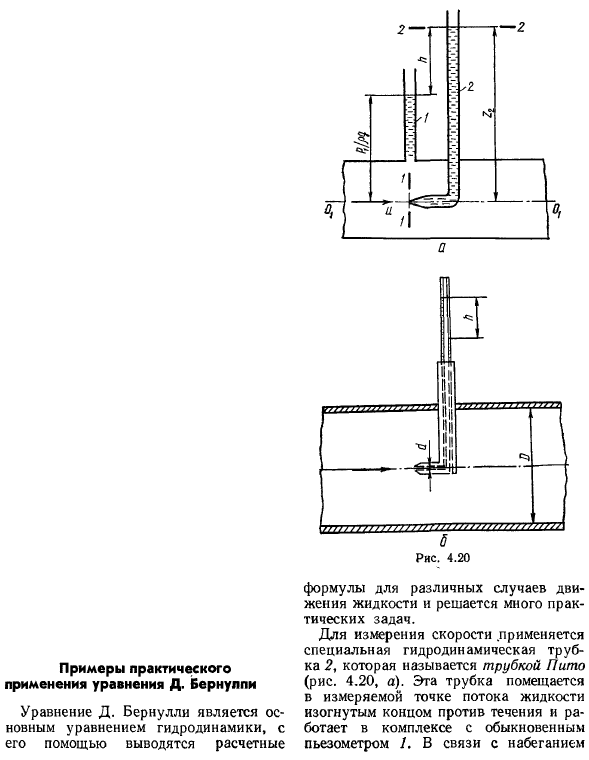
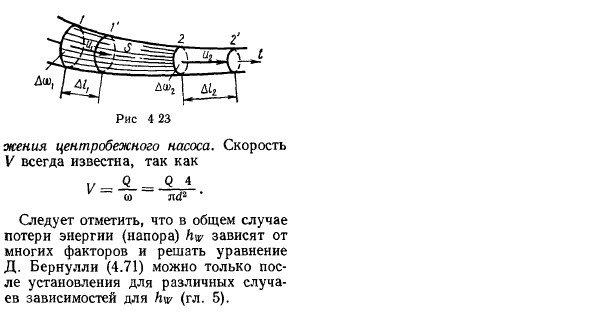
Напишите уравнение Бернулли и отнесите о-к плоскости отсчета Ришор. Секция I вакуумная-1, то есть известная quantity. So … ЛВ.= = ^^Л*. (4.79). Зависимость (4.79) базовая формула для определения высоты местоположения73. Центробежный насос. Скорость V всегда известна. В общем случае потери энергии (давления) k ^зависят от многих факторов, D. Отметим, что уравнение Бернулли(4.71) может быть решено только после установления зависимости km в различных случаях(Глава 5).

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Некоторые практические приложения уравнения Бернулли

Рассмотрим применение уравнения Бернулли для определения ско­ростей и расходов и времени истечения жидкостей из резервуаров.

Принципы измерения скорости и расхода жидкости. Для определения скоростей и расходов жидкостей в промышленной практике обычно при­меняются дроссельные приборы и пневмометрические трубки.

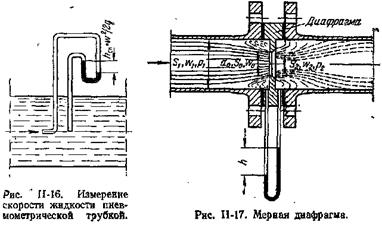
Принцип работы пневмометрических трубок, напри­мер трубки Пито-Прандтля, может быть пояснен с помощью рис. II-16. В каждом сечении разность уровней жидкости в трубках, изображенных на рисунке, выражает скоростной напор h_ск в точке сечения, лежащей на оси трубы.

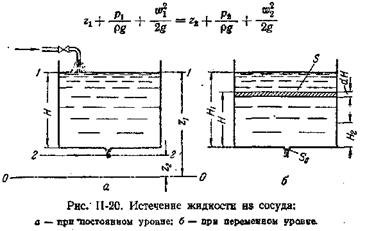
Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, как показано на рис. II-16, а при помощи дифференциального манометра (рис. II-17). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя (например, вода или спирт – при работе с газами или ртуть – при работе с капельными жидкостями). Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.

По результатам измерений 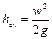находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода (рис. II-10), передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю ско­рость на площадь поперечного сечения трубопровода.

Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.

Более широко распространено определение скоростей и расходов жидкостей с помощью дроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. При искусственном сужении сечения потока посредством дроссельного прибора скорость и, соответственно, кинетическая энергия потока в этом более узком сечении возрастают, что приводит к уменьшению потенциальной энергии давления в том же сече­нии. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему — скорость и расход жидкости.

В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури.

Мерная диафрагма (рис. II-17) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло (рис. II-18) является насадкой, имеющим плавно закругленный вход и цилиндрический выход. Дифманометры мерных сопел (а также диафрагм) присоединяют к трубопроводу через кольцевые камеры а, соединенные с внутренним пространством трубопровода отверстиями, равномерно расположенными по окружности, или двумя каналами b.

Труба Вентури (рис. II-19) имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вслед­ствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть уста­новлены между фланцами трубопровода.

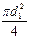
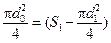
В трубе Вентури и в сопле площадь сечения сжатой струи S₂ = равна площади самого отверстия S₀ — — площадь сечения трубопровода, на котором установлен дроссельный прибор. В диа­фрагме S₂ S₂), а также потеря напора в диафрагме.

Коэффициент a называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:

(II,55)

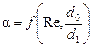
Значения a, определенные опытным путем, приводятся в специальной и справочной литературе.

Диаметр дроссельного устройства обычно в 3-4 раза меньше диаметра трубопровода, поэтому величиной (d₂/d₁) 2 в уравнении (II,54) можно в первом приближении пренебречь и находить расход жидкости по урав­нению

(II,56)

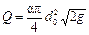
Среднюю скорость жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода. Опуская индексы «1» у w₁ и d₁, получим

(II,57)

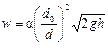
В случае работы со сжимаемыми жидкостями (газом или паром) при больших перепадах давлений в уравнения (II,56) и (II,57) вводят еще один поправочный коэффициент, учитывающий изменение плотности газа (пара).

Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уро­вень H жидкости (рис. II-20, а).

Вытекающая из такого отверстия струя резко сжимается при выходе вследствие инерционного движения частиц жидкости, приближающихся внутри сосуда к отверстию по криволинейным траекториям (некоторые из них даже непосредственно перед выходом еще скользят почти парал­лельно днищу, то есть перпендикулярно оси струи). Расстояние от днища до сжатого сечения (вслед за которым дальнейшее сужение струи из-за увеличения скорости падающей жидкости выражено гораздо слабее) невелико и составляет около половины диаметра отверстия.

Выбрав плоскость сравнения 0—0 параллельной днищу сосуда, напи­шем уравнение Бернулли (считая жидкость идеальной) для сечения 1—1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2—2, плоскость которого проходит через указанное сжатое сечение вытекающей струи:

Для открытого сосуда р₁ = р₂; кроме того, при постоянном уровне жидкости скорость ее w₁ = 0. Пренебрегая небольшим расстоянием от плоскости отверстия в днище сосуда до плоскости сжатого сечения струи, можно принять, что z_l — z₂ » H. Отсюда

(II,58)

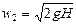
что соответствует известной формуле Торричелли.

При движении реальной жидкости часть напора H теряется на трение и преодоление сопротивления, обусловленного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости в сжатом сечении:

где j — поправочный коэффициент (j 3 /сек) жидкости равен произведению ее ско­рости w₂ на площадь сжатого сечения S₂ струи. Обозначим отношение S₂ площади поперечного сечения S₀ отверстия в днище через e. Это отно­шение e = S₂/S₀ называют коэффициентом сжатия струи.

(II,59)

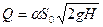
Коэффициент a представляет собой коэффициент расхода и выражается произведением коэффициентов скорости и сжатия струи:

Этот коэффициент определяют опытным путем, его значения зависят от значения критерия Re и могут быть найдены в справочниках в зависи­мости от свойств и скорости жидкости, а также от формы отверстия, его размера и удаленности от стенок сосуда.

Из уравнения (II,59) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидко­сти над отверстием и от размера отверстия, но не зависит от формы сосуда. Это уравнение применимо также для определения расхода жидко­сти, вытекающей через отверстие в тонкой боковой стенке сосуда, если считать Н расстоянием от верхнего уровня жидкости до оси отверстия.

Для жидкостей, по вязкости мало отличающихся от воды, можно при­нимать в первом приближении ее a » 0.62. При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнитель­ная потеря напора на входе и выходе жидкости, что приводит к сниже­нию j. Вместе с тем струя при входе в патрубок после некоторого сжатия снова расширяется и вытекает, заполняя все его сечение, т.е. можно счи­тать e = I. В итоге коэффициент расхода жидкости при истечении через насадок оказывается большим, чем при истечении через отверстие, и для воды может быть принят a » 0.82.

Если сосуд, из которого вытекает жидкость, закрыт и давление р₂ над жидкостью в нем отличается от наружного давления р₁, то при опре­делении расхода по формуле (II,59) вместо H в нее следует подставить 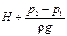, где r — плотность жидкости.

Теперь рассмотрим истечение при переменном уровне жидкости в сосуде с целью определения времени опорож­нения сосудов.

При таком истечении жидкости (рис. II-20,б) ее уровень H в сосуде снижается во времени и, согласно уравнению (II,58), уменьшается также скорость истечения w₀. Следовательно, процесс истечения носит неста­ционарный характер.

Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты H₁ до некоторой высоты H₂. За бесконечно малый промежуток времени dt., в соответствии с уравнением (II,59), через отверстие в днище вытечет объем жидкости

dV = Qdt = aS₀

где S₀ — площадь поперечного сечения отверстия в днище сосуда.

За тот же промежуток времени dt уровень жидкости в сосуде пони­зится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S сосуда убыль жидкости в нем составит

Знак минус в правой части указывает на уменьшение высоты жидкости в сосуде.

Приравнивая, согласно уравнению неразрывности потока, эти объемы, получим

aS₀ 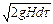= — SdH

Проинтегрируем это выражение, принимая, что коэффициент расхода a постоянен, т.е. не зависит от скорости истечения:

Таким образом, время опорожнения сосуда, имеющего постоянно поперечное сечение, от высоты H₁ до высоты H₂ составляет

(II,61)

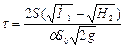
В случае полного опорожнения резервуара H₂ = 0 и уравнение (II,61) принимает вид

(II,61а)

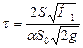
Решая задачу о времени опорожнения сосуда, площадь поперечного сечения которого изменяется по высоте (например, при истечении из конических резервуаров, горизонтальных цистерн и т.п.), следует при интегрировании выражения dt. учесть зависимость площади сечения S от уровня Н жидкости, т.е. учесть вид функции S = f(H).