Примеры уравнений с параметрами для 8 класса

Квадратные уравнения с параметром

Понятие уравнения с параметром и его решения

Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений.

Рассмотрим несложный пример.

Пусть нам дан прямоугольный участок площадью a. С точки зрения практической, мы хотим обнести участок забором, т.е. нас интересует зависимость периметра от длины x при некоторой площади a (ширина будет равна $\frac$):

Допустим, у нас есть материалы, чтобы соорудить забор длиной 100 м.

Это – простейшее уравнение с параметром, в котором один из коэффициентов не задан конкретным числом.

Уравнение относительно переменной x с параметром a – это уравнение F(x,a), в котором значение a не определено и также является переменной величиной.

Решить уравнение с параметром – это найти множество корней $$ для любого значения параметра a .

Решим наше уравнение. Найдём дискриминант:

$$ D = 50^2-4a = 2500-4a = 4(625-a) $$

Чтобы решения существовали, потребуем:

$$ D \ge 0 \Rightarrow 625-a \ge 0 \Rightarrow a \le 625 $$

При $a \lt 625$ два корня $x_ <1,2>= 25 \pm \sqrt<625-a>$

При a = 625 один корень $x_0 = 25$

При $a \gt 625$ решений нет

Наша модель немного усложнится, если мы поставим условия, чтобы площадь и длина были строго положительными:

Исследуем решение. Полученный корень $x_2 = 25+ \sqrt <625-a>\ge 25 \gt 0$ — положительный. И $x_1 = 25- \sqrt<625-a>$ при $0 \lt a \lt 625$ меняется в пределах $0 \lt x_1 \lt 25$, т.е. также положительный.

Запишем ответ для модели с условиями:

При $0 \lt a \lt 625$ два корня $x_ <1,2>= 25 \pm \sqrt<625-a>$

При a = 625 один корень $x_0$ = 25

При $a \gt 625$ решений нет

Ответ изменился незначительно, но чтобы его записать, нам пришлось провести дополнительное исследование.

Решить уравнение с параметром F(x,a) при дополнительных условиях на переменную x и параметр a – это найти допустимое множество корней $\$ для любого допустимого значения параметра a .

Заметим, что согласно полученным результатам, максимальная площадь, которую мы можем огородить нашим забором длиной 100 м, равна a = 625 $м^2$. Участок при этом представляет собой квадрат с длиной $x_0 = 25$ м и шириной $ \frac = 25$ м.

Примеры

Пример 1. При каких p квадрат разности корней уравнения $x^2-4x+p = 0$ равен 32?

Пусть $x_1, x_2$ — корни уравнения. По теореме Виета и условию задачи:

$$ <\left\< \begin x_1+x_2 = 4 \\ x_1 x_2 = p \\ x_1^2-x_2^2 = 32 \end \right.> \Rightarrow <\left\< \begin x_1+x_2 = 4 \\ x_1 x_2 = p \\ (x_1+x_2 )(x_1-x_2 ) = 32 \end \right.> \Rightarrow <\left\< \begin x_1+x_2 = 4 \\ x_1-x_2 = 8 \\ x_1 x_2 = p \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin 2x_1 = 4+8 = 12 \\ 2x_2 = 4-8 = -4 \\ x_1 x_2 = p \end \right.> \Rightarrow <\left\< \begin x_1 = 6 \\ x_2 = -2 \\ p = 6 \cdot (-2) = -12 \end \right.> $$

Пример 2. При каких значениях a уравнение

имеет один корень? Найдите этот корень.

$$ D = (a+2)^2-4(a+5) = a^2+4a+4-4a-20 = a^2-16 $$

Уравнение имеет один корень, если D = 0:

$$ a^2-16 = 0 \Rightarrow a = \pm 4 $$

При a = -4 уравнение имеет вид $x^2+2x+1 = 0$, т.е. $(x+1)^2 = 0$, $x_0 = -1$

При a = 4 уравнение имеет вид $x^2-6x+9 = 0$, т.е. $(x-3)^2 = 0, x_0 = 3$

При a = -4, $x_0$ = -1

При a = 4, $x_0$ = 3

Пример 3. Найдите такое p, чтобы уравнения

$$ x^2+x+p = 0 и x^2+px+1 = 0 $$

имели общий корень. Найдите этот корень.

Общий корень означает, что параболы пересекаются в точке, лежащей на оси OX.

$$ x(1-p) = 1-p \Rightarrow \left[ \begin <\left\< \begin p = 1 \\ x \in \Bbb R — любой \end \right.> \\ <\left\< \begin p \neq 1 \\ x = 1 \end \right.> \end \right. $$

При p = 1 уравнения совпадают $x^2+x+1 = 0$, но решений не имеют, т.к. $D \lt 0$.

При x = 1 уравнения парабол имеют вид: $p+2 = 0 \Rightarrow p = -2$.

При p = 2 уравнения имеют общий корень x = 1.

Пример 4. Найдите все целые значения a, при которых уравнение $\frac<4-a> = \frac<1>$ имеет решение.

Особая точка: a = 4. Уравнение $x^2-2x+4 = 0$ решений не имеет, т.к. $D \lt 0$.

Решаем уравнение в общем виде:

Потребуем $D \ge 0$

$$ -4(a-3)(a-1) \ge 0 \Rightarrow (a-3)(a-1) \le 0 $$

Начертим график параболы

Значение $f(a) \le 0$ не положительно, только на отрезке

Это значит, что $D \ge 0$, и уравнение имеет решения, только при трёх целочисленных a $\in$

При a = 1 и a = 3 D = 0, уравнение имеет вид $x^2-2x+1 = 0$ и одно решение $x_0 = 1$.

При a = 2 уравнение имеет вид: $x^2-2x = 0 \Rightarrow x(x-2) = 0 \Rightarrow \left[ \begin x_1 = 0 \\ x_2 = 2 \end \right. $

При a = 1 и a = 3 один корень $x_0 = 1$

При a = 2 два корня $x_1 = 0, x_2 = 2$

При всех других целых a уравнение решений не имеет.

Пример 5. При каких b и c уравнение $x^2+bx+c = 0$ имеет корнями b и c?

По условию $x_1 = b, x_2 = c$

По теореме Виета:

$$ <\left\< \begin x_1+x_2 = b+c = -b \\ x_1 x_2 = bc = c \end \right.> \Rightarrow <\left\< \begin c = -2b = -2 \\ b = 1\end \right.> $$

Уравнение $x^2+x-2 = 0$ имеет корнями 1 и -2.

Ответ: b = 1, c = -2

Пример 6. Найдите все значения параметра a, при которых уравнения

$$ x^2+(a^2+3a+7)x = 0 и x^2+(4a+19)x+(a^2+7a-44) = 0 $$

имеют один и те же решения.

Старшие коэффициенты парабол одинаковы и равны 1.

Параболы будут иметь одинаковые решения в том случае, если будут полностью совпадать, т.е.:

$$ <\left\< \begin a^2+3a+7 = 4a+19 \\ 0 = a^2+7a-44 \end \right.> \Rightarrow <\left\< \begin a^2-a-12 = 0 \\ a^2+7a-44 = 0 \end \right.> \Rightarrow <\left\< \begin (a-4)(a+3) = 0 \\ (a-4)(a+11) = 0 \end \right.> \Rightarrow a = 4 $$

Кроме того, они могли бы совпадать, если бы все переменные коэффициенты одновременно стали равны 0:

$$ <\left\< \begin a^2+3a+7 = 0 \\ 4a+19 = 0 \\ a^2+7a-44 = 0 \end \right.> \Rightarrow <\left\< \begin D \lt 0, a \in \varnothing \\ a = — \frac<19> <4>\\ a = \ <-11;4 \>\end \right.> \Rightarrow a \in \varnothing $$

Пример 7. Решите уравнение:

При a = 1 уравнение имеет вид $x^2 = 0$ и один корень $x_0 = 0$

Конспект «Решение квадратных уравнений с параметрами» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема урока: решение квадратных уравнений с параметрами.

Тип урока: комбинированный.

Планируемые результаты обучения:

личностные: логичность мышления, умение работать в проблемной ситуации;

предметные: формировать умение решать квадратные уравнения с параметром;

метапредметные: формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.

1. Организационный момент.

Приветствует учащихся, организует рабочее место,

Учащиеся настраиваются на работу.

2. Актуали-зация теоретических знаний.

Проводится опрос по теории

— Какое уравнение называется квадратным?

— Квадратным или линейным является уравнение

а) при b=6; б)0; в) b=0,5;

-Какое квадратное уравнение называется приведенным?

-Какое выражение называют дискриминантом?

-Сколько корней может иметь квадратное уравнение? (формулы).

-Теорема Виета и обратное утверждение.(записать)

Учащиеся предлагают различные варианты решения, говорят о трудностях, которые у них возникли.

Формировать личную мотивацию к учению.

Структурировать знания по данной теме

Учебное сотрудничество с учителем

3. Объяснение нового материа-ла.

При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при обращается в 0. Дело в том, что если этот коэффициент равен 0, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от D .

Учащиеся формулируют цель урока: «Научиться решать уравнения с параметром».

Взаимоконтроль и самоконтроль

Умение структурировать знания

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

4. Приме-нение знаний и умений в новой ситуации

Решение: Здесь коэффициент перед отличен от , значит, данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:

D =

D , значит, квадратное уравнение имеет два различных корня.

p +2 и p -1

Ответ: при любых значениях р p +2 ; p -1.

Пример 2. Решить уравнение p .

Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольное значение р=0, имеем два случая.

Если р=0, то получается уравнение вида 0+ х=1.

Если р≠0. То уравнение является квадратным, можно применять формулу D =—

4р(-1)=1-2р++4р=; ; .

Ответ: при р=0 х=1, при р≠0 ; .

Найдем значения параметра, обращающие в нуль коэффициент при х

Решим уравнение при а=1

0  х 2 +2(2  1+1)х+4  1+3=0  6х+7=0  .

Найдем значения параметра, обращающие в нуль дискриминант уравнения

4(5а+4)=0  .

Решим уравнение при , в этом случае уравнение будет иметь один действительный корень

 

9х 2 +6х+1=0  (3х+1) 2 =0  .

Решим уравнение при а  1, . В этом случае D  1, . В этом случае уравнение имеет два действительных корня

Ответ: 1) при , ;

2) при а=1, ;

3) при , действительных корней нет;

4) при и а  1, .

Пример 4. При каких значениях m ровно один из корней уравнения

Решение: Если нуль является корнем уравнения, значит квадратный трехчлен =0 обращается в нуль. =-3, =3.

Найдем второй корень при найденных значениях m .

Если m =3, то получаем =0, =-6.

Если m =-3, то получаем =0, которое имеет два кратных корня равных 0.

5. Закрепле-ние матери-ала

Работа в группах.

( а + 1 ) х 2 – 2 ( а + 9 ) х + 9 = 0;

С последующей проверкой.

Работа в группах. Проблемный диалог. Задают и отвечают на вопросы.

Контроль, коррекция, оценка

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

6. Домаш-нее задание.

1.При каких значениях а уравнение (а+2) +2(а+2)х+2=0 имеет один корень?

2.Решить уравнение .

3. Решить уравнение

4. Решить уравнение ( 2— b -6) = 4( b +1) x -2.

Объясняет какие номера обязательные и какие можно взять по выбору.

Учащиеся записывают домашнее задание и определяют для себя уровни заданий.

7. Итог урока. (1мин)

Какие цели стояли на уроке?

Достиг ли каждый из вас цели урока?

Фиксирую проблемы для следующего урока.

Самостоятельно определяют насколько достигнуты цели урока.

Формировать адекватную самооценку.

Формировать умения планировать свою работу.

Формулировать собственное мнение и аргументировать его.

Формулировать познавательную цель.

Учащимся предлагается по желанию продолжить предложение:

На уроке я научился (научилась) …

На уроке мне понравилось …

На уроке мне пригодились знания….

Для меня было сложно…

С урока я ухожу с … настроением!

Учащиеся продолжают предложения.

Смыслообразование, формирование положительного отношения к процессу познания

Оценка- выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.

Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

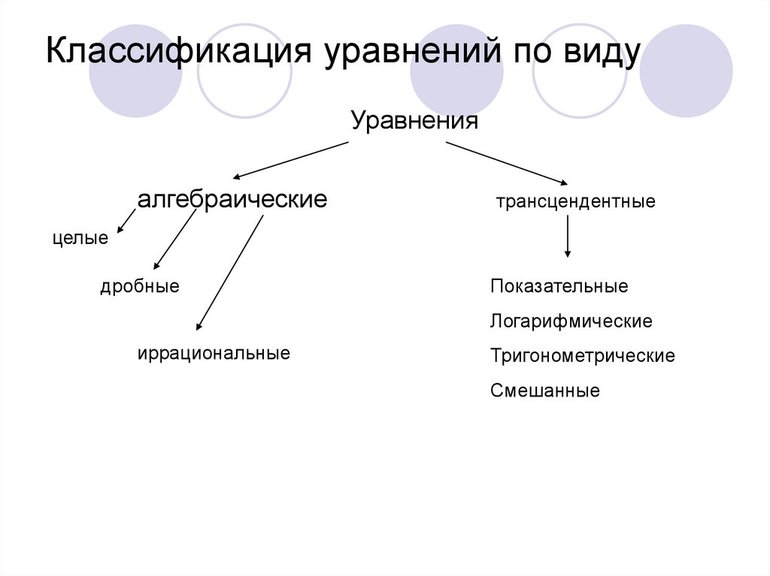
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

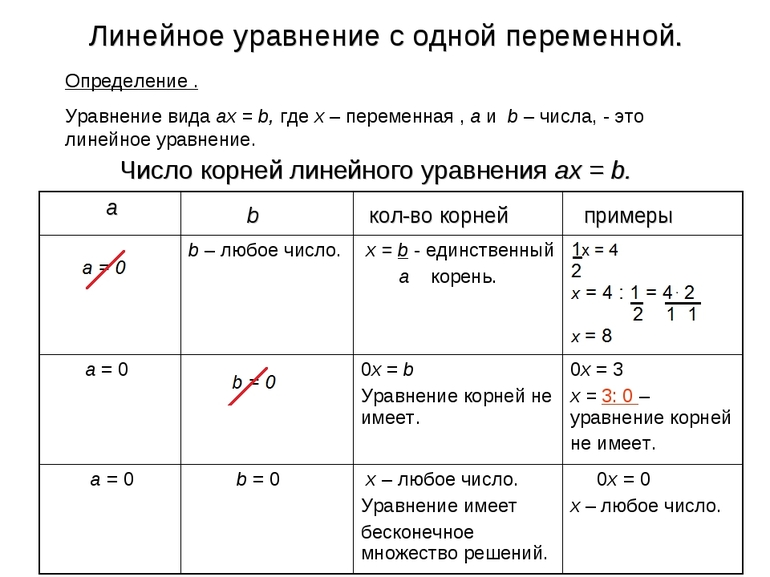
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.