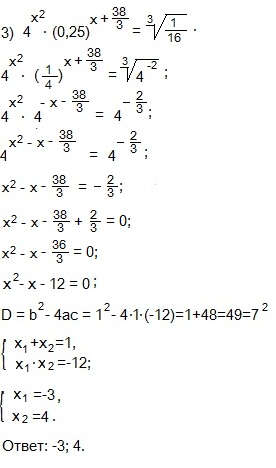Показательные уравнения, сводящиеся к квадратным
Разберем показательные уравнения, сводящиеся к квадратным. Их могут ученики кратко называть «квадратные показательные уравнения», хотя это название не точное. Однако, многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax 2 +bx+c=0.
Показательные уравнения, приводимые к квадратным на примерах
Уравнение 1
Решить уравнение:
1) 4 x +2 x+1 -3=0. Представим 4 x в виде степени с основанием 2.
(2 2 ) x +2 x ∙2 1 -3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:
вводим новую переменную: пусть 2 x =y;
y 2 + 2 y -3 =0.
Дискриминант для четного второго коэффициента: D1=1 2 -1∙(-3)=1+3=4=2 2 – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Возвращаемся к переменной х:
1) 2 x =-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).
2) 2 x = 1. Число 1 можно представлять в виде нулевой степени по любому основанию.
2 x = 2 0 ;
Уравнение 2
2) 0,25 2x -5∙0,5 2x +4=0. Решаем аналогично. Представляем 0,25 2x — в виде степени с основанием 0,5.
(0,5 2 ) 2x -5∙0,5 2x +4=0;
(0,5 2x ) 2 -5∙0,5 2x +4=0.
0,5 2x =y; ввели новую переменную у и получили приведенное квадратное уравнение:
y 2 — 5 y+ 4 =0;
Дискриминант D=b 2 -4ac=5 2 -4∙1∙4=25-16=9=3 2 — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
y1+y2= 5 , y1+y2= 4 . Корни приведенного квадратного уравнения находим подбором: y1=1, y2=4 и возвращаемся к переменной х:
1) 0,5 2x = 1 ; число 1 можно представлять в виде нулевой степени по любому основанию.
0,5 2x = 0,5 0 ;
2) 0,5 2 x =4; приведем степень 0,5 2 x к основанию 2, применив формулу: (1/a) x =а -х
2 -2 x =2 2 ; приравниваем показатели:
Уравнение 3

Представим левую и правую части в виде степеней с основанием 4, используя формулы: а -х =1/a x и a x ∙a y =a x + y .
Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.
Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Итак, решение показательных уравнений, которое мы разбирали в предыдущем уроке, пополнилось еще одним методом — приведением показательного уравнения к обычному квадратному уравнению. Такие уравнения называют — показательные уравнения, сводящиеся к квадратным.
Примеры уравнений, приводимых к квадратным. 9-й класс
Разделы: Математика
Класс: 9
Цели:
- сформировать умение решать целые уравнения методом введения новой переменной;
- развивать познавательную активность и творческие способности учащихся;
- воспитывать навыки творческого усвоения знаний.
Оборудование: компьютер, проектор .
1. Сообщение темы и цели урока
2. Проверка домашнего задания
– Какие уравнения называют целыми?
– Что называют степенью уравнения?
№ 273 (2 ст.), № 274 (а) – решение представлено на экране.
– Проверьте домашнее задание и поставьте себе оценку в табеле.
Табель оценок
Виды работ на уроке
Оценка
3. Устная работа
а) (х + 6) (х – 7) = 0 (Когда произведение равно 0?)
б) (10 – х) (4 – х) = 0
в) х(25 + х) (2 + х) = 0
г) х 2 = 25
д) х 2 – 9 = 27
4. Работа по объяснению нового материала. (Создание проблемной ситуации)
– Какова степень уравнения x 4 – 4х 2 + 5 = 0? (4)
– Умеем мы решать такие уравнения? (Нет) Давайте попробуем.
– Можно переписать уравнение в таком виде: (х 2 ) 2 – 4х 2 + 5 = 0?
– На какое уравнение похожа эта запись? (На квадратное)
– Почему я выделила х 2 ?
– Что я могу сделать с этим одночленом? (Заменить другой переменной)
– Пусть х 2 = у, тогда у 2 – 4у + 5 = 0
– Что мы получили при замене переменной? (Квадратное уравнение)
– Когда решим квадратное уравнение, значение какой переменной мы найдём? (у)
– Это будет ответ? (Нет)
– Что мы должны сделать дальше? (Вернуться к подстановке)
– Сколько у нас получится уравнений? (2)
– Чтобы найти значение х, мы должны решить оба эти уравнения.
– Сколько корней имеет уравнение?
– Отчего зависит количество корней уравнения? (От количества и знака корней уравнения с замененной переменной)
5. Презентация решений уравнений:
х 4 – 4х 2 + 5 = 0 и
(х 2 + х + 6)(х 2 + х – 4) = 144
6. Закрепление нового материала
У доски решение с комментированием и составлением алгоритма решения.
№276(а): (2х 2 + 3) – 12(2х 2 + 3) + 11 = 0
№278(а): х 4 – 5х 2 – 36 = 0
Алгоритм решения биквадратного уравнения
Метод решения – замены переменной
1. Ввести замену переменной: пусть х 2 = y,
2. Составить квадратное уравнение с новой переменной: аy 2 + by+ с = 0 (2)
3. Решить новое квадратное уравнение (2).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного уравнения.
7. Записать ответ.
7. Парная работа
Самостоятельное решение с взаимопроверкой. №276(б), 278(б)
8. Самостоятельная работа
в) г) д) е) одновременное решение у доски (на 4 досках). Проверка с помощью проектора.
7. Подведение итогов. Рефлексия
– Что нового узнали на уроке?
– Какие задания были сложными? Что запомнилось?
– Как работал класс на уроке?
– Кто работал лучше всех?
Поставить оценки за урок, используя табель оценок. (Табель сдается и проверяется учителем)
8. Домашнее задание: №279(обязательно), №280 (по выбору).
Квадратные уравнения
Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:
ax 2 + bx + c = 0 — квадратное уравнение,
где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
| x 2 + | b | x + | c | = 0. |
| a | a |
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x 2 + px + q = 0.
Уравнение x 2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
является приведённым, а уравнение:
можно заменить приведённым уравнением, разделив все его члены на -3:
Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax 2 + bx + c = 0 |  | ||||
| ax 2 + 2kx + c = 0 |  | ||||
| x 2 + px + q = 0 |
|
Обратите внимание на уравнение:
это преобразованное уравнение ax 2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Пример 1. Решить уравнение:
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Ответ: — | 1 | , -2. |
| 3 |
Определим, чему равны коэффициенты:
Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
Приведём уравнение к общему виду:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
http://urok.1sept.ru/articles/652480
http://izamorfix.ru/matematika/algebra/kvadratnye_uravn.html