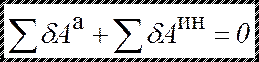Принцип даламбера лагранжа общее уравнение

iSopromat.ru

Принцип Даламбера-Лагранжа гласит: при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нулю.

В принципе возможных перемещений говорится о необходимых и достаточных условиях равновесия системы с идеальными связями, то есть если система находится в равновесии, то сумма работ внешних сил, приложенных к точкам системы, на их возможном перемещении равна нулю:

Принцип Даламбера позволяет говорить о равновесии сил, действующих на точки системы (но не о равновесии системы).

В эти силы входят: внешние силы, реакции связей, силы инерции, то есть

Объединяя эти два принципа (принцип Даламбера и принцип возможных перемещений), получаем для системы с идеальными связями уравнение

которое и выражает общее уравнение динамики (принцип Даламбера-Лагранжа).

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Принцип Даламбера-Лагранжа

Принцип Даламбера (п. 3.8) позволяет любую задачу динамики решать как задачу о равновесии. Если для решения задачи о динамическом равновесии применить принцип возможных перемещений (п. 3.9), получится новый метод решения задач динамики, который называется принципом Даламбера-Лагранжа.

Принцип Даламбера-Лагранжа. При движении механической системы с наложенными на нее идеальными связями сумма элементарных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю:

Это уравнение называется общим уравнением динамики или уравнением работ.

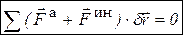
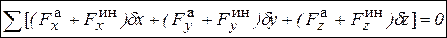
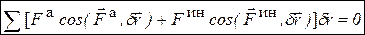
С учетом разных способов определения элементарной работы силы (табл. 3.3) общее уравнение динамики можно записать и использовать в разных формах: векторная , координатная , естественная .

В случае, когда среди связей, наложенных на механическую систему, есть неидеальные, при использовании общего уравнения динамики надо включить в него работу реакций неидеальных связей. Приняв общее уравнение динамики за исходное, можно вывести из него все основные теоремы динамики (п. 3.4, 3.5, 3.6).

Общее уравнение динамики позволяет также составить дифференциальные уравнения движения любой механической системы. Они составляются по каждому из независимых возможных перемещений (п. 3.9.1), поэтому количество уравнений движения равно числу степеней свободы механической системы. Но более рациональным подходом в этом случае является использование уравнений Лагранжа второго рода (п. 3.11) — дифференциальных уравнений движения механической системы в обобщенных силах.

Дата добавления: 2014-12-01 ; просмотров: 1441 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Общее уравнение динамики. Пример решения задачи

Условие задачи

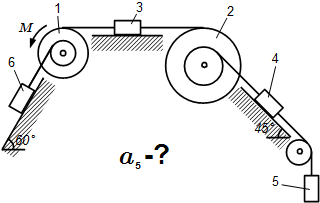
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R ₁ = 0,2 м , r ₁ = 0,1 м , а шкива 2 – R ₂ = 0,3 м , r ₂ = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ ₁ = 0,1 м и ρ ₂ = 0,2 м .

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Решение задачи

Дано: R ₁ = 0,2 м , r ₁ = 0,1 м , R ₂ = 0,3 м , r ₂ = 0,15 м , ρ ₁ = 0,1 м , ρ ₂ = 0,2 м . P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н , M = 10 Н·м .

Установление кинематических соотношений

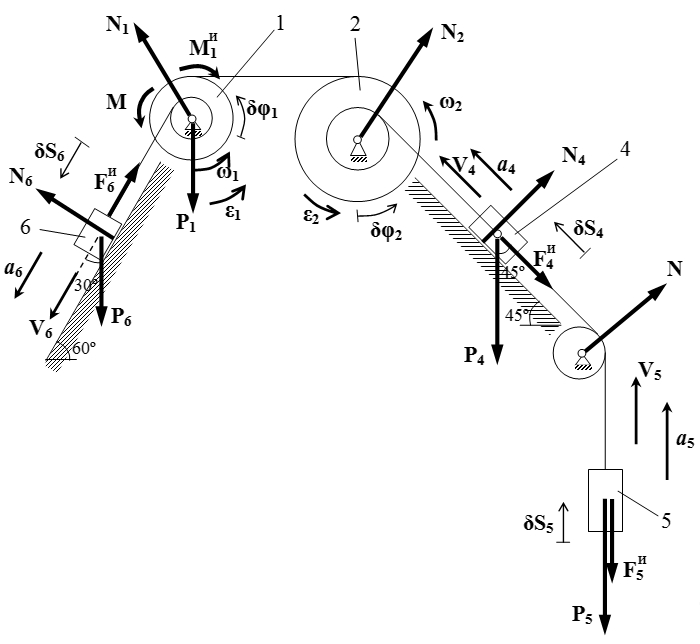
Установим кинематические соотношения. Пусть V ₄ , V ₅ , V ₆ , a ₄ , a ₅ , a ₆ , δS ₄ , δS ₅ , δS ₆ – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω ₁ , ω ₂ , ε ₁ , ε ₂ , δφ ₁ , δφ ₂ – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.

Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.

Итак, мы нашли связь между скоростями тел.
;
;
.

Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.

Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.

Активные внешние силы

Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P ₁ = 40 Н , P ₄ = 20 Н , P ₅ = 30 Н и P ₆ = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N ₁ , N ₂ и N шкивов 1, 2 и невесомого блока;
силы реакции N ₄ и N ₆ , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.

Силы инерции

Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.

Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε ₁ и ε ₂ , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a ₄ , a ₅ и a ₆ , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a ₅ . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).

Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a ₅ .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.

Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.

Применение общего уравнения динамики

Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS ₅ . Тогда угол поворота δφ ₁ шкива 1 и перемещения δS ₄ и δS ₆ грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.

Определение суммы работ внешних активных сил и сил инерции

Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.

Работа, произведенная моментом сил , вычисляется аналогично:
.

Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P ₁ , N ₁ , N ₂ и N не совершают работу. Поскольку силы N ₄ и N ₆ перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.

Находим сумму работ остальных активных сил и сил инерции.

.
Подставляем выражения для сил инерции и применяем кинематические соотношения.

.
Сокращаем на δS ₅ и преобразовываем.

.
Подставляем численные значения.

;
;
м/с 2 .

Автор: Олег Одинцов . Опубликовано: 02-08-2015