Принцип даламбера основные уравнения кинетостатики

Техническая механика

Основы кинетостатики

Метод кинетостатики в динамике.
Принцип Даламбера

Как известно, первый закон Ньютона гласит, что любое тело, любая материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения, пока какая-нибудь сила не нарушит это состояние. Этот закон называют законом инерции, а свойство материальных тел «неохотно» изменять свое текущее состояние покоя – инертностью.

Явление инертности использовал в идее оригинального принципа динамических расчетов французский ученый Ж. Д’Аламбер (д’Аламбер, Даламбер; фр. Jean Le Rond D’Alembert, d’Alembert, 1717-1783) , по имени которого этот принцип и назван.
Принцип Д’Аламбера (Даламбера) широко применяется для решения задач динамики методами кинетостатики.

Справедливости ради, следует отметить, что несколько раньше Д’Аламбера возможность решения задач динамики с помощью приемов статики изучали такие видные российские ученые Петербургской Академии наук, как Я. Герман и Л. Эйлер, жившие примерно в одно время с Даламбером.

Итак, что же такое принцип Д’Аламбера и чем он может быть полезен при решении задач динамики?

Сначала вспомним статику, где все легко и просто – любое тело или материальная точка будет находится в равновесии, если действующие на него силовые факторы уравновешивают друг друга. Все очевидно, просто и понятно. Благодаря приемам статики можно определить неизвестные активные или реактивные силы, действующие на уравновешенное тело или точку, применив простые математические приемы и геометрические построения.
Нельзя ли эти приемы использовать для подвижных тел, причем не просто подвижных, а движущихся с ускорением? Оказывается можно, а иногда даже просто необходимо, как указал знаменитый француз, увековечивший свое имя в известном потомкам принципе.

Представим себе материальную точку массой m движущуюся с ускорением a под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F .
Воспользуемся вторым (основным) законом динамики для того, чтобы уравнение движения этой точки записать в форме уравнений равновесия:

Выражение, стоящее в скобках называют силой инерции , и обозначают F ин .
Итак:

Сила инерции есть вектор, равный произведению массы материальной точки на ее ускорение в данный момент времени, и направлен в сторону, противоположную ускорению .
На основании этого определения можно записать:

F + F ин = 0 или Σ(F, F ин ) = 0 .

Это равенство и является математическим выражением принципа Д’Аламбера, который формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющих всем условиям равновесия .
Т. е. Д’Аламбер предложил оригинальный способ применения методов статики к движущимся материальным точкам, использовав при этом в качестве основного инструмента понятие инертности и силы инерции.

Утверждение, что тело якобы находится в состоянии равновесия во время ускоренного движения, может вызвать недоумение. Как это может быть?
Здесь следует отметить, что сила инерции, введенная в научную терминологию Д’Аламбером, является понятием условным, т. е. фактически такой силы в природе не существует, в отличие от понятия инертности — свойства любых материальных тел и точек, проявляющееся в стремлении сохранять свое состояние. Но именно условное уравновешивание силой инерции движущихся с ускорением тел, позволило использовать при решении задач динамики приемы статики, породив раздел теоретической механики — кинетостатику.

Явление инертности (инерции) можно пояснить на таком простом примере. Если подвесить на нити груз, который она легко выдержит в статическом состоянии, а затем резко дернуть за конец нити, то она порвется именно благодаря инертности груза.
Другой пример: если тяжелое чугунное ядро попытаться сдвинуть с места, то потребуется приложить немалое усилие, чтобы оно покатилось. Когда же ядро, наконец, покатилось, для его остановки потребуется, опять же, немалое мускульное усилие.
В каждом из этих случаев наглядно проявляется свойство инертности материальных тел.

Пример решения задачи методом кинетостатики

Задача: в кабине лифта размещены пружинные весы, на которых установлен груз. Когда кабина неподвижна показание весов составляет 50 Н, а при движении лифта показание весов увеличилось до 51 Н.
Определить, с каким ускорением движется кабина лифта.

Решение.
Применим к телу принцип освобождаемости, отбросим пружинные весы и заменим их реакцией R , равной натяжению пружины. Для решения задачи применим метод кинетостатики, т. е. приложим к телу силу инерции F ин .
Составим уравнение равновесия взвешиваемого тела, спроецировав все силы на вертикальную ось y ; предполагаем, что ускорение а кабины направлено вверх, и, следовательно, сила инерции направлена вниз (т. е. в противоположную ускорению сторону):

ΣY = 0 ; R – G – F ин = 0 .

Модуль силы инерции определяем по формуле:

Подставив это выражение в уравнение, определим ускорение:

a = (R – G)g/G = (51 – 50)×9,81/50 = 0,196 м/с 2 .

Ускорение получилось положительным, следовательно мы изначально правильно предположили, что оно направлено вверх (если бы получилось отрицательное значение, значит ускорение направлено вниз).

Силы инерции в криволинейном движении

В криволинейном движении точки полное ускорение равно векторной сумме касательного (тангенциального) и нормального (центростремительного) ускорений.

Касательное ускорение определяется по формуле a_τ = dv/dt , нормальное ускорение a_n = v 2 /ρ , полное ускорение a = √(a_τ 2 + a_n 2 ) .

Каждому ускорению соответствует своя сила инерции:

• Касательная (тангенциальная) сила инерции: F_τ ин = mdv/dt ;
• Нормальная (центробежная) сила инерции: F_n ин = mv 2 /ρ ;
• Полная сила инерции: F ин = ma .

В качестве примера рассмотрим равномерное движение по окружности, лежащей в горизонтальной плоскости, камня силой тяжести G , привязанного невесомой нитью длиной r , расположенной в той же плоскости (рис. 1) .
Чтобы нить оставалась в плоскости движения камня, предполагается, что он скользит по идеально гладкой горизонтальной плоскости.
Скорость движения камня обозначим v .

Тогда F_n ин = mv 2 /ρ — центробежная сила инерции (эта сила натягивает нить) ; R = mv 2 /ρ — центростремительная сила, приложенная к камню (эта сила удерживает камень на круговой траектории) .
Обе эти силы, согласно второму закону Ньютона, равны по модулю и направлены в противоположные стороны, т. е. уравновешивают друг друга.
Очевидно, что касательная сила в данном примере будет равна нулю, поскольку камень движется равномерно ( а_τ = 0 ).

Из опыта известно, что при достаточной скорости камня нить может не выдержать и разорваться, тогда камень полетит по касательной к окружности, т. е. по направлению имеющейся в момент разрыва нити скорости. Это доказывает, что центробежная сила инерции есть реальная сила для связи, но к телу она приложена условно.

Внутри тел, движущихся с ускорением, также возникают внутренние силы инерции, так как для каждой частицы тела соседние являются связями.

Найдем, чему будет равно натяжение нити, если камень движется по окружности, лежащей в вертикальной плоскости (рис. 2) . Для определения натяжения R нити применим принцип Д’Аламбера, т. е. приложим к камню нормальную силу инерции F_n ин и касательную силу инерции F_τ ин .

Спроецируем все силы в направлении нити, в результате чего получим:

R – G cosα – F_n ин = 0 , откуда: R = F_n ин + G cosα = mv 2 /r + G cosα .

Очевидно, что натяжение нити будет максимальное при α = 0, т. е. когда камень находится в нижнем положении:

Минимальное натяжение нити имеет место, когда α = π рад, т. е. в тот момент, когда камень находится в верхнем положении:

Следует отметить, что под влиянием силы тяжести в данном случае модуль скорости камня будет изменяться от максимума в нижнем положении до минимума в верхнем положении.

Если выразить линейную скорость камня через угловую скорость нити, используя зависимость v = ωr , то формула центробежной силы примет вид:

Пример решения задачи с использованием принципа Д’Аламбера

Задача: определить скорость v искусственного спутника Земли, движущегося по круговой орбите на высоте h = 230 км от поверхности Земли, радиус которой принять равным R = 6370 км.
Изменением ускорения свободного падения и сопротивлением атмосферы пренебречь.

Решение.
После того, как ракета-носитель вывела спутник массой m на орбиту и сообщила ему скорость v , направленную по касательной к орбите, спутник продолжает движение под действием одной лишь силы притяжения Земли.
Для определения скорости v спутника применим принцип Д’Аламбера, т. е. приложим к спутнику центробежную силу инерции и составим уравнение равновесия, спроецировав все силы на ось, проходящую через спутник и центр Земли:

Так как F_n ин = mv 2 /(R + h) , то можно записать: mg — mv 2 /(R + h) = 0 .

Сократив члены этого равенства на m (массу спутника) , получим:

Подставив значения, получим: v = √[9,81(6370 + 230)1000] ≈ 8000 м/с ≈ 8 км/с .

Принцип Даламбера теоретической механики

Вы будете перенаправлены на Автор24

Принцип Даламбера является в теоретической механике одним из главных принципов динамики. Согласно этому принципу, при условии присоединения силы инерции к активно действующим на точки механической системы силам и реакциям наложенных связей, получается уравновешенная система.

Данный принцип получил название в честь французского ученого Ж. Даламбера, впервые предложившего его формулировку в своем сочинении «Динамика».

Определение принципа Даламбера

Принцип Даламбера звучит следующим образом: если к воздействующей на тело активной силе прикладывается дополнительная сила инерции, тело будет пребывать в равновесном состоянии. При этом суммарное значение всех действующих в системе сил, дополненное вектором инерции, получит нулевое значение.

Согласно указанному принципу, в отношении каждой i-той точки системы, становится верным равенство:

• $F_i$ -активно воздействующая на эту точку сила,
• $N_i$ — реакция связи, наложенной на точку;
• $J_i$ — сила инерции, определяемая формулой $J_i=-m_ia_i$ (она направлена противоположно этому ускорению).

Фактически, отдельно для каждой рассматриваемой материальной точки $ma$ переносится справа налево (второй закон Ньютона):

$ma$ при этом называется силой инерции Даламбера.

Такое понятие, как сила инерции, было введено еще Ньютоном. Согласно рассуждениям ученого, при условии движения точки под воздействием силы $F=ma$, тело (или система) – становится источником этой силы. При этом, согласно закону о равенстве действия и противодействия, ускоряемая точка будет влиять на ускоряющее ее тело с силой $Ф=-ma$. Такой силе Ньютон дал название системы инерции точки.

Силы $F$ и $Ф$ будут равными и противоположными, но приложенными к разным телам, что исключает их сложение. Непосредственно на точку сила инерции воздействия не оказывает, поскольку для нее она представляет фиктивную силу. При этом точка оставалась бы в состоянии покоя, если бы, помимо силы $F$, на точку оказывала воздействие еще и сила $Ф$.

Готовые работы на аналогичную тему

Принцип Даламбера позволяет применять при решении задач динамики более упрощенные методы статики, что объясняет его широкое применение в инженерной практике. На этом принципе основывается метод кинетостатики. Особенно он удобен в применении с целью установления реакций связей в ситуации, когда известен закон происходящего движения или он получен при решении соответствующих уравнений.

Разновидностью принципа Даламбера выступает принцип Германа-Эйлера, фактически представлявшего собой форму данного принципа, но обнаруженную до появления публикации сочинения ученого в 1743 году. При этом принцип Эйлера не рассматривался его автором (в отличие от принципа Даламбера) в качестве основы для общего метода решения задач движения механических систем со связями. Принцип Даламбера считается более целесообразным в применении в случае необходимости определения неизвестных сил (для решения первой задачи динамики).

Принцип Даламбера для материальной точки

Многообразие типов решаемых в механике задач нуждается в разработке эффективных методик составления уравнений движения для механических систем. Одним из подобных методов, позволяющих посредством уравнений описать движение произвольных систем, считается в теоретической механике принцип Даламбера.

Опираясь на второй закон динамики, для несвободной материальной точки запишем формулу:

где $R$ представляет реакцию связи.

Эта формула является выражением принципа Даламбера для материальной точки, согласно которому, для движущейся в любой момент времени точки геометрическая сумма воздействующих на нее активных сил и силы инерции получает нулевое значение. Этот принцип позволяет записывать уравнения статики для движущейся точки.

Принцип Даламбера для механической системы

Для состоящей из $n$-точек механической системы, можно записать $n$-уравнений вида:

При суммировании всех этих уравнений и введении следующих обозначений:

которые являются главными векторами внешних сил, реакции связей и сил инерции соответственно, получаем:

Условием для равновесного состояния твердого тела является нулевое значение главных вектора и момента действующих сил. Учитывая это положение и теорему Вариньона о моменте равнодействующей в результате запишем такое соотношение:

примем следующие обозначения:

главные моменты внешних сил, реакции связей и сил инерции соответственно.

В итоге получаем:

Эти две формулы являются выражением принципа Даламбера для механической системы. В любой момент времени для движущейся механической системы геометрическая сумма главного вектора реакций связей, внешних сил, и сил инерции получает нулевое значение. Также нулевой будет и геометрическая сумма главных моментов от сил инерции, внешних сил и реакций связей.

Полученные формулы являются дифференциальными уравнениями второго порядка из-за присутствия в каждом из них ускорения в силах инерции (второй производной закона движения точки).

Принцип Даламбера позволяет решать методами статики задачи динамики. Для механической системы можно записывать уравнения движения в виде уравнений равновесия. Из таких уравнений можно определить неизвестные силы, в частности, реакции связей (первая задача динамики).

Силы инерции. Принцип Даламбера. Метод кинетостатики

Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО).

Основной закон динамики для неинерциальных систем отсчета: , где
— сила, действующая на тело со стороны других тел;

— сила инерции, действующая на тело относительно поступательно движущейся НСО. — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;

— центробежная сила инерции, действующая на тело относительно вращающейся НСО. — угловая скорость НСО относительно ИСО, — расстояние от тела до центра вращения;

— сила инерции, действующая на тело, движущееся со скоростью относительно вращающейся НСО. — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).

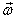
Принцип Даламбера.

Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.

Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой . Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение .

Введем в рассмотрение величину

,

имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки (иногда даламберовой силой инерции).

Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции , то полученная система сил будет уравновешенной, т.е. будет

.

Метод Кинетостатики.

Важнейшим из принципов механики является принцип Даламбера. С принципом Даламбера тесно связан метод кинетостатики — способ решения задач динамики, в котором динамические уравнения записываются в форме уравнений равновесия. Метод кинетостатики широко применяется в таких общеинженерных дисциплинах, как сопротивление материалов, теория механизмов и машин, в других областях прикладной механики. Принцип Даламбера результативно используется и внутри самой теоретической механики, где с его

помощью созданы эффективные способы решения задач динамики.