Принцип оптимальности уравнение беллмана реферат

Принцип оптимальности Беллмана

1.1 Принцип оптимальности Беллмана

Метод динамического программирования позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Процесс решения задачи разбивается на шаги. При этом нумерация шагов, как правило, осуществляется от конца к началу.

Основным принципом, на котором базируются оптимизация многошагового процесса, а также особенности вычислительного метода, динамического программирования, является принцип оптимальности Р. Беллмана.

Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующие решения должны быть оптимальными относительно состояния, полученного в результате первоначального решения.

Принцип оптимальности имеет конструктивный характер и непосредственно указывает процедуру нахождения оптимального решения. Математически он записывается выражением вида:

(1.3)

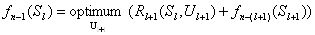
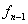
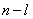
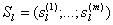
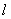
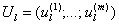
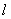
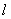
где — оптимальное значение эффекта, достигаемого за шагов; n — количество шагов (этапов); — состояние системы на — м шаге; — решение (управление), выбранное на — м шаге; — непосредственный эффект, достигаемый на — м шаге.

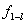
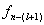
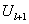
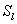
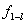
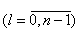
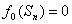
«Optimum» в выражении (1.3) означает максимум или минимум в зависимости от условия задачи. Все вычисления, дающие возможность найти оптимальное значение эффекта, достигаемого за n шагов, ¦n(So), проводятся по формуле (1.3), которая носит название основного функционального уравнения Беллмана или рекуррентного соотношения. Действительно, при вычислении очередного значения функции используются значение функции , полученное на предыдущем шаге, и непосредственное значение эффекта , достигаемого в результате выбора решения при заданном состоянии системы . Процесс вычисления значений функции осуществляется при естественном начальном условии , которое означает, что за пределами конечного состояния системы эффект равен нулю.[1, с 243]

1.2 Вычислительная схема

Оптимальное решение задачи методом динамического программирования находится на основе функционального уравнения (1.3). Чтобы определить его, необходимо:

1) Записать функциональное уравнение для последнего состояния процесса (ему соответствует ):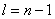

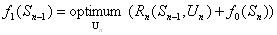
; (1.4)

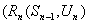
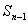
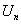
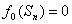
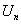
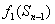
2) Найти из дискретного набора его значений при некоторых фиксированных и из соответствующих допустимых областей ( так как , то ). В результате после первого шага известно решение и соответствующее значение функции ;

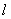
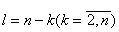
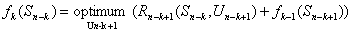
3) Уменьшить значение на единицу и записать соответствующее функциональное уравнение. При оно имеет вид:

; (1.5)

4) Найти условно-оптимальное решение на основе выражения (1.5);

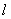
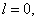
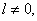
5) Проверить, чему равно значение . Если расчет условно-оптимальных решений закончен, при этом найдено оптимальное решение задачи для первого состояния процесса. Если перейти к выполнению п. 3;

6) Вычислить оптимальное решение задачи для каждого последующего шага процесса, двигаясь от конца расчетов к началу.[1, с 244]

2. Решение задачи оптимального распределения средств на расширение производства 2.1 Решение задачи оптимального распределения средств на расширение производства ручным способом

Широкий класс составляют задачи, в которых речь идет о наиболее целесообразном распределении во времени тех или иных ресурсов (денежных средств, рабочей силы, сырья и т.п.). Рассмотрим пример задачи такого рода.

Производственному объединению из четырех предприятий выделяется банковский кредит в сумме 60 млн. ден. ед. для реконструкции и модернизации производства с целью увеличения выпуска продукции. Значения 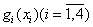дополнительного дохода, получаемого на предприятиях объединения в зависимости от выделенной суммы xi, приведены в табл. 2.1. Распределить выделенный кредит между предприятиями так, чтобы дополнительный доход объединения был максимальным.[1, с 261]

Таблица 2.1 – Значения дополнительного дохода

Применение метода динамического программирования в задачах принятия решений

Автор работы: Пользователь скрыл имя, 15 Октября 2014 в 16:47, контрольная работа

Краткое описание

1. Основные понятия и определения.
2. Общая схема решения функционального уравнения Беллмана.

Прикрепленные файлы: 1 файл

5fan_ru_Применение метода динамического программирования в задачах принятия решений.docx

Применение метода динамического программирования в задачах принятия решений.

1. Основные понятия и определения.

2. Общая схема решения функционального уравнения Беллмана.

1. Основные понятия и определения метода динамического программирования.

Динамическое программирование представляет собой совокупность процедур, используемых для оптимизации многошаговых процессов принятия решений. Вопросы динамического программирования были освещены в работах известных ученых (Вальда, Гирши), однако основной вклад в развитие теории многошаговых процессов внес американский математик Ричард Эрнст Беллман.

Беллманом был сформулирован принцип оптимальности и получено функциональное уравнение. Кроме того Беллман разработал схемы принятия решений на основе принципа оптимальности для многочисленных оптимизационных задач. Концептуально динамическое программирование применяется для анализа систем, которые характеризуются следующими признаками:

— процесс функционирования системы включает последовательные этапы, текущие этапы i, конечный этап m.

— на i-м шаге управляющее воздействие переводит систему из состояния Si-1, которое достигнуто на i-1 этапе в состояние Si.

— предполагается, что для системы выполняется принцип отсутствия последействия. Суть этого принципа заключается в том, что состояние Si зависит только от состояния системы на предыдущем этапе, то есть на Si-1, а так же зависит от управляющего воздействия Ui. И не зависит от предыдущих состояний системы и предыдущих управляющих воздействий.

— так же известна частная целевая функция или локальная Wi(Si, Ui), которая определяет значение критерия оптимальности, получаемого при применении на i-м этапе управляющего воздействия Ui и при нахождении системы в состоянии Si.

Критерий оптимальности функционирования системы за m этапов равен сумме локальных частных критериев, полученных на каждом из этапов.

Таким образом, при решении задач методом динамического программирования необходимо найти такой вектор управлений u=(u1,…ui…um), который обеспечит максимизацию суммарного критерия оптимальности.

Понятия таких терминов динамического программирования как этап, состояние системы, управляющее воздействие и локальный критерий оптимальности зависят от предметной ориентации системы. Для организационно-экономических систем в качестве этапов могут выступать интервалы планирования (год, квартал, месяц). В качестве состояний могут выступать наличие свободных финансовых средств на каждом этапе. Управляющее воздействие может быть представлено возможными вариантами инвестирования финансовых средств на каждом этапе. Локальный критерий оптимальности или локальный доход – это может быть прибыль, получаемая на каком-то этапе. Суммарный критерий оптимальности – это суммарная прибыль.

Если применить метод динамического программирования для дискретной системы принятия решений, например для задачи коммивояжера, под этапами можно понять переезд бригады между пунктами.

Для решения задач принятия решений методом динамического программирования может быть использовано два подхода:

— Первый подход предполагает, что одновременно находятся компоненты вектора управления для всех компонентов решения. Это метод глобальной оптимизации. Этот метод имеет существенный недостаток, который заключается в том, что при большой размерности вектора управления, существенно возрастают объем и трудоемкость вычислений.

— Второй подход базируется на нахождении оптимального управления последовательно для каждого из этапов. При этом если находить оптимальное воздействие для первого этапа и не учитывать при этом влияние управляющего воздействия на последующие решения, то итоговое оптимально решение может существенно отличаться от локального оптимального решения.

Классическая идея динамического программирования основана на реализации алгоритма обратной прогонки. W=

Суть этой идеи состоит в том, что в качестве этапа, для которого на первом шаге определяется локальное оптимальное управляющее воздействие. При таком подходе является неизвестным состояние, в котором может оказаться система перед началом выполнения последнего этапа. Поэтому локальное оптимальное управление необходимо рассматривать для всех возможных состояний, в которых может находиться система.

Как только мы определили локальные оптимальные управляющие воздействия для всех возможных состояний, начинается процесс оптимизации управления на предпоследнем этапе. Далее для каждого состояния предпоследнего этапа определяется оптимальное управляющее воздействие и эта процедура повторяется для всех последующих этапов в обратном порядке. Оптимальное решение для первого этапа определяется с учетом найденных оптимальных решений для последующих этапов.

2. Общая схема решения функционального уравнения.

Суть принципа Беллмана состоит в следующем:

Каково бы ни было состояние системы на i-м этапе, управляющее воздействие должно быть выбрано из условия, что на последующих этапах управление будет оптимальным. Дословно формулировка предложенная Беллманом звучит следующим образом: оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальные состояния и решения в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния полученного в результате первого решения.

Современная трактовка: Допущенную ошибку на начальных этапах нельзя исправить на последующих этапах решения.

Общая схема решения задач на основе принципа Беллмана предполагает формальное определение основных понятий процесса управления.

Первое понятие: этапы – количество этапов конечно. Качественное определение этапа зависит от природы системы и эти этапы связаны с процессом временной либо логической последовательности принятия решения.

Второе понятие: состояние системы – это набор параметров, который однозначно характеризует поведение системы. Состояние системы должно быть описано с той степени подробности, которая позволяет провести оценку текущих альтернативных решений.

Управление: это целенаправленное управляющее воздействие на i-м этапе принятия решения.

Условное оптимальное управление – наилучшая стратегия для каждого из состояний.

Оператор перехода – определяет условия перехода из одного состояния в другое, из состояния S в состояние S’. S’=

Локальный критерий оптимальности – это значение критерия оптимальности (величина прибыли), получаемое от функционирования системы на i-м этапе при условии, что система находилась в состоянии S и была выбрано управляющее воздействие Ui.

Условный суммарный критерий оптимальности – это значение критерия оптимальности (суммарный оптимальный доход), полученный от функционирования системы на i, i+1 и т.д. этапах работы.

Таким образом, с учетом принятых определений суммарный критерий оптимальности на i-м этапе для состояния S – это максимум суммы локального критерия.

В соответствии с алгоритмом обратной прогонки, решение функционального уравнения начинается с последнего этапа принятия решения, то есть полагается, что i=m. Тогда суммарная оптимальность будет определяться выражением.

В результате решения уравнения находится условное оптимальное управление для каждого состояния Um(S) и условный критерий оптимальности W(S). Найденные значения управляющего воздействия используются для решения функционального уравнения Беллмана при i=m-1.

В результате решения уравнения находится условное оптимальное управление Um(S) и условный критерий оптимальности W(S) на m-1 этапе. Таким образом, последовательное решение уравнения Беллмана позволяет определить пары условных оптимальных воздействий и условных оптимальных критериев на каждом шаге.

Для того, чтобы определить полное состояние системы, необходимо задать начальное состояние S0 и определить оптимальное управляющее воздействие U1(S0). После этого можно найти состояние системы исходя из этих данных.

– переход из 0-го в 1-е состояние

Формируем цепочку оптимальных состояний. Она выглядит следующим образом:

Принцип решения задачи динамического программирования с помощью уравнения Беллмана можно пояснить на примере задачи поиска кратчайшего пути в ориентированном графе. Для ориентированного графа известными являются вершины и дуги, длина пути в графе представляет собой сумму длин участков входящих в этот граф. В соответствии с алгоритмом в графе рассматриваются дуги для узлов с кратчайшими путями.

В задаче динамического программирования при использовании схемы прямой прогонки функциональное уравнение Беллмана имеет следующий вид:

— оператор обратного перехода устанавливающий состояние предыдущего этапа. Если провести аналогию с графом при разработке, то алгоритм прямой прогонки основан на том, что рассматриваются дуги, кратчайшие пути для которых известны.

Принцип оптимальности Беллмана. Решение задач методом динамического программирования

Автор работы: Пользователь скрыл имя, 16 Апреля 2012 в 08:25, реферат

Описание

За последние десятки лет, в прикладной математике большое внимание уделяется ново-му классу задач оптимизации, заключающихся в нахождении в заданной области, опреде-ляемой линейными и нелинейными ограничениями (равенствами и неравенствами), точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, применяемые в самых разнообразных областях человеческой деятельности, в которых необходим выбор одного из возможных образов действий, прежде всего в экономических исследованиях, при решении проблем управления и планирования производственных процессов, в проектирова-нии и перспективном планиро­вании и т. д.

Содержание

Введение 3
Принцип оптимальности Беллмана 4
Основной принцип динамического программирования 5
Примеры задач динамического программирования 7
Список используемых источников: 10

Работа состоит из 1 файл

Принцип оптимальности Беллмана 1111.docx

Принцип оптимальности Беллмана 4

Основной принцип динамического программирования 5

Примеры задач динамического программирования 7

Список используемых источников: 10

Введение

За последние десятки лет, в прикладной математике большое внимание уделяется новому классу задач оптимизации, заключающихся в нахождении в заданной области, определяемой линейными и нелинейными ограничениями (равенствами и неравенствами), точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, применяемые в самых разнообразных областях человеческой деятельности, в которых необходим выбор одного из возможных образов действий, прежде всего в экономических исследованиях, при решении проблем управления и планирования производственных процессов, в проектировании и перспективном планиро­вании и т. д.

Математическое программирование в настоящее время относится к числу наиболее интенсивно используемых дисциплин прикладной математики, потому соответствующий курс под тем или иным названием и в том или ином объеме включен в учебные планы почти всех вузов.

Важным разделом математического программирования является динамическое программирование, которые применяются в разных областях науки.

Этот способ очень удобен для решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой , выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной.

Чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы.

В 40-х годах 20 века, Ричард Эрнст Беллман, американский математик, впервые использовал словосочетание «динамическое программирование» для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей.

Принцип оптимальности Беллмана

Основной смысл подхода, реализуемого в динамическом программировании, заключен в замене решения исходной многомерной задачи последовательностью задач меньшей размерности.

Основные требования к задачам, выполнение которых позволяет применить данный подход:

• объектом исследования должна служить управляемая система (объект) с заданными допустимыми состояниями и допустимыми управлениями;
• задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия решения о выборе одного из допустимых управлений, приводящих к изменению состояния системы;
• задача не должна зависеть от количества шагов и быть определенной на каждом из них;
• состояние системы на каждом шаге должно описываться одинаковым (по составу) набором параметров;
• последующее состояние, в котором оказывается система после выбора решения на k-м. шаге, зависит только от данного решения и исходного состояния к началу k-го шага. Данное свойство является основным с точки зрения идеологии динамического программирования и называется отсутствием последействия.

Вопросы применения модели динамического программирования в обобщенном виде. Пусть стоит задача управления некоторым абстрактным объектом, который может пребывать в различных состояниях. Текущее состояние объекта отождествляется с некоторым набором параметров, обозначаемым в дальнейшем ξ и именуемый вектором состояния. Предполагается, что задано множество Ξ всех возможных состояний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляющие воздействия могут осуществляться в дискретные моменты времени k (k ∊ 1:n), причем управленческое решение заключа ется в выборе одного из управлений x_k ∊ Х. Планом задачи или стратегией управления называется вектор х = (х₁, х₂, . x_n-1), компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последовательными состояниями объекта ξ_k и ξ_k+1 существует известная функциональная зависимость, включающая также выбранное управление: ξ_k+1 = φ_k(x_k , ξ_k), k ∊ 1:п-1. Тем самым задание начального состояния объекта ξ₁ ∊ Ξ и выбор плана х однозначно определяют траекторию поведения объекта, как это показано на рис. 5.1.

Эффективность управления на каждом шаге k зависит от текущего состояния ξk , выбранного управления xk и количественно оценивается с помощью функций fk(хk, ξk), являющихся слагаемыми аддитивной целевой функции, характеризующей общую эффективность управления объектом. (Отметим, что в определение функции fk(хk, ξk) включается область допустимых значений хk , и эта область, как правило, зависит от текущего состояния ξk .) Оптимальное управление, при заданном начальном состоянии ξ1 , сводится к выбору такого оптимального планах*, при котором достигается максимум суммы значений fk на соответствующей траектории.

Основной принцип динамического программирования

Основной принцип динамического программирования заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции fk(хk, ξk), а выбирать

оптимальное управление хk* в предположении об оптимальности всех последующих шагов. Формально указанный принцип реализуется путем отыскания на каждом шаге k условных оптимальных управлений k(ξ), ξ ∊ Ξ, обеспечивающих наибольшую суммарную эффективность начиная с этого шага, в предположении, что текущим является состояние ξ.

Λk(ξ) максимальное значение суммы функций fk на протяжении шагов от k до п(получаемое при оптимальном управлении на данном отрезке процесса), при условии, что объект в начале шага k находится в состоянии ξ . Тогда функции Λk(ξ) должны удовлетворять рекуррентному соотношению:

где ξk+1 = φk(xk, ξ)

Соотношение (5.14) называют основным рекуррентным соотношением динамического программирования. Оно реализует базовый принцип динамического программирования, известный также как принцип оптимальности Беллмана:

F — Оптимальная стратегия управления должна удовлетворять следующему условию: каково бы ни было начальное состояние ξk на k-м шаге и выбранное на этом шаге управление хk,, последующие управления (управленческие решения) должны быть оптимальными по отношению к состоянию ξk+1 = φk(xk, ξk), получающемуся в результате решения, принятого на шаге k.

Основное соотношение (5.14) позволяет найти функции Λk(ξ) только в сочетании с начальным условием, каковым в нашем случае является равенство:

Сравнение рекуррентной формулы (5.14) с аналогичными соотношениями в рассмотренных выше примерах указывает на их внешнее различие. Это различие обусловлено тем, что в задаче распределения ресурсов фиксированным является конечное состояние управляемого процесса. Поэтому принцип Беллмана применяется не к последующим, а к начальным этапам управления, и начальное соотношение имеет вид:

Важно еще раз подчеркнуть, что сформулированный выше принцип оптимальности применим только для управления объектами, у которых выбор оптимального управления не зависит от предыстории управляемого процесса, т. е. от того, каким путем система пришла в текущее состояние. Именно это обстоятельство позволяет осуществить декомпозицию задачи и сделать возможным ее практическое решение.

В то же время, говоря о динамическом программировании как о методе решения оптимизационных задач, необходимо отметить и его слабые стороны. Так, в предложенной схеме решения задачи (5.3)-(5.4) существенным образом используется тот факт, что система ограничений содержит только одно неравенство, и, как следствие, ее состояние задается одним числом — нераспределенным ресурсом ξ . При наличии нескольких ограничений состояние управляемого объекта на каждом шаге характеризуется уже набором параметров ξ1, ξ2, . ξm , и табулировать значения функций Λk (ξ1, ξ2, . ξm) необходимо для многократно большего количества точек. Последнее обстоятельство делает применение метода динамического программирования явно нерациональным или даже просто невозможным. Данную проблему его основоположник Р. Беллман эффектно назвал «проклятием многомерности». В настоящее время разработаны определенные пути преодоления указанных трудностей.

Примеры задач динамического программирования

Одной из наиболее известных сфер приложения методов динамического программирования является такая область математической экономики, как теория управления запасами. Ее предметом является разработка и исследование математических моделей систем, занимающих промежуточное положение между источниками (производителями) тех или иных ресурсов и их потребителями. При математической формализации процессов управления запасами очень часто приходится использовать скачкообразные, не дифференцируемые и кусочно-непрерывные функции. Как правило, это обусловливается необходимостью учета эффектов концентрации, фиксированных затрат и платы за заказ. В связи с этим получаемые задачи с трудом поддаются аналитическому решению классическими методами, однако могут быть успешно решены с помощью аппарата динамического программирования. Рассмотрим достаточно типичную задачу, возникающую в процессе планирования деятельности системы снабжения, — так называемую динамическую задачу управления запасами.

Пусть имеется некоторая система снабжения (склад, оптовая база и т. п.), планирующая свою работу на п периодов. Ее деятельность сводится к обеспечению спроса конечных потребителей на некоторый продукт, для чего она осуществляет заказы производителю данного продукта. Спрос клиентов (конечных потребителей) в данной модели рассматривается как некоторая интегрированная величина, принимающая заданные значения для каждого из периодов, и он должен всегда удовлетворяться (т. е. не допускаются задолженности и отказы). Также предполагается, что заказ, посылаемый производителю, удовлетворяется им полностью, и временем между заказом и его выполнением можно пренебречь (т. е. рассматривается система с мгновенным выполнением заказа). Введем обозначения:

d_k — заранее известный суммарный спрос в k-м периоде;

х_k — заказ (поставка от производителя) в k-м периоде;

После получения поставки и удовлетворения спроса объем товара, подлежащего хранению в период k, составит ξ_k = y_k + х_k — d_k . Учитывая смысл параметра y_k , можно записать соотношение:

Расходы на получение и хранение товара в период k описываются функцией

Планом задачи можно считать вектор х = (х₁, х₂, . х_n), компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (5.24) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все п периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции:

Естественной в рамках сформулированной модели представляется задача нахождения последовательности оптимальных управлений (заказов) x*_k и связанных с ними оптимальных состояний (запасов) ξ*_k , которые обращают в минимум (5.25). В качестве начального условияиспользуем требование о сохранении после завершения управления заданного количества товара y_n+1 , а именно