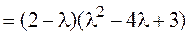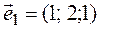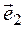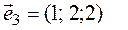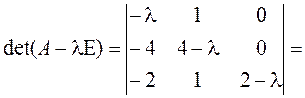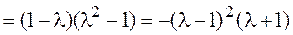Приведение к диагональному виду уравнения

Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду

Страницы работы

Фрагмент текста работы

§ 2. Приведение квадратной матрицы к диагональному виду

Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица 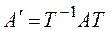– диагональная.

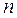
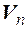
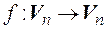
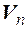
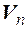
Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица -го порядка с элементами из поля P, – линейное пространство над Р, – тот линейный оператор, матрица которого в некотором базисе пространства совпадает с А, то для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в существовал базис, состоящий из собственных векторов оператора f.

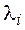
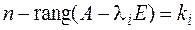
2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие

, (7)

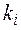
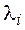
где – кратность корня характеристического уравнения матрицы А.

При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.

В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице 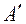, то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.

Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:

1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;

2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;

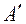
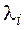
3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность;

4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;

5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .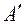

Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если

.

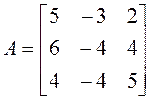
►Проводим решение по намеченному плану.

+

.

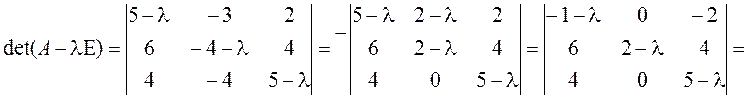
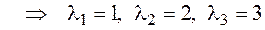
2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.

3. .

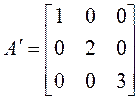
4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.

: ; ,

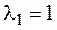
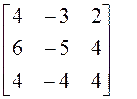
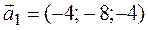
(алгебраические дополнения к элементам первой строки);

: ; =

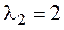
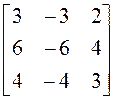
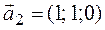
(алгебраические дополнения к элементам второй строки);

: ; ,

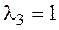
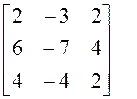
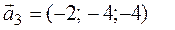
(алгебраические дополнения к элементам первой строки).

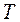
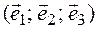
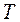
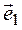
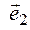
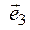
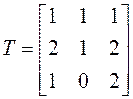
5. Составляем матрицу перехода от исходного базиса к, построенному базису , записывая в столбцы матрицы координатные столбцы векторов , и соответственно:

.◄

Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

.

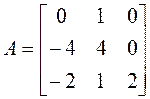
►Составляем и решаем характеристическое уравнение:

.

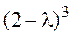
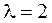
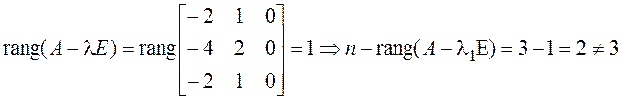
Матрица имеет только одно собственное значение , но его кратность равна трем. Проверяем выполнение условия (4.58):

.

Условие не выполняется, значит, матрица к диагональному виду не приводится.◄

Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

.

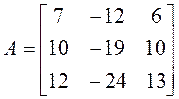
► Решение опять проводим по намеченному плану.

–

.

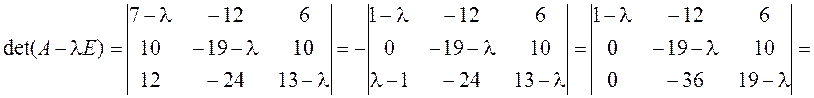
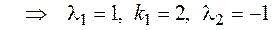
2. Проверяем выполнение условия (7) для кратного корня:

. (8)

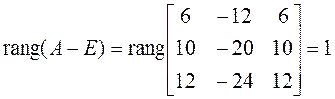
Таким образом, 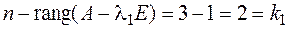, условие выполняется, матрица к диагональному виду приводится.

3. .

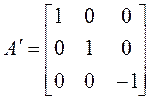
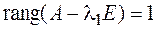
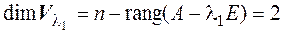
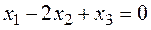
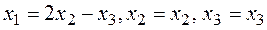
4. Так как , то , т. е для первого собственного значения можно найти два линейно независимых собственных вектора. По одной из строк матрицы (8), разделив все ее элементы на общий множитель, выписываем единственное уравнение для отыскания координат собственных векторов и решаем его: , . В качестве двух линейно независимых решений можно взять, например

риведение квадратичной формы к диагональному виду.

Определение. Пусть в евклидовом пространстве V 3 задана декартова система координат (x, y, z), k( ) – квадратичная форма, имеющая вид (12), A – её матрица.

Если в пространстве ввести другую систему координат, то тем же точкам будут соответствовать другие координаты, а значение функции в этих точках должно остаться прежним. Поэтому выражение (12) должно иметь другой вид. Пусть C – матрица перехода к новой системе координат (x¢, y¢, z¢), а A¢ – матрица квадратичной формы k( ) относительно новой системы. Тогда матрицы A и A¢ связаны между собой формулой

A¢= C Т AC. (11)

Если новые координаты тоже являются декартовыми, то C – ортогональная матрица, т.е. C Т = C — 1 ; в этом случае A¢= C — 1 AC. Именно по этому закону изменяется матрица линейного оператора при переходе к новому базису. Поэтому мы можем сопоставить квадратичной форме (10) оператор, A: V 3 ® V 3 определяемый матрицей A относительно системы координат (x, y, z). Тогда в любой декартовой системе координат квадратичная форма k( ) и поставленный ей в соответствие оператор будут иметь одинаковые матрицы (т.к. законы преобразования матриц одинаковы). Поскольку матрица A является симметрической, то оператор A будет самосопряженным.

Матрицу линейного оператора A можно привести к диагональному виду (5) с помощью выбора подходящего ортонормированного базиса B¢= <, , >. Если сохранить прежнее начало координат, то этот базис оп-ределит в пространстве новую систему координат (x¢, y¢, z¢), относительно которой матрица квадратичной формы будет иметь такой же диагональный вид, а, значит, сама квадратичная форма будет иметь диагональный вид

В задачах на приведение квадратичной формы к каноническому виду обязательно нужно выписать формулы перехода от старых координат (x, y, z) к новым координатам (x¢, y¢, z¢):

X¢= C — 1 X, (14)

или формулы перехода от новых координат к старым:

где C – матрица перехода, а X и X¢ – координатные столбцы:

Напомним, если переход от одного аффинного базиса B = <, , >к другому аффинному базису B¢= <, , >осуществляется по формулам

= c₁ 1 + c₁ 2 + c₁ 3 ,

то матрица C составляется следующим образом:

C = , (16)

Тогда в развернутом виде формулы (14¢) имеют вид:

x = c₁ 1 x¢ + c₂ 1 y¢ + c₃ 1 z¢,

Предположим, что старая и новая системы координат являются декартовыми. Тогда, как уже отмечалось, матрица C перехода от старой системы координат к новой будет ортогональной, т.е. C Т = C — 1 . Поэтому формулы (14) принимают вид X¢= C Т X и составляются особенно просто:

x¢= c₁ 1 x + c₁ 2 y + c₁ 3 z,

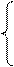
Для решения задач, связанных с приведением уравнения поверхности второго порядка к каноническому виду, нам понадобятся именно формулы (14¢), выражающие старые координаты через новые.

Пример 3.В пространстве V 3 квадратичная форма k() определяется относительно декартовой системы координат (x, y, z) формулой

С помощью выбора новой системы координат (x¢, y¢, z¢) привести k() к диагональному виду.

Решение. Составим матрицу квадратичной формы k() относительно системы координат (x, y, z). Имеем 3 = a₂₂, 4 = 2a₁₂, -2 = 2a₁₃, — 4 = 2a₂₃, а т.к. x 2 и y 2 отсутствуют, то a₁₁= a₃₃ = 0. Итак,

A = .

Мы видим, что матрица A совпадает с матрицей из примера 2, находим собственные числа и соответствующие им собственные векторы

Тогда, если выбрать новую систему координат (x¢, y¢, z¢) с тем же началом, но определяемую базисом B¢= <, , >, то квадратичная форма k( ) примет диагональный вид

Новые координаты выражаются через старые по формулам:

x¢= x + z,

Старые координаты выражаются через новые по формулам:

x = x¢ + y¢ + z¢,