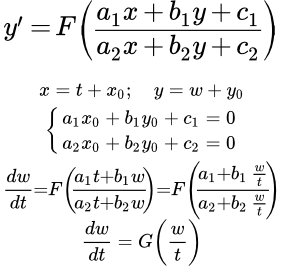Приведение к однородному дифференциальному уравнению первого порядка путем

Дифференциальные уравнения первого порядка, приводящиеся к однородным

К однородным уравнениям первого порядка приводится уравнение вида:
(1) ,
где f – функция.

Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
a ₁ x + b ₁ y + c ₁ , a ₂ x + b ₂ y + c ₂ ,
и выполнить замену:
a ₁ x + b ₁ y + c ₁ → t ( a ₁ x + b ₁ y + c ₁ ) ;
a ₂ x + b ₂ y + c ₂ → t ( a ₂ x + b ₂ y + c ₂ ) .
Если, после преобразований, t сократится, то это уравнение приводится к однородному.

Пример

Определить, приводится ли данное дифференциальное уравнение к однородному:
.

Выделяем две линейные формы:
x + 2 y + 1 и x + 4 y + 3 .
Первую заменим на t ( x + 2 y + 1) , вторую – на t ( x + 4 y + 3) :
.
По свойству логарифма:

.
t сокращается:
.
Следовательно, это уравнение приводится к однородному.

Решение дифференциального уравнения, приводящегося к однородному уравнению

Решаем систему уравнений:
(2)

Здесь возможны три случая.

1) Система (2) имеет бесконечное множество решений (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 совпадают). В этом случае
;
.
Тогда
.
Это простейший вид уравнения с разделяющимися переменными:
.
Его решение:
y = Ax + C .

2) Система (2) не имеет решений (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 параллельны). В этом случае a ₁ b ₂ = a ₂ b ₁ .
Применим это соотношение.

.

Это означает, что a ₂ x + b ₂ y + c ₂ является функцией от a ₁ x + b ₁ y + c ₁ . Поэтому является функцией от a ₁ x + b ₁ y + c ₁ . То есть f является функцией от a ₁ x + b ₁ y + c ₁ . Обозначим такую функциею как g . Тогда исходное уравнение (1) имеет вид:
.
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой
z = a ₁ x + b ₁ y + c ₁ .

3) Система (2) имеет одно решение (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 пересекаются в одной точке). Обозначим это решение как x ₀ , y ₀ . Тогда
(3)
Делаем подстановку x = t + x ₀ , y = u + y ₀ , где u – это функция от t . Тогда
dx = dt, dy = du ;

.
Или
.
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = z t , где z – это функция от t .

Пример решения дифференциального уравнения, приводящегося к однородному уравнению первого порядка

Решить уравнение
(П.1) .

1) Проверим, приводится ли это дифференциальное уравнение к однородному. Для этого выделяем две линейные формы:
2 x – y + 4 и x – 2 y + 5 .
Первую заменим на t (2 x – y + 4) , вторую – на t ( x – 2 y + 5) :
.
Делим на t :
.
t сократилось, поэтому это уравнение приводится к однородному.

2) Решаем систему

Из первого уравнения y = 2 x + 4 . Подставляем во второе:
x – 2(2 x + 4) + 5 = 0 ;
x – 4 x – 8 + 5 = 0 ;
– 3 x = 3 ;
x = – 1 ;
y = 2 x + 4 = 2·(–1) + 4 = 2 .
Итак, мы нашли решение системы:
x ₀ = –1 , y ₀ = 2 .

3) Делаем подстановку:
x = t + x ₀ = t – 1 ;
y = u + y ₀ = u + 2 ,
где u – функция от t . dx = dt, dy = du , ;
;
.
Подставляем в (П.1):
(П.2) .
Это – однородное уравнение.

4) Решаем однородное уравнение (П.2). Делаем подстановку:
u = z · t , где z – функция от t .
u′ = ( z · t ) ′ = z′t + z t′ = z′t + z .
Подставляем в (П.2):
.
Сокращаем на t и выполняем преобразования:
;
;
.
Разделяем переменные – умножаем на dt и делим на t ( z 2 – 1) . При z 2 ≠ 1 получаем:
.
Интегрируем:
(П.3) .
Вычисляем интегралы:
;

.
Подставляем в (П.3):
.
Умножим на 2 и потенцируем:
;
.
Заменим постоянную e 2 C → C . Раскроем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C . Умножим на ( z + 1) 2 и применим формулу: z 2 – 1 = ( z – 1)( z + 1) .
.
Сократим на ( z – 1) :
.
Возвращаемся к переменным u и t , используя формулу: u = z t . Для этого умножим на t :
;
;
.
Возвращаемся к переменным x и y , используя формулы: t = x + 1 , u = y – 2 .
;
(П.4) .

Теперь рассмотрим случай z 2 = 1 или z = ±1 .
;
.
Для верхнего знака «+» имеем:
;
.
Это решение входит в общий интеграл (П.4) при значении постоянной C = 0 .
Для нижнего знака «–»:
;
.
Эта зависимость также является решением исходного дифференциального уравнения, но не входит в общий интеграл (П.4). Поэтому к общему интегралу добавим решение
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 30-07-2012 Изменено: 22-06-2015

Дифференциальные уравнения, приводимые к уравнениям первого порядка

Вы будете перенаправлены на Автор24

Дифференциальные уравнения второго порядка, в которых правая часть не зависит от неизвестной функции и её производной

Таким дифференциальным уравнением второго порядка является уравнение вида $y»=f\left(x\right)$. В нем правая часть не зависит от неизвестной функции $y$ и её производной $y’$, а зависит только от $x$. Решается это уравнение последовательным интегрированием.

Представим его в таком виде: $\frac \left(y’\right)=f\left(x\right)$, откуда $d\left(y’\right)=f\left(x\right)\cdot dx$.

Интегрируем первый раз, используя то свойство, что неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: $\int d\left(y’\right) =\int f\left(x\right)\cdot dx $ или $y’=\int f\left(x\right)\cdot dx +C_ <1>$, где $C_ <1>$ — произвольная постоянная.

Таким образом, дифференциальное уравнение второго порядка сведено теперь к дифференциальному уравнению первого порядка, которое можно представить в таком виде: $dy=\left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx$.

Интегрируем полученное дифференциальное уравнение повторно: $y=\int \left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx =\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +\int C_ <1>\cdot dx$. Окончательно получаем:$y=\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +C_ <1>\cdot x+C_ <2>$, где $C_ <2>$ — произвольная постоянная.

Процесс интегрирования завершен. Получена неизвестная функция $y$, которая является общим решением данного дифференциального уравнения второго порядка.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x\right)$ может быть представлен в следующем виде:

1. находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx $ и записываем первую производную искомой функции в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$;
2. находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx $ и записываем окончательно общее решение данного дифференциального уравнения: $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$;
3. для поиска частного решения начальные условия подставляем в выражение для первой производной $y’$, а также в общее решение; в результате находим значения произвольных постоянных $C_ <1>$ и $C_ <2>$.

Готовые работы на аналогичную тему

Найти общее решение дифференциального уравнения второго порядка $y»=4$. Записать также его частное решение, которое удовлетворяет начальным условиям $y=1$ при $x=1$, $y’=1$ при $x=1$.

В данном дифференциальном уравнении правая часть не зависит ни от неизвестной функции $y$, ни от её производной $y’$. Следовательно, оно решается последовательным интегрированием два раза подряд.

Находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx =\int 4\cdot dx =4\cdot x$. Записываем выражение для первой производной в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$, то есть $y’=4\cdot x+C_ <1>$.

Находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx =\int 4\cdot x\cdot dx =2\cdot x^ <2>$. Записываем окончательно общее решение в виде $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$. Получаем: $y=2\cdot x^ <2>+C_ <1>\cdot x+C_ <2>$.

Ищем частное решение. Подставляем начальное условие $y’=1$ при $x=1$ в выражение для $y’$: $1=4\cdot 1+C_ <1>$, откуда $C_ <1>=-3$. Подставляем начальное условие $y=1$ при $x=1$ в выражение для $y$: $1=2\cdot 1^ <2>+\left(-3\right)\cdot 1+C_ <2>$, откуда $C_ <2>=2$. Таким образом, частное решение имеет вид: $y=2\cdot x^ <2>-3\cdot x+2$.

Дифференциальные уравнения второго порядка, не содержащие неизвестной функции

Указанные дифференциальные уравнения второго порядка допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее неизвестной функции $y$, имеет вид $y»=f\left(x,y’\right)$.

Для его решения применяют замену $y’=z\left(x\right)$.

При этом $y»=z’\left(x\right)$. После подстановки данное дифференциальное уравнение приобретает вид дифференциального уравнения первого порядка относительно $z$, то есть $z’=f\left(x,z\right)$. Решая его, находим $z\left(x\right)=\phi \left(x,C_ <1>\right)$.

В свою очередь, поскольку $y’=z\left(x\right)$, то $y’=\phi \left(x,C_ <1>\right)$. Это также дифференциальное уравнение первого порядка, которое допускает непосредственное интегрирование. Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_ <1>\right)\cdot dx +C_ <2>$.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x,y’\right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=\phi \left(x,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, которое допускает непосредственное интегрирование;
4. находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx $ и получаем общее решение в виде $y=I+C_ <2>$.

Найти общее решение дифференциального уравнения$y»-\frac =3\cdot x$.

Данное дифференциальное уравнение не содержит неизвестной функции $y$, поэтому переписываем его в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$. Получаем: $z’-\frac =3\cdot x$.

Это дифференциальное уравнение первого порядка является линейным неоднородным, решая которое известным методом, получаем $z=\left(3\cdot x+C_ <1>\right)\cdot x$.

Найденное решение представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, то есть $y’=\left(3\cdot x+C_ <1>\right)\cdot x$. Это дифференциальное уравнение допускает непосредственное интегрирование.

Находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx =\int \left(3\cdot x+C_ <1>\right)\cdot x\cdot dx =x^ <3>+C_ <1>\cdot \frac > <2>$ и получаем общее решение в виде $y=I+C_ <2>=x^ <3>+C_ <1>\cdot \frac > <2>+C_ <2>$. Это общее решение можно представить также в виде $y=x^ <3>+C_ <1>\cdot x^ <2>+C_ <2>$.

Дифференциальные уравнения второго порядка, не содержащие независимой переменной

Указанные дифференциальные уравнения второго порядка также допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее независимой переменной $x$, имеет вид $y»=f\left(y,y’\right)$.

Для его решения применяют замену $y’=z\left(y\right)$.

Подставляем выражения для $y’$ и $y»$ в данное дифференциальное уравнение: $z\cdot \frac =f\left(y,z\right)$. Получили дифференциальное уравнение первого порядка относительно переменной $z$, которая является функцией $y$. Решая его, находим $z\left(y\right)=\phi \left(y,C_ <1>\right)$.

В свою очередь, поскольку $\frac =z\left(y\right)$, то $\frac =\phi \left(y,C_ <1>\right)$. Полученное дифференциальное уравнение представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными, общее решение которого можно найти из выражения $\int \frac <\phi \left(y,C_<1>\right)> =x+C_ <2>$.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(y,y’\right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z\cdot z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=\phi \left(y,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $\frac=\phi \left(y,C_ <1>\right)$, которое является дифференциальным уравнением с разделяющимися переменными;
4. находим интеграл $I=\int \frac<\phi \left(y,C_<1>\right)> $ и получаем общее решение в виде $I=x+C_ <2>$.

Однородные дифференциальные уравнения
и приводящиеся к ним

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.