Приведение уравнения к виду удобному для итераций

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .

Приведение СЛАУ к виду, удобному для итераций.

ЗАДАНИЕ №1

ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

(решение трансцендентных и алгебраических уравнений)

Характеристическое уравнение системы автоматического управления (САУ) режимами работы электрических систем в общем случае имеет нелинейный вид. Решаются такие уравнения, как правило, численными методами.

В задании №1 необходимо решить два нелинейных уравнения (трансцендентное и алгебраическое).

1. Графически отделить корни.

2. Уточнить корни уравнений численными методами согласно варианту задания (по одному корню для каждого уравнения).

3. Проверить решение трансцендентного уравнения при помощи встроенного в MathCAD блока решений Given-Minerr, арешение алгебраического уравнения – встроенной в MathCAD функцией polyroots().

Указания к выполнению задания

Для графического отделения корней в MathCAD строится график функции , составленной на основе исходного уравнения.

Например, дано трансцендентное уравнение:

.

Для составления функции переносим все слагаемые в правую часть, получим:

.

Отделение корней состоит в определении интервалов [a,b], в котором график функции один раз пересекает ось абсцисс (интервалы изоляции корня).

Алгоритмы методов уточнения корней.

Метод половинного деления.

1) Исходные данные: интервал [a,b], заданная погрешность расчета 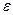. Для этого и последующих заданий можно принять .

2) Рассчитать: .

3) Приближенное значение корня:

. (*)

4) Рассчитать .

5) Если или , то — корень, полученный с заданной точностью (окончание расчета).

при и переход к (*);

при , и переход к (*).

Метод хорд.

1) Исходные данные: интервал [a,b], заданная погрешность расчета .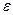

2) Определить первую и вторую производные функции — и .

3) Рассчитать: , , ;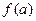

, , .

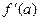
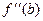
4) Определить дополнительные величины , и :

— минимальное значение из и ;

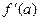
если 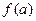и имеют одинаковый знак, то , ,

иначе , .

5) Рассчитать: , .

6) Приближенное значение корня:

. (*)

7) Рассчитать .

Если , то — корень, полученный с заданной точностью (окончание расчета).

Если нет, то: , и переход к (*).

Метод касательных.

1) Исходные данные: интервал [a,b], заданная погрешность расчета .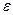

2) Определить первую и вторую производные функции — и .

3) Рассчитать: , , ;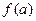

, , .

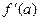
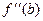
4) Определить дополнительные величины , и :

— минимальное значение из и ;

— максимальное значение из и ;

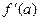
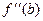
если 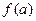и имеют одинаковый знак, то , иначе .

5) Приближенное значение корня:

. (*)

6) Если , то — корень, полученный с заданной точностью (окончание расчета). Если нет, то: и переход к (*).

ЗАДАНИЕ №2

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)

В результате применения законов Кирхгофа к расчету электрических цепей постоянного тока получают систему линейных алгебраических уравнений, которая связывает между собой параметры цепи и параметры режима.

Решают СЛАУ различными методами, в частности – итерационными.

В задании №2 необходимо решить систему линейных алгебраических уравнений методом ускоренной итерации (метод Зейделя).

1. Привести СЛАУ к виду, удобному для итераций.

2. Преобразованную (эквивалентную) систему привести к нормальному виду.

3. Принять за начальные приближения свободные члены нормализованных уравнений системы.

4. Решить СЛАУ (согласно варианту задания) с точностью .

5. Проверить решение СЛАУ при помощи встроенной в MathCAD функции lsolve().

Указания к выполнению задания

Приведение СЛАУ к виду, удобному для итераций.

Для обеспечения сходимости итерационного процесса достаточно, чтобы для исходной системы модули диагональных коэффициентов каждого уравнения были больше суммы модулей всех остальных коэффициентов в этом же уравнении. Приведение исходной системы к эквивалентной, для которой выполняются условия сходимости, делается с помощью элементарных преобразований.

Например, для системы из трех уравнений:

.

Если , и — сходимость итерационного процесса обеспечена.

Привести к виду, удобному для итераций, систему:

.

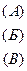
Просматриваем уравнения: в уравнении (Б) — следовательно, принимаем уравнение (Б) в качестве второго уравнения эквивалентной системы.

В уравнении (А) — принимаем уравнение (А) в качестве третьего уравнения исходной системы.

За первое уравнение эквивалентной системы примем комбинацию (2·В+А), тогда получим:

,

.

В итоге получаем эквивалентную систему уравнений, удобную для итераций:

.

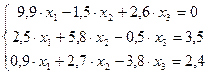
Решение СЛАУ методом простой итерации

Назначение сервиса . Онлайн-калькулятор предназначен для решения СЛАУ методом простой итерации в онлайн режиме (см. пример решения). Для проверки решения генерируется шаблон в Excel .

• Шаг №1
• Шаг №2
• Видеоинструкция

Рассмотрим достаточные условия сходимости итерационной последовательности n>.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ₁: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ₂: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ₃: , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).

Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

Последовательные приближения будем искать по формулам:

Получаем:
x 1 =(-1.9022; 0.4889; 2.1456), x 2 =(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ₁ вычисляем коэффициент μ
.
Вычисляем погрешность:

При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.

Метод итераций для системы уравнений в Excel

Для вычисления точности epsilon .
Итерация №1: =ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2: =ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.