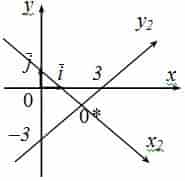
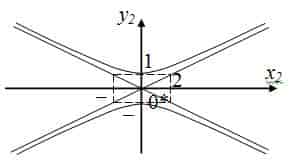
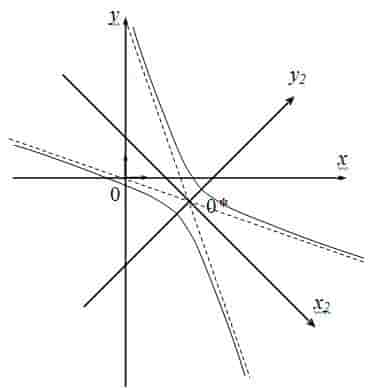
Приведение уравнения линии 2 порядка

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Приведение уравнений линий и поверхностей второго порядка к каноническому виду

Страницы работы

Содержание работы

§. 5. Приведение уравнений линий и поверхностей

второго порядка к каноническому виду

Известно, что для любой квадратичной формы на конечном действительном евклидовом пространстве в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид. Используя этот факт, любую линию или поверхность второго порядка можно привести к каноническому виду по следующему плану.

1. Для квадратичной части уравнения (т. е. квадратичной формы) находим канонический вид и ортогональное преобразование переменных, приводящее квадратичную форму к этому каноническому виду.

2. Подставляем выражение старых переменных через новые в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, в котором коэффициенты при квадратах совпадают с собственными значениями ее матрицы, свободный член не меняется, линейная часть преобразуется непосредственно.

3. Получили уравнение, не содержащее произведений переменных. С помощью преобразования параллельного переноса избавляемся от лишних слагаемых первых степеней и тем самым окончательно приводим уравнение к каноническому виду.

Если линия или поверхность второго порядка имеет центр симметрии, то решение задачи можно существенно упростить, поменяв местами 1-й и третий пункты, а второй тогда совсем исчезает.

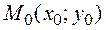
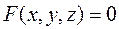
Для того чтобы точка была центром симметрии поверхности второго порядка , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений

(5. 3)

Если с помощью параллельного переноса поместить начало координат в центр симметрии поверхности второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле

. (5.4)

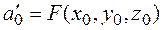
Аналогичные утверждения справедливы и для линий второго порядка (подробно обоснование см., например, в []).

Пример 1. Определить вид линии второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту линию, если ее уравнение имеет вид

. (5.5)

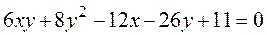
►В первую очередь проверим, имеет ли эта линия центр симметрии. Составляем систему линейных уравнений (5.3)

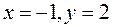
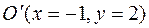
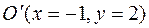
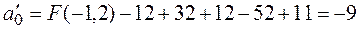
из которой находим: . Поместим с помощью параллельного переноса начало координат в точку (если в задаче используются несколько систем координат, то обязательно надо указывать, в какой именно из них вы даете координаты точки). По формуле (5.4) (подставляем координаты в левую часть (5.5)) находим . После преобразования параллельного переноса уравнение линии примет вид .

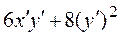
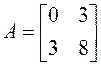
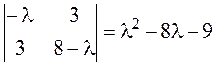
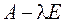
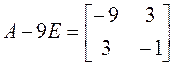
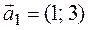
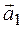
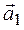
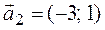
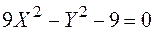
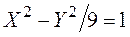
Теперь приведем к каноническому виду квадратичную часть уравнения (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:

, , .

Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей при : , . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора и в одной из них поменяв знак. Итак, . Применим ортогональное преобразование, в результате которого оси новой системы координат будут направлены по собственным векторам. После этого уравнение примет вид (коэффициенты при квадратах совпадают с найденными собственными значениями) , или , которое задает гиперболу с полуосями 1 и 3 и осью в качестве действительной.

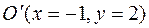
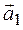
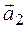
Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. Намечаем новое начало координат – точку . От этой точки откладываем собственные векторы и , которые задают направление новых осей. В полученной системе координат рисуем полученную гиперболу (рис.5.1). ◄

Замечания. 1. При таком способе решения нет необходимости выписывать ни преобразование параллельного переноса, ни ортогональное преобразование, т. к. мы и без непосредственной подстановки их в уравнение знаем, как оно преобразуется. Нет необходимости даже собственные векторы нормировать: ортогональное преобразование не нужно, а векторы с целочисленными координатами легче рисовать. Именно поэтому задачу приведения линии второго порядка к каноническому виду в том случае, когда эта линия имеет центр симметрии, сложной не назовешь.

Исследование уравнений второго порядка

Преобразование координат в уравнении второго порядка.

В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ <2>+ 2Bxy + Cy^ <2>+ 2Dx + 2Ey + F = 0,\label
$$
в котором коэффициенты \(A\), \(B\) и \(C\) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения \eqref не изменится.

При повороте базиса декартовой прямоугольной системы координат на угол \(\varphi\) старые координаты точки \(x\), \(y\) будут связаны с ее новыми координатами \(x’\), \(y’\) формулами
$$
x = x’\cos \varphi-y’\sin \varphi,\\ y = x’\sin \varphi + y’\cos \varphi.\nonumber
$$
В новых координатах уравнение \eqref примет вид
$$
A(x’\cos \varphi-y’\sin \varphi)^ <2>+ 2B(x’\cos \varphi-y’\sin \varphi) \times \\ \times (x’\sin \varphi + y’\cos \varphi) + C(x’\sin \varphi + y’\cos \varphi) + … = 0.\nonumber
$$
Здесь многоточием обозначены члены первой степени относительно \(x’\), \(y’\) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением \(x’y’\) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при \(x’y’\) есть
$$
B’ = -A\sin \varphi \cos \varphi + B(\cos^<2>\varphi-\sin^<2>\varphi) + C\sin \varphi \cos \varphi.\nonumber
$$
Если \(B = 0\), то поворачивать систему координат не будем. Если же \(B \neq 0\), то выберем угол \(\varphi\) так, чтобы \(B’\) обратилось в нуль.

Это требование приведет к уравнению
$$
2B \cos 2\varphi = (A-C)\sin 2\varphi.\label
$$
Если \(A = C\), то \(\cos 2\varphi = 0\), и можно положить \(\varphi = \pi/4\). Если же \(A \neq C\), то выбираем \(\varphi = \displaystyle\frac<1> <2>\operatorname \left[\frac<2B>\right]\). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ <\ 2>+ C’y’^ <\ 2>+ 2D’x’ + 2E’y’ + F’ = 0.\label
$$
Выражения для коэффициентов уравнения \eqref через коэффициенты \eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.

Если в уравнение \eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.

В самом деле, пусть, например, \(A’ \neq 0\). Перепишем \eqref в виде
$$
A’\left(x’^ <\ 2>+ \frac<2D’>x’ + \frac>>\right) + C’y’^ <\ 2>+ 2E’y’ + F’-\frac = 0.\nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами \(x″ = x’ + D’/A’\), \(y″ = y’\), то уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ 2E’y″ + F″ = 0,\nonumber
$$
как и требовалось.

Канонические виды уравнений второго порядка.

Предположим, что \(A’C’ \neq 0\), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ F″ = 0.\label
$$

Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.

Случай A’C’ > 0.

Если \(A’C’ > 0\), то коэффициенты \(A’\) и \(C’\) имеют один знак. Для \(F″\) имеются следующие три возможности.

Знак \(F″\) противоположен знаку \(A’\) и \(C’\). Перенесем \(F″\) в другую часть равенства и разделим на него. Уравнение примет вид
$$
\frac>> + \frac>> = 1,\label
$$
где \(a^ <2>= -F″/A’\), \(b^ <2>= -F″/C’\). Можно считать, что в этом уравнении \(a > 0\), \(b > 0\) и \(a \geq b\). Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат
$$
x^ <*>= y″,\ y^ <*>= x″.\label
$$

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(a \geq b\), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.

При \(a = b\) уравнение \eqref есть уравнение окружности радиуса \(a\). Таким образом, окружность — частный случай эллипса.

Случай A’C’ Определение.

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.

Случай \(A’C’ = 0\).

Допустим теперь, что \(A’C’ = 0\), и, следовательно, один из коэффициентов \(A’\) или \(C’\) равен нулю. В случае необходимости, делая замену \eqref, мы можем считать, что \(A’ = 0\). При этом \(C \neq 0\), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ <\ 2>+ 2D’x″ + F″ = 0.\nonumber
$$

Пусть \(D’ \neq 0\). Сгруппируем члены следующим образом:
$$
C’y″^ <\ 2>+ 2D’\left(x″ + \frac<2D’>\right) = 0.\nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода \(x^ <*>= x″ + F″/2D’\), \(y^ <*>= y″\). Тогда уравнение примет вид
$$
C″y^ <*2>+ 2D’x^ <*>= 0,\nonumber
$$
или
$$
y^ <*2>= 2px^<*>,\label
$$
где \(p = -D’/C″\). Мы можем считать, что \(p > 0\), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: \(\tilde = -x^<*>\), \(\tilde = y^<*>\).

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(p > 0\), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.

Допустим, что \(D’ = 0\). Уравнение имеет вид \(C’y″^ <\ 2>+ F″ = 0\). Относительно \(F″\) есть следующие три возможности.

1. Если \(C’F″ 0\) знаки \(C’\) и \(F″\) совпадают. Разделив на \(C’\), приведем уравнение к виду
   $$
   y″^ <\ 2>+ a^ <2>= 0.\label
   $$
   Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду \eqref, называют уравнением пары мнимых параллельных прямых.
2. Остался последний случай \(F″ = 0\). После деления на \(C’\) уравнение принимает вид
   $$
   y″^ <\ 2>= 0.\label
   $$
   Это уравнение эквивалентно уравнению \(y″ = 0\), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду \eqref, называется уравнением пары совпавших прямых.

Теперь мы можем объединить всё вместе.

Пусть в декартовой системе координат задано уравнение второго порядка \eqref.

Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:

1. Уравнение эллипса.
   $$
   \frac>> + \frac>> = 1;\nonumber
   $$
2. Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
   $$
   \frac>> + \frac>> = -1;\nonumber
   $$
3. Уравнение пары мнимых пересекающихся прямых (точка).
   $$
   a^<2>x^ <2>+ c^<2>y^ <2>= 0;\nonumber
   $$
4. Уравнение гиперболы.
   $$
   \frac>>-\frac>> = 1;\nonumber
   $$
5. Пересекающиеся прямые.
   $$
   a^<2>x^<2>-c^<2>y^ <2>= 0;\nonumber
   $$
6. Уравнение параболы.
   $$
   y^ <2>= 2px;\nonumber
   $$
7. Пара параллельных прямых.
   $$
   y^<2>-a^ <2>= 0;\nonumber
   $$
8. Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
   $$
   y^ <2>+ a^ <2>= 0;\nonumber
   $$
9. Прямая (пара совпавших прямых).
   $$
   y^ <2>= 0.\nonumber
   $$