Приведение уравнения линии к общему каноническому виду

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

3.8. Приведение уравнения к каноническому виду

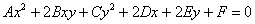
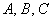
Эта задача следовала за нами практически с самого начала главы и в заключительном параграфе мы окончательно разберёмся, как общее уравнение линии второго порядка ( не равны одновременно нулю) свести к одному из девяти канонических случаев.

В предыдущих параграфах мы очень подробно отработали частный случай уравнения, когда коэффициент :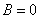
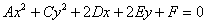
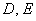
(не равны нулю одновременно)

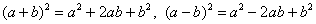
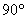
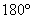
Такое уравнение приводится методом выделения полного квадрата(ов) с дальнейшим применением формул , далее осуществляется поворот (опционально) на угол либо в некоторых случаях на и непременно параллельный перенос линии или системы координат.

…У вас такое уравнение? Значит, вам хватит материалов предыдущих параграфов!

Не такое? Значит, не хватит 🙂

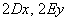
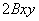
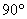
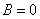
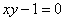
Как многие подметили, члены общего уравнения «отвечают» за параллельный перенос, и логично предположить, что ненулевое слагаемое «отвечает» за поворот (за исключением угла и кратных ему углов, при которых , и мы отделываемся лёгким испугом).Простейший пример поворота на «нехалявный» угол нам уже встречался – это неканонически расположенная «школьная» гипербола .

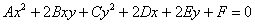
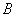
Уравнение с ненулевым коэффициентом неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.

Рассмотрим в качестве примера уравнение 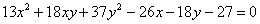. Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?

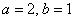
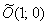
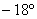
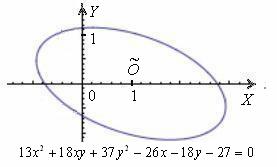
Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс с полуосями , который расположен центром в точке и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно :
Мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс.

Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает.
Выше я рассматривал два способа приведения. Применительно к нашему примеру:

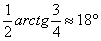
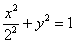
1) Осуществим параллельный перенос эллипса центром в начало координат (представляем мысленно) и повернём его на угол (против часовой стрелки). В результате получится нужное уравнение .

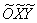
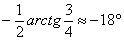
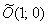
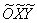
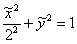
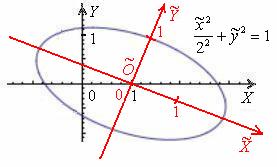
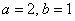
2) Перейдём к прямоугольной системе координат , которая получается путём поворота исходной системы координат на вокруг начала координат и её параллельного переноса центром в точку . Таким образом, в новой системе координат уравнение данного эллипса запишется в каноническом виде :
«Навскидку» второй способ кажется вычурным и неуклюжим, однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию, какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями , своими фокусами и другими индивидуальными характеристиками.

Но стОит ли перемещать САМУ линию? Представьте, что крыша вашего дома имеет эллиптическую форму, и шаловливый Карлсон выбрал начало координат на трубе кочегарки J. Что вы будете делать, чтобы с комфортом исследовать эллипс? Разумеется, не станете переносить крышу, а перейдёте к удобной системе координат.

То есть, система координат относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно её, а не «уникальный» эллипс, крышу дома или что-то ещё.

А суть преамбулы состоит в том, что далее мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид.

Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки.

Для этого нам потребуется ещё одно теоретическое понятие:

Все линии 2-го порядка можно разделить на две большие группы:

1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых);

2) нецентральные линии, у которых центры симметрии отсутствуют (парабола), либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых).

Итак, вы счастливый обладатель уравнения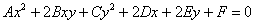
с ненулевым коэффициентом .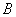

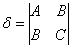
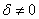
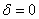
С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель . Если , то перед нами уравнение центральной линии, если же – то нецентральной.

Для уравнения :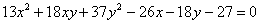
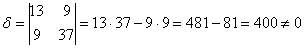
, значит, оно определяет центральную линию.

Зачем это нужно? Чтобы выбрать наиболее выгодный способ решения. Да, конечно, ваш учебный план может и не предоставить возможность выбора, но, тем не менее, я постараюсь провести вас через дебри самой комфортной и короткой тропинкой.

Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения либо ортогональное преобразование квадратичной формы (но тут уже надо ориентироваться в другой теме). Сначала разберём одно, затем другое, и даже если вам нужно разделаться лишь с нецентральной линией, постарайтесь не пропускать нижеследующий параграф, поскольку вся информация взаимосвязана:

Приведение к каноническому виду линейных уравнений с частными производными второго порядка

Федеральное агентство по образованию

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики, экономики и информатики

Кафедра дифференциальных и интегральных уравнений

ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………

1.1. Необходимый теоретический материал………………………..

1.2. Пример выполнения задачи1 (приведение к

каноническому виду уравнений гиперболического типа) .

1.3. Пример выполнения задачи 2 (приведение к

каноническому виду уравнений параболического типа)

1.4. Пример выполнения задачи 3 (приведение к

каноническому виду уравнений эллиптического типа) ..

1.5. Задачи для самостоятельного решения ………………….….

Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2.1. Необходимый теоретический материал …………………..

2.2. Пример выполнения задачи 4

2.3. Задачи для самостоятельного решения ……………………..

В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.

Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.

§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.

Задача. Определить тип уравнения

(1)

и привести его к каноническому виду.

1.1. Необходимый теоретический материал.

I. Тип уравнения (1) определяется знаком выражения :

· если в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.

Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.

Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение является уравнением эллиптического типа в точках ; параболического типа в точках ; и гиперболического типа в точках .

II. Чтобы привести уравнение к канонического виду, необходимо:

1. Определить коэффициенты ;

2. Вычислить выражение ;

3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );

4. Записать уравнение характеристик:

; (2)

5. Решить уравнение (2). Для этого:

а) разрешить уравнение (2) как квадратное уравнение относительно dy:

; (3)

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):

· (4)

в случае уравнения гиперболического типа;

· , (5)

в случае уравнения параболического типа;

· , (6)

в случае уравнения эллиптического типа.

6. Ввести новые (характеристические) переменные и :

· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т. е.

· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т. е. , в качестве берут произвольную, дважды дифференцируемую функцию , не выражающуюся через , т. е. ;

· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:

, (7)

8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:

· в случае уравнения гиперболического типа:

;

· в случае уравнения параболического типа:

;

· в случае уравнения эллиптического типа:

1.2. Пример выполнения задачи 1.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение гиперболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (9)

5. Решим уравнение (9). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy: ;

;

(10)

б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):

6. Введём характеристические переменные:

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на -100 (коэффициент при ):

Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид

где

1.3. Пример выполнения задачи 2.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты . В нашем примере они постоянны:

2. Вычислим выражение :

3. уравнение параболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (12)

5. Решим уравнение (12). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:

;

(13)

б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):

6. Введём характеристические переменные: одну из переменных вводим как и ранее

а в качестве берут произвольную, дважды дифференцируемую функцию, не выражающуюся через , пусть

;

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.

После деления на 25 (коэффициент при ):

Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид

где

1.4. Пример выполнения задачи 3.

Определить тип уравнения

(14)

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение эллиптического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (15)

5. Решим уравнение (15). Для этого:

а) разрешаем уравнение (15) как квадратное уравнение относительно dy: ; (16)

б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

(17)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на 4 (коэффициент при и ):

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид

где

1.5. Задачи для самостоятельного решения.

Определить тип уравнения и привести его к каноническому виду.

§2. Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2. 1. Необходимый теоретический материал

В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

(1)

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов

· в случае уравнения гиперболического типа:

; (11)

· в случае уравнения параболического типа:

; (12)

· в случае уравнения эллиптического типа:

. (13)

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

, (14)

где — новая неизвестная функция, — параметры, подлежащие определению. Такая замена не «испортит» канонического вида, но при этом позволит подобрать параметры так, чтобы из трех слагаемых группы младших производных в уравнении осталось только одно. Уравнения гиперболического, параболического и эллиптического типов соответственно примут вид

;

Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

(15)

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).