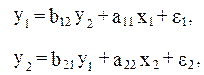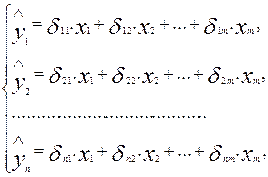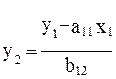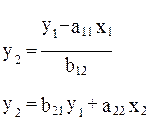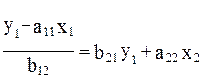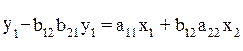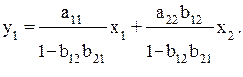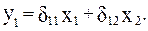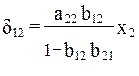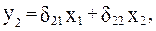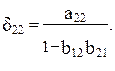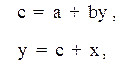Приведенная форма системы линейных уравнений

Система линейных одновременных уравнений. Структурная и приведенная формы эконометрической модели.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные обозначены в приведенной ранее системе одновременных уравнений как у. Это зависимые переменные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как x. Это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Простейшая структурная форма модели имеет вид:

где y – эндогенные переменные;

x – экзогенные переменные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Так, потребление текущего года (y_t) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (y_t-1)

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

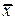
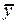
Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты b_i и a_j, (b_i – коэффициент при эндогенной переменной, a_j – коэффициент при экзогенной переменной), которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонения от уровня, т. е. под x подразумевается x- а под y — соответственно у- . Поэтому свободный член в каждом уравнении системы отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные структурных коэффициентов модели структурная коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

где 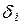— коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели ( ) через коэффициенты структурной модели (a_j и b_i). Для упрощения в модель не введены случайные переменные.

Для структурной модели вида

и (4.1)

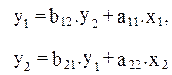
Приведенная форма модели имеет вид

и (4.2)

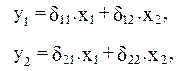
В которой y₂ из первого уравнения структурной модели можно выразить следующим образом:

Тогда система одновременных будет представлена как

Отсюда имеем равенство:

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной модели, т. е.

и

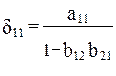
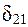
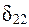
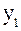
Аналогично находятся и коэффициенты приведенной формы модели второго уравнения системы ( и ) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную из второго структурного уравнения и подставим во второе.

Что соответствует уравнению приведенной формы модели:

и

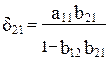
Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи еменную им турнвязаны с коэффодели второго уравнения системы ()дели в виде уравнения приведенной формы модели:

между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Так, в 1947 г., исследуя линейную зависимость потребления (c) от дохода (y), Т. Хавельмо предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:

где х – инвестиции в основной капитал и запасы экспорта и импорта;

a и b – параметры линейной зависимости c от y.

Их оценки должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии.

В этой модели две эндогенные переменные – c и y и одна экзогенная переменная x. Система приведенных приведенных уравнений составит:

Она позволяется получить значения эндогенной переменной с через переменную х. Рассчитав коэффициенты приведенной формы модели (A₀, A₁, B₀, B₁), можно перейти к коэффициентам структурной модели a и b, подставляя в первое уравнение приведенной формы выражение переменной x из второго уравнения приведенной формы модели. Приведенная форма модели хотя и значения экзогенных переменных, аналитически уступает структурной форме модели, так в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

Дата добавления: 2016-05-16 ; просмотров: 1364 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Общая теория систем линейных уравнений

Условия совместности.

Займемся изучением систем из m уравнений с n неизвестными. Систему
\begina_<1>^<1>x^<1>+a_<2>^<1>x^<2>+. +a_^<1>x^=b^<1>,\\a_<1>^<2>x^<1>+a_<2>^<2>x^<2>+. +a_^<2>x^=b^<2>,\\\cdots\\a_<1>^x^<1>+a_<2>^x^<2>+. +a_^x^=b^\end мы можем кратко записать в виде \tag <1>A\boldsymbol=\boldsymbol.
Система задается своей расширенной матрицей A^ <*>, получаемой объединением матрицы системы A и столбца свободных членов \boldsymbol .

Простое и эффективное условие, необходимое и достаточное для совместности системы (1) , дает следующая теорема, называемая теоремой Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров m \times n столбца \boldsymbol высоты m не меняет ее ранга тогда и только тогда, когда этот столбец — линейная комбинация столбцов A .

Если \mathbf\,A^ <*>= \mathbf\,A , то базисный минор A является базисным и для A^ <*>. Следовательно, \boldsymbol раскладывается по базисным столбцам A . Мы можем считать его линейной комбинацией всех столбцов A , добавив недостающие столбцы с нулевыми коэффициентами.

Обратно, если \boldsymbol раскладывается по столбцам A , то элементарными преобразованиями столбцов можно превратить A^ <*>в матрицу A_ <0>, получаемую из A приписыванием нулевого столбца. Из утверждения о том, что ранг матрицы не меняется при элементарных преобразованиях, следует \mathbf\,A_ <0>= \mathbf\,A^ <*>. С другой стороны, \mathbf\,A_ <0>= \mathbf\,A , так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда \mathbf\,A = \mathbf\,A^ <*>, как и требовалось.

Иначе это утверждение можно сформулировать так.

Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.

Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.

Транспонируем матрицу A системы (1) и рассмотрим систему из n линейных уравнений \tag <2>\begin a_<1>^<1>y_<1>+a_<1>^<2>y_<2>+. +a_<1>^y_=0,\\ a_<2>^<1>y_<1>+a_<2>^<2>y_<2>+. +a_<2>^y_=0,\\\cdots\\a_^<1>y_<1>+a_^<2>y_<2>+. +a_^y_=0\end с m неизвестными, матрицей A^и свободными членами, равными нулю. Она называется сопряженной однородной системой для системы (1) . Если \boldsymbol — столбец высоты m из неизвестных, то систему (2) можно записать как A^\boldsymbol=\boldsymbol , или лучше в виде \tag <3>\boldsymbol^A=\boldsymbol, где \boldsymbol — нулевая строка длины n .

Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению \tag <4>\boldsymbol^\boldsymbol=y_<1>b^<1>+. +y_b^=0.

1^ <\circ>. Пусть система (1) совместна, то есть существует столбец \boldsymbol высоты n , для которого A\boldsymbol=\boldsymbol . Тогда для любого столбца \boldsymbol высоты m выполнено \boldsymbol^A\boldsymbol=\boldsymbol^\boldsymbol . Если \boldsymbol — решение системы (3) , то \boldsymbol^\boldsymbol=(\boldsymbol^A)\boldsymbol=\boldsymbol\boldsymbol=0 .

2^ <\circ>. Предположим теперь, что система (1) несовместна. Тогда согласно утверждению 1 строка \begin 0&. & 0& 1 \end входит в упрощенный вид расширенной матрицы A^<*>=\begin A& |& \boldsymbol \end и, следовательно, является линейной комбинацией ее строк. Обозначим коэффициенты этой линейной комбинации y_<1>. y_ и составим из них столбец \boldsymbol . Для этого столбца \boldsymbol^\begin A& |& \boldsymbol \end=\begin 0&. & 1 \end (согласно данного утверждения). Это же равенство можно расписать как два: \boldsymbol^A=\boldsymbol и \boldsymbol^\boldsymbol=1 . Итак, нам удалось найти решение системы (3) , не удовлетворяющее условию (4) . Это заканчивает доказательство.

В качестве примера применим теорему Фредгольма к выводу условия параллельности двух различных прямых на плоскости. Их уравнения составляют систему A_<1>x+B_<1>y+C_<1>=0,\ A_<2>x+B_<2>y+C_<2>=0.
Она не имеет решений, если существуют такие числа y_<1>, y_ <2>, что y_<1>A_<1>+y_<2>A_<2>=0 , y_<1>B_<1>+y_<2>B_<2>=0 , но y_<1>C_<1>+y_<2>C_ <2>\neq 0 . Ясно, что y_ <1>и y_ <2>не равны нулю. Поэтому можно положить \lambda=-y_<2>/y_ <1>и записать полученное условие в виде: существует число \lambda такое, что A_<1>=\lambda A_ <2>, B_<1>=\lambda B_ <2>и C_ <1>\neq \lambda C_ <2>.

Нахождение решений.

В этом пункте мы будем предполагать, что дана совместная система из m линейных уравнений с n неизвестными. Ранг матрицы системы обозначим r . Поскольку ранг расширенной матрицы тоже равен r , мы можем считать базисные столбцы матрицы системы базисными столбцами расширенной матрицы. Элементарными преобразованиями строк приведем расширенную матрицу к упрощенному виду (возможность этого мы уже доказывали). Наша система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.

Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде \tag <5>\begin x^<1>=\beta^<1>-(\alpha_^<1>x^+. +\alpha_^<1>x^),\\\cdots\\x^=\beta^-(\alpha_^x^+. +\alpha_^x^).\end
Здесь \alpha_^ и \beta^ — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.

Как бы мы ни задали значения параметрических неизвестных, по формулам (5) мы найдем значения базисных так, что они вместе со значениями параметрических неизвестных образуют решение системы (1) . Легко видеть, что так мы получим все множество решений.

На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.

Приведенная система.

Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: \tag<6>A\boldsymbol=\boldsymbol. По отношению к системе (1) она называется приведенной.

Пусть \boldsymbol_ <0>— решение системы (1) . Столбец \boldsymbol также будет ее решением тогда и только тогда, когда найдется такое решение у приведенной системы (6) , что \boldsymbol=\boldsymbol_<0>+\boldsymbol .

Пусть \boldsymbol — решение системы (1) . Рассмотрим разность \boldsymbol=\boldsymbol-\boldsymbol_ <0>. Для нее A\boldsymbol=A\boldsymbol-A\boldsymbol_<0>=\boldsymbol-\boldsymbol=\boldsymbol .

Обратно, если \boldsymbol — решение системы (6) , и \boldsymbol=\boldsymbol_<0>+\boldsymbol , то A\boldsymbol=A\boldsymbol_<0>+A\boldsymbol=\boldsymbol+\boldsymbol=\boldsymbol .

Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.

Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.

Пусть столбцы матрицы A линейно независимы, то есть \mathbf\,A=n . Тогда система (6) имеет единственное решение (ранее мы это уже доказывали) и, следовательно, нетривиальных решений не имеет.

Если \boldsymbol_ <1>и \boldsymbol_ <2>— решения однородной системы, то любая их линейная комбинация — также решение этой системы.

Действительно, из A\boldsymbol_<1>=\boldsymbol и A\boldsymbol_<2>=\boldsymbol для любых \alpha и \beta следует A(\alpha \boldsymbol_<1>+\beta \boldsymbol_<2>)=\alpha A \boldsymbol_<1>+\beta A\boldsymbol_<2>=\boldsymbol .

Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.

Матрица F , состоящая из столбцов высоты n , называется фундаментальной матрицей для однородной системы с матрицей А, если:

1. AF=O ;
2. столбцы F линейно независимы;
3. ранг F максимален среди рангов матриц, удовлетворяющих условию 1).

Столбцы фундаментальной матрицы называются фундаментальной системой решений.

Если фундаментальная матрица существует, то каждый ее столбец в силу первого условия определения — решение системы. Если система не имеет нетривиальных решений, то фундаментальной матрицы нет. Это будет в том случае, когда столбцы А линейно независимы: \mathbf\,A=n .

Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.

Пусть A — матрица размеров m \times n и ранга r . Если AF=O , то \mathbf\,F \leq n-r .

Приведем матрицу A к упрощенному виду элементарными преобразованиями строк, а затем элементарными преобразованиями столбцов обратим в нулевые все небазисные столбцы. Мы получим матрицу A’=PAQ , где P и Q — произведения соответствующих элементарных матриц. Первые r строк A’ — строки единичной матрицы порядка n , а остальные — нулевые. Обозначим F’=Q^<-1>F . Тогда \mathbf\,F’ = \mathbf\,F . Используя ранее доказанное нами утверждение, легко заметить, что первые r строк матрицы A’F’ совпадают с первыми r строками F’ . Но A’F’=PAF=O и, следовательно, F’ содержит r нулевых строк. Так как всего в ней n строк, \mathbf\,F’ \leq n-r . Это равносильно доказываемому утверждению.

Покажем теперь, как может быть построена фундаментальная матрица. Согласно ранее доказанному утверждению, решение однородной системы состоит из коэффициентов равной нулю линейной комбинации столбцов матрицы системы. Мы можем получить такие линейные комбинации, основываясь на теореме о базисном миноре. Снова для удобства записи будем считать, что в матрице A первые r столбцов — базисные. Каждый из небазисных столбцов \boldsymbol_ (j=r+1. n) раскладывается по базисным: \tag <7>\boldsymbol_=\alpha_^<1>\boldsymbol_<1>+. +\alpha_^\boldsymbol_. Отсюда следует, что столбец \begin -\alpha_^<1>. -\alpha_^& 0. 0& 1& 0. 0 \end^решением. (Единица в нем стоит на j -м месте.)

Таких решений можно составить столько, сколько есть небазисных столбцов, то есть (n-r) . Убедимся в том, что эти решения линейно независимы. Для этого объединим все столбцы в одну матрицу \tag <8>\begin -\alpha_^<1>& -\alpha_^<1>&. -\alpha_^<1>,\\\cdots\\-\alpha_^& -\alpha_^&. -\alpha_^,\\1& 0&. & 0\\0& 1&. & 0\\\cdots\\0& 0&. & 1\end.
Подматрица в последних n-r строках — единичная. Поэтому ранг матрицы (8) равен числу столбцов, и столбцы линейно независимы.

Таким образом, мы получили

Если ранг матрицы однородной системы линейных уравнений r меньше числа неизвестных n , то система имеет фундаментальную матрицу из n-r столбцов.

Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.

Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.

Пусть F — фундаментальная матрица системы A\boldsymbol=\boldsymbol . Рассмотрим произвольный столбец с высоты n-r . Произведение F\boldsymbol — столбец высоты n , и из равенства AF\boldsymbol =\boldsymbol следует, что при любом с столбец F\boldsymbol — решение системы. Оказывается, имеет место

Столбец \boldsymbol — решение системы A\boldsymbol=\boldsymbol тогда и только тогда, когда существует такой столбец \boldsymbol , что \tag <9>\boldsymbol=F\boldsymbol.

Остается доказать необходимость условия. Пусть \boldsymbol — решение. Присоединив его к F , получим матрицу F^<*>=\begin F\ |\ \boldsymbol \end . Эта матрица удовлетворяет условию AF^<*>=O , так как каждый ее столбец — решение. Значит, \mathbf\,F^<*>=n-r . По теореме Кронекера-Капелли мы заключаем отсюда, что существует столбец \boldsymbol , удовлетворяющий системе F\boldsymbol=\boldsymbol .

Общее решение системы линейных уравнений.

Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.

Выражение, стоящее в правой части формулы (10) , называется общим решением системы линейных уравнений. Если \boldsymbol_<1>. \boldsymbol_ — фундаментальная система решений, а c_<1>. c_ — произвольные постоянные, то формула (10) может быть написана так: \tag <11>\boldsymbol=\boldsymbol_<0>+c_<1>\boldsymbol_<1>+. +c_\boldsymbol_.

Теорема 3 верна, в частности, и для однородных систем. Если \boldsymbol_ <0>— тривиальное решение, то (10) совпадает с (9) .

Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.

Пусть A — матрица системы из n линейных уравнений с n неизвестными. Если \det A=0 , то система либо не имеет решения, либо имеет бесконечно много решений.

Равенство \det A=0 означает, что \mathbf\,A и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.

Пример.

Рассмотрим уравнение плоскости как систему \tag<12>Ax+By+Cz+D=0 из одного уравнения. Пусть A \neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0 . Мы получим x=-D/A . Так как n=3 , r=1 , фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1 , z=0 и y=0 , z=1 . Соответствующие значения базисной неизвестной x , найденные из приведенной системы, будут -B/A и -C/A . Итак, общее решение системы (12) \tag <13>\begin x\\ y\\ z \end=\begin -D/A\\ 0\\ 0 \end+c_ <1>\begin -B/A\\ 1\\ 0 \end+c_ <2>\begin -C/A\\ 0\\ 1 \end.

Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение \begin -D/A& 0& 0 \end^состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле (10) решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже знаем, что компоненты лежащих в плоскости векторов удовлетворяют уравнению A\alpha_<1>+B\alpha_<2>+C\alpha_<3>=0 , то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула (13) — не что иное, как параметрические уравнения плоскости.

Матрицы: метод Гаусса. Вычисление матрицы методом Гаусса: примеры

Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.

Основные понятия

Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.

Вам будет интересно: Закон Максвелла. Распределение Максвелла по скоростям

Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.

Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.

Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.

Ступенчатый вид матрицы

Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l Понравилась статья? Поделись с друзьями: