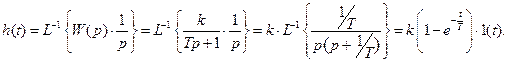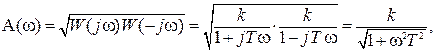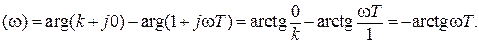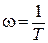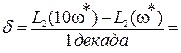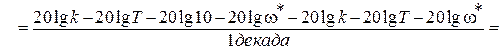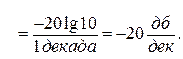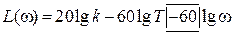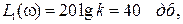Приведите примеры инерционных звеньев и их уравнение

III.1.2 Инерционное звено

Звено называется инерционным, если связь между входным х(t) и выходным z(t) сигналами звена определяется дифференциальным уравнением вида

. (III.1.2)

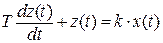
Смысл коэффициентов T и k будет прояснен позже. Такое звено называют также апериодическим, статическим, одноёмкостным, релаксационным.

Надо заметить, что этот тип звена наиболее часто встречается в практике автоматического регулирования. В качестве примеров инерционного звена можно назвать термопару, магнитный усилитель, двигатель постоянного тока с независимым возбуждением, генератор и т.д.

Если к (III.1.2) применить преобразование Лапласа при нулевых

начальных условиях, то получится

.

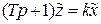
Найдем отсюда передаточную функцию звена

. (III.1.3)

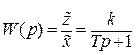
Переходная характеристика звена определиться из выражения

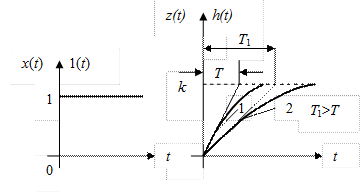
На рисунке III.6 представлены для сравнения сигналы

Рис. III.6 Единичный скачок и переходная

функция инерционного звена.

Из рисунка видно, что, сравнивая установившееся значение выходного сигнала звена k и величину входного 1(t), можно сделать вывод, что параметр k в (III.1.2) есть коэффициент усиления звена. Из этого же рис. III.6. видно, что кривая 2 характеризует более замедленную, более инертную реакцию звена на единичный скачок. Для кривой 2 параметр Т₁ (смысл которого ясен из рисунка) больше параметра Т для кривой 1. Значит, этот параметр может служить мерой инерционности звена. Обычно этот коэффициент Т называют постоянной времени звена.

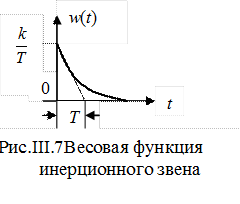
Импульсная переходная (весовая) функция звена w(t), представленная на рис. III.7, определяется следующим образом

.

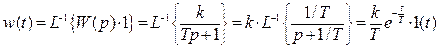
Получим частотную передаточную функцию звена W(jω), заменив в (III.1.3) р на jω

.

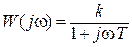
Отсюда легко определяются АЧХ A(ω) и ФЧХ φ(ω)

φ

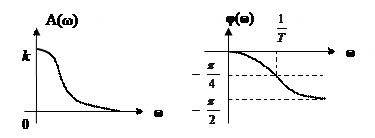
Качественный вид графиков, соответствующих вышенайденным зависимостям A(ω) и φ(ω), представлен на рис. III.8.

Рис.III.8. АЧХ и ФЧХ инерционного звена.

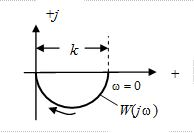
По найденным графикам A(ω) и φ(ω) на рис. III.9. построена амплитудно-фазовая характеристика инерционного звена

Рис. III. 9. АФХ инерционного звена.

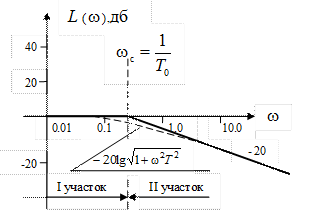
Из выражения для АЧХ звена получим соотношение для точной ЛАЧХ

. (III.1.4)

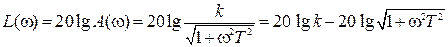
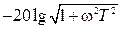
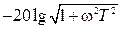
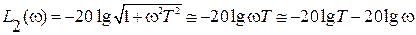
В выражении для L(ω) вычислять слагаемое для различных частот от 0 до ∞ представляет определенные неудобства. Вот если бы удалось диапазон частот 0 ≤ ω 1. Тогда асимптота второго участка может быть получена, если в выражении пренебречь первым слагаемым подкоренного выражения по сравнению со вторым

.

Поскольку при построении ЛАЧХ частоты по оси абсцисс откладываются в логарифмическом масштабе, то вторая асимптота представляет собой уравнение прямой, зависящей от частоты ω (т.е. проходящей с некоторым наклоном к оси частот). Ниже будет показано, как определять наклон таких асимптот.

Когда же сопрягаются, т.е. становятся равными, эти две асимптоты L₁(ω) и L₂(ω)? Очевидно, тогда, когда первое слагаемое подкоренного выражения точной кривой 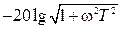становится равным второму

Отсюда частота, при которой сопрягаются обе асимптоты, или сопрягающая частота

.

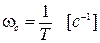
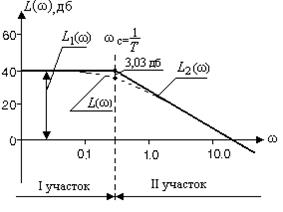
Асимптоты L₁(ω) и L₂(ω) представляют собой совокупность прямых, приблизительно заменяющих точную кривую 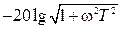(рис. III.10). На этом рисунке помимо асимптот L₁(ω) и L₂(ω) пунктиром показана и упомянутая точная кривая.

Рис. III.10. Точная ЛАЧХ

Вернемся к выражению (III.1.4) для точной ЛАЧХ звена и построим асимптоты, приблизительно ее заменяющие.

Начинать построение ЛАЧХ рекомендуется с определения сопрягающих частот. Сопрягающих частот у ЛАЧХ будет столько, сколько звено (или САР) имеет постоянных времени. В случае инерционного звена из (III.1.3) видно, что имеется лишь одна постоянная времени Т и, значит, одна сопрягающая частота

.

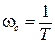
Эта сопрягающая частота делит ось частот на два участка ω ω_c. Для более сложных звеньев или САР число постоянных времени может достигать произвольного значения m, тогда число участков будет m+1.

В случае инерционного звена рассмотрим

или ω T 1. (III.1.6)

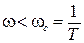
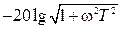
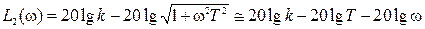
Выражение для асимптоты II участка получается аналогично предыдущему случаю, только учитывать надо условие (III.1.6) и в члене следует пренебречь первым слагаемым по сравнению со вторым

.

Как уже говорилось выше, с учетом логарифмического масштаба по оси частот данное выражение представляет собой прямую линию, имеющий некоторый наклон к оси абсцисс. Чтобы провести эту асимптоту на графике, необходимо знать ее наклон и точку, через которую проходит данная прямая. Что касается упомянутой точки, то найти ее легко, если понять, что конец предыдущей асимптоты является началом следующей. В самом деле, если взять конец первой асимптоты, т.е. ее значение при

,

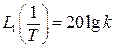
и начало второй асимптоты, т.е. ее значение при той же частоте

,

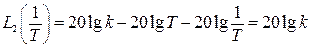
то подтверждается вышеприведенное утверждение

.

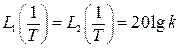
Для определения наклона асимптоты к оси абсцисс найдем для частоты ω * , относящейся ко II участку

.

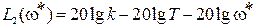
Затем увеличим частоту ω * в 10 раз (т.е. на декаду) и получим значение L₂(10 ω * )

.

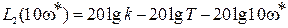
Легко понять, что если взять приращение ЛАЧХ

и отнести его к интервалу изменения частоты, то тем самым определиться наклон асимптоты к оси частот

Итак, наклон второй асимптоты L₂(ω) составляет 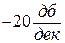, т.е. при росте частоты на 1 декаду L₂(ω) уменьшается на 20 дб.

Вообще же, чтобы не определять каждый раз подобным способом наклоны произвольной асимптоты полезно запомнить следующее правило: наклон асимптоты к оси частот определяется коэффициентом со знаком, стоящим при члене lgω в выражении для асимптоты.Например, если

,

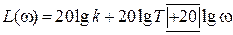
то соответствующий наклон равен 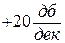, а при

этот наклон будет .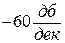

На рис. III.11 изображена ЛАЧХ инерционного звена своими асимптотами (для к = 100)

.

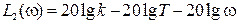
Часто ЛАЧХ звена или системы характеризуют путем обозначения наклонов ее асимптот. В данном случае эта характеристика будет выглядеть так .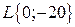

Рис. III. 11 ЛАЧХ инерционного звена.

На этом же рисунке пунктиром изображена точная ЛАЧХ L(ω) (III.1.4). Видно, что максимальная ошибка, возникающая от замены точной ЛАЧХ на асимптотическую, наблюдается на сопрягающей частоте 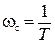и для инерционного звена приблизительно равна 3,03 дб.

Чтобы оценить влияние параметров звена k и T на его ЛАЧХ, надо понять, что изменение k приводить к изменению 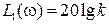. Иными словами, при изменении k первая асимптота перемещается по вертикали параллельно самой себе. Но так как конец первой асимптоты является началом второй, т.е. первая и вторая асимптоты жестко связаны, то точно такое же перемещение по вертикали будет претерпевать и вся асимптотическая ЛАЧХ.

Понятно так же, что при изменении Т меняется сопрягающая частота 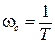. Значит, при изменении T ЛАЧХ инерционного звена будет перемещаться по горизонтали параллельно самой себе.

Дата добавления: 2016-04-14 ; просмотров: 2687 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением)

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

Для вывода уравнения инерционно-интегрирующего звена интегрирующеезвеносзамедлением обратимся к нашему любимому гидравлическому демпферу.

Мы уже рассматривали систему уравнений и динамическую модель вот в этой Математическое описание систем автоматического управления ч. 2.9 — 2.13.

Немного модифицируем исходную модель, заменив пружину на внешнее воздействие. Схема видоизменной модели приведена на рисунке 1.

Рисунок 3.8.0. Схема гидравлического демпфера.

Уравнения движения плунжера при данной схеме принимают вид:

— масса плунжера;

— ускорение плунжера;

— давление в камере гидроцелиндра;

— площадь плунжера;

— сила действующая на плунжер возмущающее воздействие;

— коэффициент трения скольжения;

— корость перемещения плунжера;

— сила трения.

Если объем камеры достаточно большой, а модуль объемной упругости маленький, то малые перемещения плунжера не меняют давление в камере. Можно перенять, что p = cost; Тогда начальное значение силы, при которой систем находится в равновесии:

А входное воздействие можно записать как:

Получим уравнение в виде:

Заменим переменные. Пусть для звена входным xt воздействием будет относительное отклонение силы от начального равновесного состояния, тогда изменив обозначение получим:

А выходным значение yt будет относительное отклонение от начального положения плунжера:

тогда для производных:

Подставляя в уравнения, получим:

Если разделить все уравнение на Fполучим уравнение инерционно интегрирующего звена:

Мы опять получили размерность времени для коэффициентов уравнения динамики.

Если разделить обе части уравнения на T₁ 3.8.1, можно получить вторую форму уравнения для инерционно-интегрирующего звена:

Во втором случае размерность коэффициента

Используя преобразования по Лапласу, получим две формы уравнения в изображениях:

Передаточная функция в двух вариантах:

где -безразмерный кофээфицента, а

АФЧХ:

Анализ формул и при разных значения показывает что:

Рисунок 3.8.1 АФЧХ инерционно-интегрирующего звена (если k – безразмерный коэффициент)

Для воторого варианта передаточной функции:

Анализ формул и при разных значения показывает что:

Рисунок 3.8.2 АФЧХ инерционно-интегрирующего звена (если k имеет размерность 1/с)

Амплитуда модуль:

Сдвиг фазы:

Логарифмическая амплитудная характеристика ЛАХ:

Построим соответствующие графики:

Рисунок 3.8.3 АЧХ и ФЧХ инерционно-интегрирующего звена Рисунок 3.8.4 ЛАХ и ЛФЧХ инерционно-интегрирующего звена

Переходная функция находится, с использованием передаточной функции и функции единичесного сутпенчатого воздействия 1t, в изображениях единичное ступенчатое воздействие —

Для нахождения оригинала по изображению воспользуемся формулой Хэвисайда, для изображений имеющих вид:

, где D₁s и D₀s – полиномы по степеням «s», оригинал принимает вид:

где s_j – полюса изображения, т.е. те значения «s» при которых полином D₀s обращается в ноль; k_j – кратность j – го полюса.

Полиномы функции функции

Полюса полинома

Рисунок 3.8.5 Переходная функция инерционно-интегрирующего звена

Весовая функция получается дифференцированием по времени переходной:

Примерами инерционно-интегрирующих звеньев являются:

Интегрирующий привод (например, электродвигатель с редуктором с учетом механической инерционности якоря двигателя и зубчатых колес редуктора), где входное воздействие – напряжение в обмотке возбуждения, выходное – угол поворота выходного вала редуктора)

Гидравлический демпфер, если учитывать инерционность поршня и сопротивление трения (F(t) – входное воздействие, y(t) – выходной параметр).

Пример

Мы уже обращали внимание, что абсолютно разные физические системы с помощью волшебства «Теории Автоматического Управления» превращаются в абсолютно одинаковые математические модели. Например, в лекции «Апериодическое звено 1-го порядка» камера смешения реактора (теплогидравлические уравнения) и электрическая цепь (уравнения электротехники) описываются одинаковыми передаточными функциями. И при моделировании выдают одинаковые графики АФЧХ и годографов!

В этой лекции у нас обратное волшебство: одна и та же физическая система может быть представлена разными передаточными функциями. Попробуем посмотреть на это волшебство на примере сравнения разных математических моделей для одной и той же системы – гидравлического демпфера. Сравнивать будем отклик на ступенчатое воздействие.

В статье «Математическое описание систем автоматического управления ч. 2.9 — 2.13» мы уже разбирали способы создания математической модели такого гидравлического демпфера. Для удобства построения графика изменим направление оси х так, чтобы положительное направление совпадало с направление действия силы. См. схему на рисунке 3.8.10:

Рисунок 3.8.10. Схема модели гидравлического демпфера

Тогда уравнение движения плунжера примет следующий вид:

В начале лекции мы принимаем допущение, что объем камеры большой, а величина перемещения плунжера и модуль упругости среды малые настолько, что перемещение не вызывает изменения давления. И получаем уравнения для инерционно-интегрирующего звена. Составим модель в виде структурной схемы из типовых блоков:

Рисунок 3.8.11. Структурная схема модели плунжера при p = const

В качестве параметров возьмем основные технические характеристики, которые были использованы при решении подобной задачи ранее, и запишем их в глобальном скрипте модели:

Рисунок 3.8.12. Параметры модели.

В начальный момент входное воздействие уравновешивает давление в камере, на первой секунде происходит увеличение на 10Н. Параметры блока приведены на рисунке 5.

Рисунок 3.8.13. Параметры ступенчатого воздействия

Результат такого воздействия вызывает перемещение плунжера в полном соответствии с теоретическим решением в лекции. На рисунке 3.8.14 представлен график перемещения плунжера в течение 3 секунд, а также увеличенный участок сразу после ступенчатого изменения воздействия.

Рисунок 3.8.14 Перемещение плунжера.

Модель в виде структурной схемы, повторяющей уравнения движения, можно представить в виде одного блока «Инерционно-интегрирующее звено». Как было показано в начале, параметры блока будут следующими:

В формуле коэффициента усиления присутствует начальное положение x₀, которое необходимо для пересчета из относительной величины перемещения в абсолютную. Но поскольку сам пересчет заключается в умножении на x_{0 ,} то ее можно сократить, Таким образом, мы получим сразу перемещение в абсолютных единицах [м], а параметры блока инерционно-интегрирующего звена будут такими, как показано на рисунке 3.8.15

Рисунок 3.8.15. Параметры модели в виде одного блока.

Для использования данного блока в модели необходимо размерные параметры силы перевести в безрамные с помощью блока линейное преобразование. Тогда общая модель будет выглядеть так, как показано на рисунке 3.8.16:

3.8.16. Сравнение модели в виде блока и схемы

Результаты моделирования показывают полное совпадение модели в виде одного блока и модели в виде структурной схемы см. рис. 3.8.17

Рисунок 3.8.17 Сравнение схемы и блока.

Сравним модель с постоянным давлением в камере с моделью, где учитывается сжимаемость жидкости и изменение объема при перемещении плунжера, но расход со стороны дросселя Q равен 0.

В общем случае производная давления в камере будет описываться следующим уравнением:

Где: Q – расход в камере (у нас он равен 0), V — объем камеры, Ap – площадь плунжера, x’- скорость перемещения, E — объемный модуль упругости. Поскольку мы изменили направление х, то положительная величина скорости будет увеличивать давление в камере (см. рис. 3.8.10).

Создадим вторую модель с учетом сжимания в среды камере демпфера (см. рис. 3.8.18)

Рисунок 3.8.18 Модель плунжера с камерой

Сравнение расчёта двух моделей показывает, что учет сжимаемости жидкости в камере сразу приводит к кардинально другим результатам: вместо линейного роста перемещения мы получаем колебательный процесс и новое положение равновесия, жидкость в камере с учетом сжимаемости ведет себя как пружина, однако на масштабированном графике видно, что в начальный момент времени графики двух моделей достаточно хорошо совпадают (см. рис. 3.8.19):

Рисунок 3.8.19 Сравнение моделей с камерой и без камеры (среда — жидкость)

Таким образом упрощенная модель может достаточно точно описывать поведение демпфера при малых перемещениях и нагрузках.

В примере выше в качестве среды используется жидкость с модулем объемной упругости E = 13e8. Если вместо жидкости в демпфере будет использоваться воздух с модулем упругости E = 1.42e5, при тех же воздействиях мы увидим переходной процесс, приведенный на рисунке 3.8.20, где совпадения процессов идут в более широком диапазоне перемещения.

Рисунок 3.8.20 Сравнение моделей с камерой и без камеры (среда – воздух).

Как мы видим, принятое упрощение модели работает только в ограниченном диапазоне перемещения. Как только перемещения плунжера становятся значительными, давление в камере начинает изменяться, и принятые допущения уже не работают. Еще раз усложним модель, добавив в модель дроссель, который соединяет камеру демпфера с источником постоянного давления.

Такая модель будет более точно отображать гидравлическую систему, в которой есть источник давления (например, магистраль) и исполнительные механизмы (гидроцилиндры).

Расход через дроссель определяется по формуле:

Q – расход через дроссель, μ — коэффициент расхода, f – площадь сечения дросселя, p_n – давление в линии нагнетания, p – давление в камере.

Значения для этих параметров возьмем из предыдущего примера и добавим в общий скрипт проекта (см. ниже). Закомментированные строки позволяют менять среду в модели (воздух или гидравлическая жидкость).

Рисунок 3.8.21 Модель с учетом дросселя.

Графики перемещения для всех трех моделей в случае среды гидравлической жидкости приведены на рисунке 3.8.22 Видно, что добавление дросселя и объема с постоянным давлением делает отклик системы более похожим на отклик одного звена (отличается только угол наклона, который соотвесвует установившемуся давление в камере).

Рисунок 3.8.22 Перемещения плунжера для разных вариантов модели (среда — жидкость).

Увеличенный график показывает, что при малых перемещениях, в начале процесса все три модели дают очень близкий результат.

Если заменить в модели жидкость на воздух (изменить модуль объемной упругости и плотность среды), то все 3 модели дают очень близкий результат в большем диапазоне перемещения плунжера. (см. рис. 3.8.23). Увеличение показывает, что все три модели ведут себя практически аналогично инерционно-интегрирующему звену.

Рисунок 3.8.23 Перемещения плунжера для разных вариантов модели (среда — воздух).

Выводы.

Приведенные примеры показывают, что при малых перемещениях плунжера демпфера вполне можно обходиться одним расчетным блоком вместо полной модели. Например, если мы исследуем вибрации с малой амплитудой. Однако, всегда нужно помнить о границах применимости принятых допущений. В рассмотренном примере при замене среды жидкости на газ упрощенная модель из одного блока работает практически идентично полной модели из трех дифференциальных уравнений и одного алгебраического.

Как показывет разобранный пример, одна и та же физическая система может моделироваться различными моделями и различными передаточными функциями в зависимости от параметров моделируемого процесса.

Апериодическое (инерционное, статическое) звено. Передаточная функция и уравнения

Дифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде:

Где: k – коэффициент передачи, Т₀ – постоянная времени.

Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции.

Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена).

Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Х_вых(р) и Х_вх(р) функций вещественных переменных Х_вых(τ) и Х_вх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа:

Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены:

Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена.

Оригинал дифференциального уравнения апериодического звена имеет следующий вид:

Операторная форма записи (изображения) уравнения апериодического звена:

Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ).

Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом:

Из полученного выражения достаточно легко выделить отношение Х_вых(р) / Х_вх(р), которое называется передаточной функцией и для апериодического звена имеет вид:

У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ).

На практике чаще всего используется АФЧХ или АФХ.

Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент).

Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α:

После использования формулы Эйлера:

Где |W| — длина вектора или вектор по модулю, i – мнимое число:

Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний.

Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид:

Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования:

Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k.

На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т₀ в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т₀ и k в передаточной функции звена.

Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак).

В бак поступает определенное количество воды с расходом Q₁. В то же время из бака вытекает вода с расходом Q₂. Регулируемый параметр в этой системе Х_вых – уровень воды в баке H.

При подаче единичного скачка Q₁ (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q₂. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k.

В литературе объекты с передаточной функцией апериодического звена называют статическими.