Привести к каноническому виду уравнение линии is

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $\sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=\pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

Приведение уравнений линий и поверхностей второго порядка к каноническому виду

Страницы работы

Содержание работы

§. 5. Приведение уравнений линий и поверхностей

второго порядка к каноническому виду

Известно, что для любой квадратичной формы на конечном действительном евклидовом пространстве в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид. Используя этот факт, любую линию или поверхность второго порядка можно привести к каноническому виду по следующему плану.

1. Для квадратичной части уравнения (т. е. квадратичной формы) находим канонический вид и ортогональное преобразование переменных, приводящее квадратичную форму к этому каноническому виду.

2. Подставляем выражение старых переменных через новые в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, в котором коэффициенты при квадратах совпадают с собственными значениями ее матрицы, свободный член не меняется, линейная часть преобразуется непосредственно.

3. Получили уравнение, не содержащее произведений переменных. С помощью преобразования параллельного переноса избавляемся от лишних слагаемых первых степеней и тем самым окончательно приводим уравнение к каноническому виду.

Если линия или поверхность второго порядка имеет центр симметрии, то решение задачи можно существенно упростить, поменяв местами 1-й и третий пункты, а второй тогда совсем исчезает.

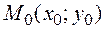
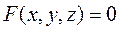
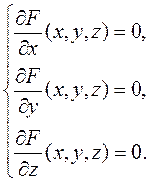
Для того чтобы точка была центром симметрии поверхности второго порядка , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений

(5. 3)

Если с помощью параллельного переноса поместить начало координат в центр симметрии поверхности второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле

. (5.4)

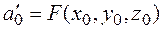
Аналогичные утверждения справедливы и для линий второго порядка (подробно обоснование см., например, в []).

Пример 1. Определить вид линии второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту линию, если ее уравнение имеет вид

. (5.5)

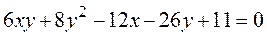
►В первую очередь проверим, имеет ли эта линия центр симметрии. Составляем систему линейных уравнений (5.3)

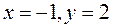
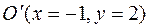
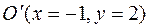
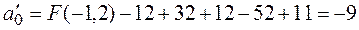
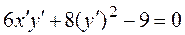
из которой находим: . Поместим с помощью параллельного переноса начало координат в точку (если в задаче используются несколько систем координат, то обязательно надо указывать, в какой именно из них вы даете координаты точки). По формуле (5.4) (подставляем координаты в левую часть (5.5)) находим . После преобразования параллельного переноса уравнение линии примет вид .

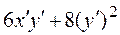
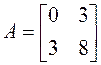
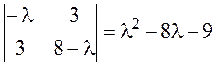
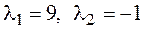
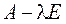
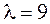
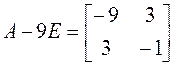
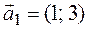
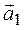
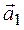
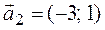
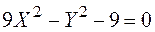
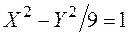
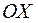
Теперь приведем к каноническому виду квадратичную часть уравнения (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:

, , .

Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей при : , . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора и в одной из них поменяв знак. Итак, . Применим ортогональное преобразование, в результате которого оси новой системы координат будут направлены по собственным векторам. После этого уравнение примет вид (коэффициенты при квадратах совпадают с найденными собственными значениями) , или , которое задает гиперболу с полуосями 1 и 3 и осью в качестве действительной.

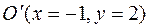
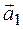
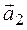
Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. Намечаем новое начало координат – точку . От этой точки откладываем собственные векторы и , которые задают направление новых осей. В полученной системе координат рисуем полученную гиперболу (рис.5.1). ◄

Замечания. 1. При таком способе решения нет необходимости выписывать ни преобразование параллельного переноса, ни ортогональное преобразование, т. к. мы и без непосредственной подстановки их в уравнение знаем, как оно преобразуется. Нет необходимости даже собственные векторы нормировать: ортогональное преобразование не нужно, а векторы с целочисленными координатами легче рисовать. Именно поэтому задачу приведения линии второго порядка к каноническому виду в том случае, когда эта линия имеет центр симметрии, сложной не назовешь.