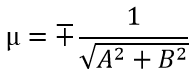Привести к нормальному виду уравнение прямой онлайн

Нормальное уравнение прямой

Как привести уравнение прямой к нормальному виду

Для того, чтобы найти нормальное уравнение прямой, заданной уравнением Ax+By+C=0, необходимо разделить данное уравнение на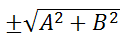

при этом знак «минус» берётся, когда C>0, а знак «плюс» берётся, когда C x cosα + y sinα − p = 0

Это и есть нормальное уравнение прямой

То же самое получим, если обе части уравнения Ах + By + С = 0 умножим на число

x cosα + y sinα − p = 0

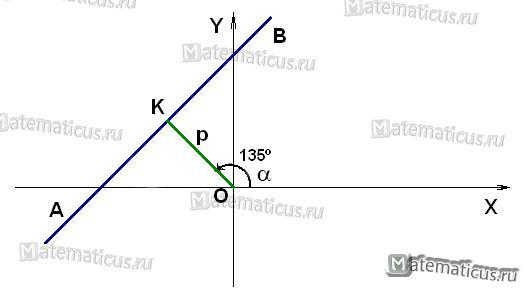
Графически это можно представить следующем образом

Прямая AB с полярным расстоянием p (длина перпендикуляра, опущенного на прямую из начала координат OK) и полярным углом α (угол измеренный в положительном направлении между положительным направлением оси Ox и направлением этого перпендикуляра) представляется уравнением:

x cosα + y sinα − p = 0

Если p=0, то прямая проходит через начало координат, а угол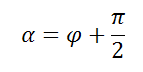

задаёт угол наклона прямой.

Пример 1
Привести уравнение 3x-4y+5=0 к нормальному виду. Здесь A=3, B=-4, C=5>0. Поэтому делим на
получаем

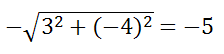
Это уравнение вида

x cosα + y sinα − p = 0

p=1, $\cos \alpha = — \frac<3><5>$, $\sin \alpha = \frac<4><5>$

Пусть прямая AB стоит от начала оси координат на расстоянии OK=$\sqrt 2 $ и пусть луч OK составляет с лучом OX угол равный α=135 0

тогда нормальное уравнение прямой AB будет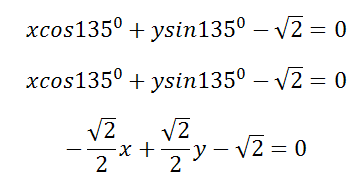

Если умножить полученное уравнение на $-\sqrt 2 $, получим уравнение прямой AB в виде

x-y+2 = 0 , но это уравнение не является нормальным уравнением прямой.

Привести к нормальному виду уравнение прямой онлайн

Уравнение прямой x + 3y — 4 = 0 привести к нормальному виду.

Нормирующий множитель определяется по формуле

Здесь A = 1; B = 3. Перед корнем надо выбрать знак, противоположный знаку свободного члена в заданном уравнении, т. е. знак плюс. Тогда нормирующий множитель

после умножения обеих частей уравнения на N уравнение примет вид

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач

В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.

Нормальное уравнение прямой – описание и пример

Рассмотрим выведение нормального уравнения.

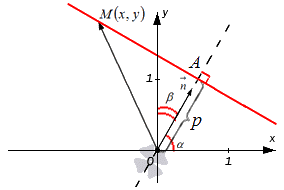
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.

Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .

O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .

Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p

Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y

Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.

Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.

Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.

Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .

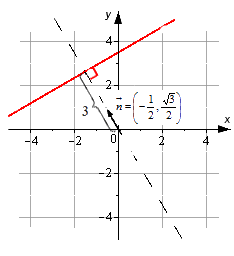
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .

Приведение общего уравнения прямой к нормальному виду

Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.

Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.

Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.

Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.

Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:

1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5

Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .

Нормальное уравнение по заданной прямой найдено.

Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .