Привести уравнение кривой к каноническому виду ортогональным преобразованием

Приведение кривой второго порядка к каноническому виду

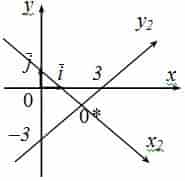
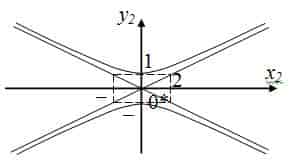
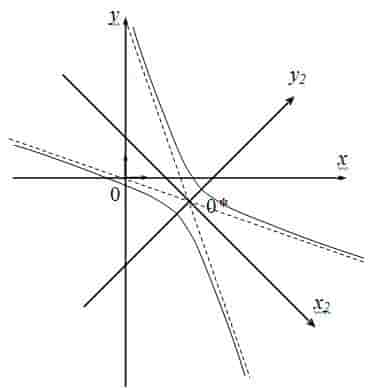
Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Канонический вид ортогонального преобразования евклидова пространства

Рассмотрим инвариантные подпространства ортогонального преобразования евклидова пространства. По теореме 9.4 линейное преобразование вещественного пространства имеет одномерное или двумерное инвариантное подпространство. Выясним геометрический смысл сужения ортогонального преобразования на инвариантное подпространство.

2. Пусть [math]L[/math] — двумерное инвариантное подпространство с ортонормированным базисом [math]\boldsymbol_1, \boldsymbol_2[/math] . Запишем для матрицы [math]A=\begin a&b\\ c&d \end[/math] ортогонального преобразования [math]\mathcal\colon L\to L[/math] равенство [math]A^T=A^<-1>:[/math]

По свойству 6 для собственного преобразования [math]\det=1[/math] , поэтому [math]d=a,

\lambda_2=-1)[/math] , так как

Поэтому несобственное ортогональное преобразование имеет два одномерных инвариантных подпространства (см. пункт 1).

Теорема (9.9) о каноническом виде ортогонального преобразования

На главной диагонали матрицы стоят либо числа 1 или (–1), либо блоки вида [math]R_<\varphi>= \begin\cos\varphi&\sin\varphi\\ -\sin\varphi&\cos\varphi \end[/math] , а остальные элементы матрицы равны нулю.

Базис [math](\boldsymbol)=(\boldsymbol_1,\ldots,\boldsymbol_n)[/math] , в котором матрица преобразования имеет вид (9.20), называется каноническим. Заметим, что канонический базис определяется неоднозначно.

Приведение ортогонального преобразования к каноническому виду

Задача приведения ортогонального преобразования к каноническому виду формулируется следующим образом: требуется найти базис (канонический), в котором матрица ортогонального преобразования имеет канонический вид (9.20). Для приведения ортогонального преобразования к каноническому виду нужно выполнить следующие действия.

Нахождение канонического вида ортогонального преобразования ( первый этап ).

1. Выбрать базис [math]\boldsymbol_1,\ldots, \boldsymbol_n[/math] евклидова пространства [math]\mathbb[/math] и найти матрицу [math]A[/math] преобразования в этом базисе.

2. Составить характеристическое уравнение [math]\det(A-\lambda E)=0[/math] и найти различные его корни [math]\lambda_1,\ldots, \lambda_k[/math] (а также их алгебраические кратности).

3. Записать блочно-диагональную матрицу (9.20) канонического вида ортогонального преобразования:

— каждый действительный корень [math]\lambda_1[/math] кратности [math]n_1[/math] поместить на главной диагонали [math]n_1[/math] раз;

— для каждой пары [math]\lambda=\alpha\pm\beta i[/math] комплексных сопряженных корней кратности [math]m[/math] записать [math]m[/math] блоков вида [math]R_<\varphi>= \begin \alpha&\beta\\ -\beta&\alpha \end[/math] (см. доказательство свойства 8 ортогональных преобразований).

Нахождение канонического базиса ( второй этап ).

4. Для действительного корня [math]\lambda_1[/math] кратности [math]n_1[/math] найти фундаментальную систему [math]x_1,\ldots,x_[/math] решений однородной системы [math](A-\lambda_1E)x=o[/math] . Линейно независимую систему [math]\boldsymbol_1,\ldots, \boldsymbol_[/math] векторов (пространства [math]\mathbb^n[/math] ) ортогонализировать и нормировать. Получим векторы [math]\boldsymbol_1,\ldots, \boldsymbol_[/math] .

5. Для пары [math]\lambda=\alpha\pm\beta i[/math] комплексных сопряженных корней кратности [math]m[/math] найти фундаментальную систему [math]z_1,\ldots,z_[/math] решений однородной системы [math](A+(\alpha+\beta i)E)z=o[/math] . Выделяя действительные [math]x_j=\operatornamez_j[/math] и мнимые части [math]y_j=\operatornamez_j,[/math] [math]j=1,\ldots,m[/math] , комплексных столбцов [math]z_1,\ldots,z_[/math] , получить [math]m[/math] пар ортогональных векторов [math]\boldsymbol_1,\boldsymbol_1; \boldsymbol_2, \boldsymbol_2;\ldots; \boldsymbol_m,\boldsymbol_m[/math] (пространства [math]\mathbb^n[/math] ). Эту систему векторов ортогонализировать и нормировать. Получим [math]2m[/math] векторов [math]\boldsymbol_1,\ldots,\boldsymbol_<2m>[/math] .

6. Выполнить пункт 4 или пункт 5 для всех различных корней характеристического уравнения. Получаемые в результате группы столбцов последовательно записать в матрицу [math]S[/math] перехода от базиса [math]\boldsymbol_1,\ldots,\boldsymbol_n[/math] к искомому каноническому базису [math]\boldsymbol_1,\ldots, \boldsymbol_n \colon\,(\boldsymbol)= (\boldsymbol)S[/math] . Матрица [math]S^<-1>AS[/math] преобразования [math]\mathcal[/math] будет иметь канонический вид (9.20), полученный в пункте 3.

1. Собственные векторы ортогональной матрицы, принадлежащие различным собственным значениям, ортогональны.

2. Из пункта 1 следует, что для получения ортонормированного базиса достаточно ортонормировать отдельно каждую группу векторов, получаемых в пункте 4 или пункте 5 алгоритма, причем по свойству 8 столбцы [math]x_j,y_j[/math] в пункте 5 будут ортогональными.

3. Матрицу вида (9.20) можно представить в виде произведения матриц, каждая из которых есть либо матрица [math]\operatorname(1,\ldots,1,-1,1,\ldots,1)[/math] простого отражения относительно гиперплоскости, либо матрица math]\operatorname(1,\ldots,1, R_<\varphi>,1,\ldots,1)[/math] простого вращения двумерной плоскости. Поэтому любое ортогональное преобразование можно представить в виде композиции простых отражений и простых вращений.

Решение. Первый этап. Нахождение канонического вида преобразования.

1. Выбираем базис [math]\boldsymbol_1, \boldsymbol_2, \boldsymbol_3[/math] , в котором задана матрица преобразования.

2. Составляем характеристическое уравнение

Уравнение имеет три простых (кратности 1) корня: один действительный [math]\lambda_1=1[/math] и пару комплексных сопряженных [math]\lambda_<2,3>= \frac<1><2>\pm\frac<\sqrt<3>><2>\,i,

3. Записываем искомый канонический вид (9.20), указывая на главной диагонали действительный корень [math]\lambda_1=1[/math] и блок [math]R_<\varphi>= \begin1/2&\sqrt<3>/2\\ -\sqrt<3>/2&1/2 \end\!,

Второй этап. Нахождение канонического базиса. Найдем матрицу [math]S[/math] перехода от данного базиса [math]\boldsymbol_1,\boldsymbol_2,\boldsymbol_3[/math] к каноническому [math]\boldsymbol_1, \boldsymbol_2, \boldsymbol_3[/math] .

4. Для действительного корня [math]\lambda_1=1[/math] кратности 1 находим фундаментальную систему решений однородной системы [math](A-\lambda_1E)x=o[/math] . Приводим матрицу системы к упрощенному виду:

Следовательно, фундаментальная система содержит одно решение [math]x=\begin 1&1&1 \end^T[/math] . Нормируя это решение (поделив координаты на норму [math]|x|= \sqrt<1^2+1^2+1^2>=\sqrt<3>[/math] ), получаем столбец [math]s_1=\begin \dfrac<\sqrt<3>><3>& \dfrac<\sqrt<3>><3>& \dfrac<\sqrt<3>><3>\end^T[/math] .

5. Для пары комплексных сопряженных корней [math]\lambda_<2,3>= \frac<1><2>\pm \frac<\sqrt<3>><2>\,i[/math] находим фундаментальную систему решений однородной системы [math](A-\lambda_2E)z=o[/math] . Приводим матрицу системы к упрощенному виду

Следовательно, фундаментальная система содержит одно решение. Полагая [math]z_3=1[/math] , получаем решение:

Выделяем действительную и мнимую части:

Нормируя столбцы, поделив координаты вектора [math]\boldsymbol[/math] на его длину

6. Записываем полученные в пункт 4, 5 столбцы [math]s_1,\,s_2,\,s_3[/math] в искомую матрицу перехода

Примеры решений. Квадратичные формы

Решения задач: квадратичные формы

Задача 1. Дано уравнение кривой второго порядка. Найти собственные значения и собственные векторы матрицы соответствующей квадратичной формы и использовать их для приведения уравнения кривой к каноническому виду.

Задача 2. Линейным преобразованием координат привести уравнение кривой второго порядка к каноническому виду и определить тип кривой.

Задача 3. Привести квадратичную форму к каноническому виду: а) методом Якоби, б) методом Лагранжа. Найти канонический базис и матрицу перехода к каноническому базису.

Задача 4. Привести квадратичную форму к каноническому виду с помощью ортогонального преобразования. Найти это преобразование, канонический базис, матрицу перехода к каноническому базису, убедиться, что в этом базисе матрица квадратичной формы является диагональной.

Задача 5. Используя теорию квадратичных форм, исследовать кривую второго порядка заданную общим уравнением и построить ее.

Задача 6. Найти линейное преобразование неизвестных, приводящее квадратичные формы, заданные своими матрицами, к каноническому виду. Выяснить, является ли квадратичная форма знакоопределенной.

$$ \begin 2 & -1 & 0\\ -1 & 2 & -1\\ 0 & -1 & 1\\ \end $$