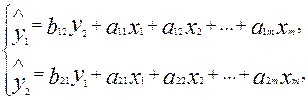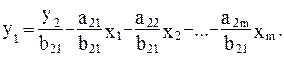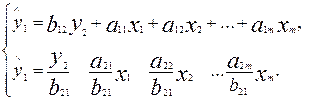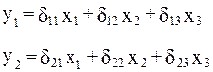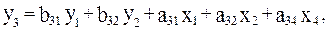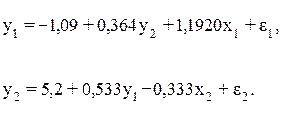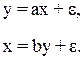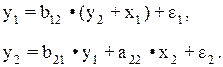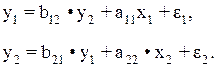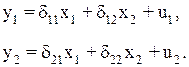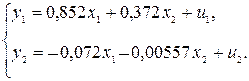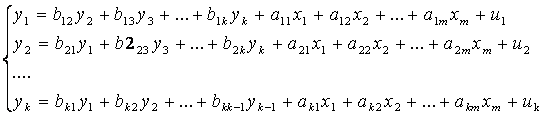Проблема идентификации параметров структурных уравнений

Проблемы идентификации

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Рассмотрим проблему идентификации для случая с двумя эндогенными переменными. Пусть структурная модель имеет вид:

Где y₁ и y₂ – совместные зависимые.

Из второго уравнения можно выразить y₁ следующей формулой:

Тогда в системе имеем два уравнения для эндогенной переменной y₁ с одним и тем же набором экзогенных переменных, но с разными коэффициентами при них:

Наличие двух вариантов для лучить значения эндогеннной авит: е от параметров обычной линейной регрессии.

расчета структурных коэффициентов одной и той же модели связано с неполной ее идентификацией. Структурная модель в полном виде, состоящая в каждом уравнении системы из n эндогенных переменных, содержит n(n-1+m) параметров. Так, при n=2 и m=3 полный вид структурной модели составит:

(4.3)

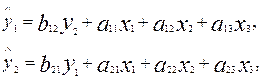
Как видим, модель содержит восемь структурных коэффициентов, что соответствует выражению n.(n-1+m).

Приведенная форма модели в полном виде содержит nm параметров. Для нашего примера это означает наличие шести коэффициентов приведенной формы модели. В этом можно убедиться, обратившись к приведенной форме модели, которая будет иметь вид:

Действительно, она включает в себя шесть коэффициентов .

На основе шести коэффициентов приведенной формы модели требуется определить восемь структурных коэффициентов рассматриваемой структурной модели, что , естественно, не может привести к единственности решения. В полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно n*(n-1+m) параметров структурной модели не могут быть однозначно определены из nm параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшиться число структурных коэффициентов модели. Так, если предположить, что в нашей модели a₁₃=0 и a₂₁=0 , то структурная модель примет вид:

(4.4)

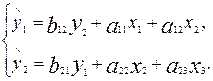
В такой модели число структурных коэффициентов не превышает число коэффициентов приведенной модели, которое равно 6. Уменьшение числа структурных коэффициентов модели

Возможно и другим путем : например, путем приравания некоторых к друг другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. На структурные коэффициенты могут накладываться, например, ограничения вида .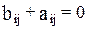

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель идентифицируемые, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Рассмотренная выше структурная модель (4.4) с двумя эндогенными и тремя экзогенными ( предопределенными) переменными, содержащая шесть структурных коэффициентов, представляет собой идентифицируемую модель.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценэмы модели. ли равно числу мы модели, т. ены через коэффициенты приведенной формы модели. Структурная модель в полном виде (4.1), содержащая n эндогенных и m предопределенных переменных в каждом уравнении системы, всегда неидентифицируема.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этом модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Так, если в структурной модели полного вида (4.1) предположить нулевые значения не только коэффициентов a₁₃ и a₂₁ (кА в модели (4.2)), но и a₂₂=0, то система уравнений станет сверхидентифицируемой:

(4.5)

В ней пять структурных коэффициентов не могут быть однозначно определены из шести коэффициентов не могут быть однозначно определены из шести коэффициентов приведенной формы модели. Сверхидентифируемая модель в отличие от не идентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемой. Сверхитифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в j-м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержаться в системе, но не входят в данное уравнение, — через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

D+1=H — уравнение идентифицируемо;

D+1 H — уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновременных уравнений:

(4.6)

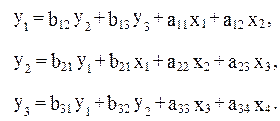
Первое уравнение точно идентифицируемо, ибо в нем присутствуют три эндогенные переменные- y₁, y₂, y₃ т.е. H=3, и две экзогенные переменные-x₁ и x₂, число отсутствующих экзогенных переменных равно двум –x₃ и x₄, D=2. тогда имеем равенство: D+1=H, т. е. 2+1=3, что означает наличие идентифицируемого уравнения.

Во втором уравнении системы H=2 (y₁ и y₂) и D=1 (x₄). Равенство D+1=H, т. е. 1+1=2. уравнение идентифицируемо.

В третьем уравнении системы H=3 (y₁, y₂, y₃), a D=2 (x₁ и x₂). Следовательно, по счетному правилу D+1=H, и это уравнение идентифицируемо. Таким образом, система (4.6) в целом идентифицируемо. Таким образом, система (4.6) в целом идентифицируема.

Предположим, что в рассматриваемой модели a₂₁=0 и a₃₃=0. Тогда система примет вид:

(4.7)

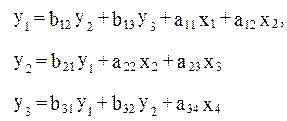
Первое уравнение этой системы не изменилось. Система по прежнему содержит три эндогенные и две экзогенные переменные, поэтому для него D=2 при H=3, и оно, как и в предыдущей системе, идентифицируемым оказывается и третье уравнение системы, где H=3 (y₁, y₂, y₃) и D=3 (x₁, x_2,x₃), т.е. счетное правило составляет неравенство: 3+1>3менные, де следующего счетного равила:

ющих в данном уравнении, но присут или D+1>H.

Модель в целом является сверхидентифицируемой.

Предположим, что последнее уравнение системы (4.7) с тремя эндогенными переменными имеет вид:

т. е. в отличие от предыдущего уравнения в него включены еще две экзогенные переменные, участвующие в системе, -x₁ и x₂. в этом случае уравнение становится неидентифицируемо, ибо при H=3, D=1 (отсутствует только x₃) и D+1 2 для каждого уравнения в отчетности. В рассматриваемом примере хороших результатов достичь не удалось: ввиду малого числа наблюдений значения F-критерия Фишера несущественны (при уровне значимости 0,005 F-табличное значение равно 19, а фактическое F=7 для первого уравнения).

Если к каждому уравнению структурной формой модели применить традиционный МНК, то результаты будут резко отличаться:

Как видим, не совпадают даже знаки коэффициентов при переменных: в первом уравнении структурной формы коэффициенты меньше нуля, а в уравнении регрессии больше нуля; во втором уравнении обратное воздействие у₁ на у₂ в структурной модели сменяется на прямое в уравнении регресс, а с фактором х₂ наоборот.

Различия между коэффициентами регрессии и структурными коэффициентами модели численно могут быть и не менее существенными. Так, например, Г. Тинтнер, рассматривая статическую модель Кейнса для австрийской экономики за 1948-1956 гг., получил функцию потребления классическим МНК в виде С = 0,782у + 71,6, а используя КМНК,

С = 0,7812у + 73,212.

При сравнении результатов, полученных традиционным МНК и с помощью КМНК, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов. Как показал Т. Хаавельмо, рассматривая две взаимосвязанные регрессии:

коэффициент регрессии отличается от структурного коэффициента и совпадает с ним только в одном частном случае, когда переменная у не содержит ошибок (т.е. e₁ = 0), а ошибки переменной х имеет дисперсию, равную единице.

Кроме того, при интерпретации коэффициентов множественной регрессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии 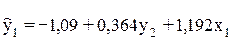показывает, что с ростом х₁ на единицу у₁ возрастает в среднем на 1,192 ед. при неизменном уровне значения у₂. Между тем в соответствии с системой одновременных уравнений переменная у₂ не может быть неизменной, ибо она в свою очередь зависит от у₁.

Нарушение предпосылки независимости факторов друг от друга при использовании традиционного МНК в системе одновременных уравнений приводит к несостоятельности оценок структурных коэффициентов; в ряде случаев они оказываются экономически бессмысленными. Опасность таких результатов возрастает при увеличении числа эндогенных переменных в правой части системы, ибо становится невозможным расщепить совместное влияние эндогенных переменных и видеть изолированные меры их воздействия в соответствии с предпосылками традиционного МНК.

Компьютерная программа применения МНК предполагает, что система уравнений содержит в правой части в каждом уравнений как эндогенные, так и экзогенные переменные. Так в п. 4.3. рассматривалась модель экономики страны с четырьмя эндогенными и двумя экзогенными переменными, в которой в первом уравнении системы не содержалось не одной экзогенной переменной. Для такой модели непосредственное получение структурных коэффициентов невозможно. В этом случае сначала определяется система приведенной формы модели, решаемая обычным МНК, а затем путем алгебраических преобразований переходят к коэффициентам структурной модели.

Двухшаговый метод наименьших квадратов (ДМНК)

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является Двухшаговый метод наименьших квадратов (ДМНК).

Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, поставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 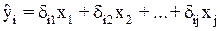и на втором шаге применительно к структурному сверхиудетифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидетифицируемая структурная модель может быть двух типов:

· все уравнения системы сверхидетифицируемы;

· система содержит наряду со сверхидетифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхиудетифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений

Применим ДМНК к простейшей сверхидетифицируемой модели:

Данная модель может быть получена из предыдущей идетифицируемой модели:

если наложить ограничения на ее параметры, а именно:

В результате первое уравнение стало сверхидетифицируемым: Н = 1 (у₁), D = 1 (х₂) и D + 1 > H. Второе уравнение не изменилось и является точно идентифицируемым: Н = 2, D = 1 и D + 1 = H.

На первом шаге найдем приведенную форму модели, а именно:

Предполагая использование тех же исходных данных, что и в предыдущем примере, получим ту же систему приведенных уравнений:

На основе второго уравнения данной системы можно найти теоретические значения для эндогенной переменной у₂, т.е. 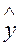. С этой целью в уравнение поставляем значения х₁ и х₂ (в нашем примере это отклонения от средних уровней). Оценки для эндогенной переменной у₂ приведены в таблице:

Дата добавления: 2016-05-16 ; просмотров: 1118 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

14. Проблема идентификации

При переходе от приведенной формы модели к структурной сталкиваются с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (3.3) в полном виде содержит параметров, а приведенная форма модели в полном виде содержит параметров. Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно параметров структурной модели не могут быть однозначно определены из параметров приведенной формы модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель Идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель Неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель Сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в I-м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, – через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

Рассмотрим Пример. Изучается модель вида

Где – расходы на потребление в период T, – совокупный доход в период T, – инвестиции в период T, – процентная ставка в период T, – денежная масса в период T, – государственные расходы в период T, – расходы на потребление в период , инвестиции в период . Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.

Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.

Модель включает четыре эндогенные переменные и четыре предопределенные переменные (две экзогенные переменные – и и две лаговые переменные – и ).

Проверим необходимое условие идентификации для каждого из уравнений модели.

Первое уравнение: . Это уравнение содержит две эндогенные переменные и и одну предопределенную переменную . Таким образом, , а , т. е. выполняется условие . Уравнение сверхидентифицируемо.

Второе уравнение: . Оно включает две эндогенные переменные и и одну экзогенную переменную . Выполняется условие . Уравнение сверхидентифицируемо.

Третье уравнение: . Оно включает две эндогенные переменные и и одну экзогенную переменную . Выполняется условие . Уравнение сверхидентифицируемо.

Четвертое уравнение: . Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.

Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.