Проблема решения уравнения навье стокса

Решение проблемы турбулентности, отсутствие аналитического решения уравнений Навье-Стокса / The solution to the pboblem of turbulence, lack of analytical solution of navier-stokes equations

Решена проблема турбулентности – показано некорректности применения модельных представлений Навье, приведена модель Колмогорова, сравнение выполнено по теореме Геделя. Получен результат, что уравнения Навье-Стокса не охватывают турбулентность. Решена проблема тысячелетия, сформулированная институтом Клея – решение уравнений Навье-Стокса на пространстве R3. То что не описывает модель Анри Навье, уравнения Навь-Стокса решить не смогут.

Оглавление

• Введение
• Проблема решения уравнений Навье-Стокса

Приведённый ознакомительный фрагмент книги Решение проблемы турбулентности, отсутствие аналитического решения уравнений Навье-Стокса / The solution to the pboblem of turbulence, lack of analytical solution of navier-stokes equations предоставлен нашим книжным партнёром — компанией ЛитРес.

Проблема решения уравнений Навье-Стокса

Уравнения Навье-Стокса, как показано в работе [1,с.73] Л.Н. Ландау, получаются записью баланса поступающей и выходящей жидкости с учетом диссипации энергии при вязком трении в жидкости. Вместе с тем, Л.Д. Ландау было отмечено, что впервые формулировка уравнений для несжимаемой жидкости была записана на основе модельных представлений Анри Навье (о молекулярных взаимодействиях).

Запишем уравнение Навье-Стокса для сжимаемой жидкости:

Для сжимаемой жидкости в уравнении

Обозначения в уравнении и его вывод — см. работу Л.Н. Ландау [1].

А.Н. Колмогоров в работе [2,с.294] показал физическую модель турбулентности (в соответствии с Тейлором и Ричардсоном), состоящую В накладывании различных по масштабу турбулентных пульсаций на осредененный поток. Наибольшим масштабом является мастшаб L «пути перемешивания», наименьшим масштабом является масштаю λ, на котором вязкость оказывает влияение. Пульсации от курупных масштабов передают энергию пульсациям меньших масштабов. В результате этого возникает поток энергии, диссипация которой происходит за счет сил вязкого торения на масштабе λ. Колмогоров предложил следующие уравнения турбулентного движения исходя из локальных свойств турбулентности [2,с.295]:

В уравнениях — обозначения согласно цитируемой работе А.Н. Колмогорова.

Л.Д. Ландау отметил [2,с.296], что эти уравнения верны для локальной струкруты турбулентности, однако в турбулентном потоке наличие ротора скорости ограничивается конечной обдастью пространства и уравнения должны показывать именно такое распределение турбулентных вихрей.

Анри Навье в работе [3] при формулировке уравнений движения жидкости исходил из записи для одной точки пространства сплошной среды.

Ландау называет представления Анри Навье модельными [2,с.73] (в сноске).

Покажем модель физической картины течения, на которой основаны уравнения Навье:

То, что описывается этой моделью, для этого может быть найдено решение уравнений Навье-Стокса. Этой моделью прекрасно можно описать частные случаи.

Сравним модель движения из работы А.Навье с моделью турбулентности, предложенной А.Н. Колмогоровым.

Некоторые авторы указывают, что уравнения Навье-Стокса содержит турбулентность. Как видно, это не так. Уравнения Навье-Стокса могут быть применены на самом низком уровне модели Колмогорова. В целом, модель Анри Навье физически некорректна по сравнению с верной моделью Колмогорова. О её верности отметил Ландау [1,с.296] (на рассмотрении присутствовал Капица).

Главная проблема — уравнения Навье не предназначены для турбулентности и решения на пространстве R3, где турбулентность по-умолчанию есть (хотя и не оговаривается).

Метод DNS работает почти как модель Колмогорова, только энергия считается не сверху вниз, а снизу вверх (от ячеек до интегрального масштаба). Отсюда видно, почему численно легко уравнения Навье-Стокса решаются по DNS.

Объем, для которого составляются уравнения Навье-Стокса выбран с минимальными размерами, обеспечивающими сплошность среды. Однако это не принципиально. Очевидно, что куб несопоставимо меньше пространства R3.

Для куба описание физического процесса состоит в описании поступления в него и выхода из него жидкости, а также влияния вязкости.

Для пространства R3 со сложной структурой турбулентного течения физический процесс намного более сложен и для его описания недостаточно тех описаний, которые применены для куба при выводе уравнений Навье-Стокса!

В существующих попытках решения уравнений Навье-Стокса пространство R3 условно разбивают (дискретизируют) сеткой с кубичиескими элементами.

Попытки аналитического решения, например, в работе [4], сводятся к назначению граничных условий для уравнений и поиску решений.

Граничные условия для куба со сторонами x, y, x и шагом Q записываютcя в виде:

Очевидно, что движение жидкости в пространстве R3 и в любом пространстве, моделью Навье и его представлениями не описывается. Область вокруг точки не превышает колмогоровского масштаба.

Уравнения Навье-Стокса сооставлены для физической модели мелкого колмогоровского масштаба и не соответсвуют физическим процессам турбулентного движения больших объемов жидкости.

В случае аналитически точного решений Уравнений Навье-Стокса для случая течения Пуазёйля, решение выполняется для физического процесса, описываемого процесс для куба.

Существут методы прямого численного решения уравнений Навье-Стокса [5], [6], [7].

В этих методах (конечно-разностных) выполняется дискретизация пространства сеткой. Производная заменяется на алгебраическое отношение.

Очевидно, что в численных методах для пространства R3 решаются уравнения Навье-Стокса, не описывающие физического процесса на пространстве R3. Однако, результаты решений для каждого сеточного куба переносятся для интегрального решения для всей сетки, т.е. для пространства R3.

Для модели турбулентности Колмогорова такой подход означал бы расчет рассеянной энергии на всех мелких масштабах и суммирование полученных значений для верхнего масштаба. Модель Колмогорова описывает реальную картину течения жидкости.

Ошибка в численных методах решения находится в самом их теоретическом основании. Решается модель с физическим процессом, не описывающим течение на пространстве R3, для каждой ячейки сетки и затем получения результата расчета для всей сетки, а следовательно и для пространства R3. То есть к решению на пространстве R3 в численном методе применяется некорректная физическая модель, которая не описывает процессов на пространстве R3.

Существование и гладкость решений уравнений Навье — Стокса

Вы будете перенаправлены на Автор24

Существование и гладкость решений уравнений Навье — Стокса – это задача из области математики, которую в 2000 году Математический институт Клэя признал шестой из семи задач тысячелетия.

Для данной проблемы есть, как математические доказательства существования и единственности решения задачи с периодическими граничными условиями, так и доказательства потери единственности решений при резком возникновении неустойчивости в конечное время.

Уравнения Навье-Стокса – это математическая модель движения вязкой несжимаемой жидкости. Интерес представляют не все решения этих уравнений, а только те, которые годятся для описания реальных течений.

Данные уравнения стали основой гидродинамики. Численные решения этих уравнений применяются во многих практических случаях. Аналитически данные уравнения решены только для некоторых частных задач. Отсутствует понимание полностью свойств уравнений Навье-Стокса.

Уравнения Навье — Стокса

В трехмерном случае уравнения Навье — Стокса можно записать как:

$\frac<\partial \vec v><\partial t>+(\vec v \nabla )\vec v = \frac<1> <\rho>\nabla p+\nu \Delta \vec v+\vec f (\vec r , t)(1),$

• $\vec v$ — трехмерный вектор скорости;
• $p$ — давление;
• $\nu$ > $0$ — кинематическая вязкость,
• $\rho$ — плотность;
• $\vec f$ — внешняя сила;
• $\nabla$ — оператор набла;
• $\Delta$ — лапласиан.

Уравнение (1) является векторным. Его можно представить в виде системы из трех скалярных уравнений.

В данном уравнении следует найти поле скоростей и давлений. Так как в трехмерном случае мы имеем три уравнения и четыре неизвестных, то дополнительно используют уравнение неразрывности, которое для несжимаемой жидкости записывают как:

Готовые работы на аналогичную тему

$\nabla \bullet \vec v=0 (2).$

Начальные условия к уравнениям можно задать в виде поля скоростей в момент времени $t=t_0$:

$\vec v (\vec r, 0)=\vec v_0(\vec r),$

где $\vec v_0(\vec r)$ — известная гладкая векторная функция, которая должна удовлетворять уравнению неразрывности (2).

Уравнения Навье — Стокса в гидродинамике

Точные решения уравнений Навье — Стокса обладают большим значением в теоретической гидродинамике. Этим решениям посвящают множество научных работ.

Задача математической физики считается поставленной корректно, если дополнительные условия, начальные и краевые обеспечивают:

1. существование решения;
2. его единственность,
3. непрерывную зависимость от заданных в задаче параметров.

Если принимать во внимание сказанное выше, то корректными в гидродинамике являются задачи, которые можно отнести к течениям с малыми числами Рейнольдса, когда нелинейность уравнений не проявляется.

При увеличении числа Рейнольдса проявляется нелинейность, и появляются свойства, которые нельзя совместить с определением корректности.

Для стационарных задач нелинейность может вызывать неединственность решения при одних числах Рейнольдса и его отсутствие при других.

Возможность решения задачи в гидродинамике принципиальным образом зависит от ее постановки, то есть от:

• начальных условий;
• краевых условий.

Классическими граничными условиями в гидродинамике являются следующие виды условий:

1. Условия прилипания для ограниченной области, которые связаны с заданием вектора скорости на границе, который удовлетворяет только условию соленоидальности.
2. Условия в бесконечной области для задач обтекания. В этом случае на обтекаемой границе задают условия прилипания, в бесконечности вектор скорости постоянен.
3. Условия на свободных границах.

В задаче обтекания постоянство вектора скорости в бесконечности является обязательным.

Наряду с указанными граничными условиями принципиально возможны и другие разнообразные постановки. Например, циркуляционное течение вязкой жидкости в круговой области, на границе которой заданы условия непротекания и отсутствия касательных напряжений. Решение данной задачи является неединственным, так как квазитвердое вращение с произвольной угловой скоростью удовлетворяет всем условиям задачи.

Строгие теоретические решения уравнений Навье-Стокса, в основном получены для граничных условий первого и второго типа. О.А. Ладыженской доказано, что стационарная задача с граничными условиями первого или второго вида имеет, по крайней мере, одно гладкое решение при любых числах Рейнольдса. В этом случае граница области и граничные условия не обязательно являются гладкими. Но при этом необходимо ограниченность значений вектора скорости на границе и массовых сил в общем случае.

Проблема единственности стационарных решений снята только для случая малых чисел Рейнольдса. В иных случаях неединственность решений – это скорее правило, чем исключение.

Особым вниманием в стационарной гидродинамике пользуется предельный переход $\nu \to 0$. В виду тог, что самые распространенные вещества – вода и воздух – обладают малыми кинематическими вязкостями в сравнении с характерными параметрами $V L$, где $L$ — линейный масштаб течения. Асимптотическую постановку этой задачи дала теория пограничного слоя Прандтля и ее расширение – теория сращиваемых асимптотических разложений. Заметим, что схема Прандтля применима не всегда.

Разрешимость начально-краевых нестационарных задач доказана для всех моментов времени только в случае двух пространственных измерений. В общем трехмерном случае разрешимость доказана для гладких начальных данных на малом временном интервале.

Вопрос об однозначности разрешимости трехмерной задачи в «целом» для любого времени, любых гладких данных задачи и любых размеров области течения открыт по настоящее время.

Так, имеется «слабое» решение Хофа, но класс «слабых» решений недопустимо широк, поскольку в нем происходит нарушение течения, а это несовместимо с принципом детерминизма в классической механике.

Если допускать существование «хорошего» решения в целом, то доказывается :

• его единственность,
• непрерывная зависимость нестационарных решений от начальных данных и внешних сил для конечных временных интервалов.

В классе двумерных задач с нулевыми граничными условиями это доказано для произвольного интервала (так, при нулевых условиях и убывании сил движение жидкости затухает).

Для задач с неоднородными условиями непрерывной зависимости решения в целом от начальных условий нет, так как при больших числах Рейнольдса стационарные течения способны терять устойчивость.

Постановка задачи институтом Клэя

Математический институт Клэя выдвинул два базовых варианта условий задачи для решений уравнений Навье-Стокса:

1. Решение уравнений в трехмерном пространстве учитывая ограничения скорости роста решения в бесконечности. Для любых начальных условий.
2. Решение данных уравнений на торе в пространстве трех измерений. При этом граничные условия должны быть периодическими.

Задача будет считаться решенной, если будет доказано наличие или отсутствие решения и его гладкость или негладкость.

Математики нашли проблему в знаменитых уравнениях для описания жидкостей

Два математика доказали, что при определённых экстремальных условиях уравнения Навье-Стокса выдают бессмыслицу

Уравнения Навье-Стокса при помощи нескольких лаконичных членов описывают одно из самых распространённых явлений физического мира: течение жидкостей. Сегодня эти уравнения, появившиеся ещё в 1820-х, используются для описания всего, от океанских течений и турбулентности, следующей за самолётом до потока крови в сердце.

Хотя физики считают эти уравнения надёжными, как молоток, математики относятся к ним с недоверием. Для математика то, что эти уравнения вроде бы работают, мало что значит. Им нужны доказательства того, что уравнения безошибочны: что для любой жидкости и для долгосрочного прогноза, распространённого сколь угодно далеко в будущее, математика уравнений не подведёт. Такую гарантию оказалось нелегко отыскать. Первый человек или команда, которая сумеет доказать, что уравнения Навье-Стокса будут работать всегда — или представить пример, доказывающий, что они не работают — сможет получить награду за решение одной из «Задач тысячелетия», анонсированных математическим институтом Клэя, и миллионом долларов в придачу [по состоянию на 2017 год только одна из семи задач тысячелетия (гипотеза Пуанкаре) решена Григорием Перельманом / прим. перев.].

Математики разработали множество способов для решения этой задачи. Новая работа, опубликованная в сентябре, ставит серьёзные вопросы по поводу того, сможет ли добиться успеха один из самых популярных подходов к задаче, разрабатываемый в течение многих лет. Работа, которую написали Тристан Бакмастер и Влад Викол из Принстонского университета, представляет собой первый результат, показывающий, как при определённых условиях уравнения Навье-Стокса дают противоречивое описание физического мира.

«Мы пытаемся понять определённые проблемы, присущие этим уравнениям, и то, почему людям, вероятно, придётся их переосмыслить», — говорит Бакмастер.

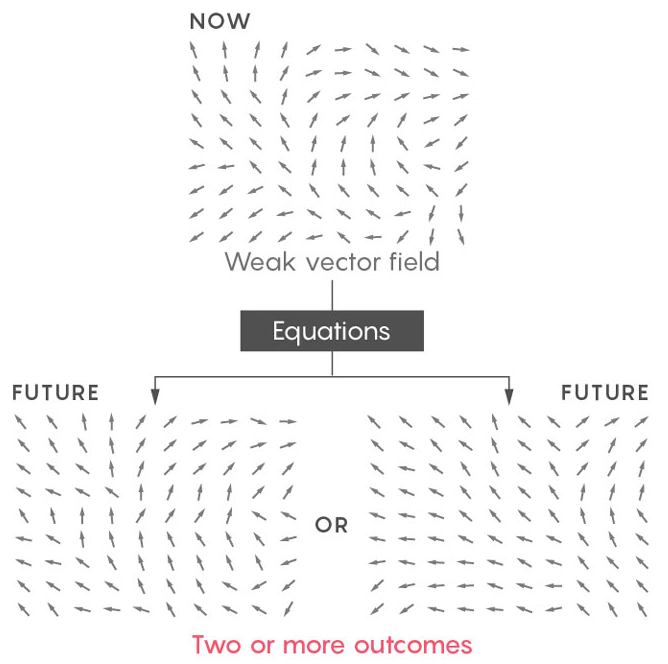
Работа Бакмастера и Викола показывает, что, если принять при решении уравнений Навье-Стокса очень грубые допущения, они начинают выдавать бессмыслицу: утверждают, что одна и та же жидкость с одними и теми же начальными условиями может прийти в два или более различных состояний. Она может течь одним образом, или же совершенно другим. Если так, то эти уравнения не могут надёжно описывать физический мир, для которого они были разработаны.

Взрывая уравнения

Чтобы понять, как уравнения могут сломаться, представьте себе океанское течение. В его рамках могут существовать локальные течения, в результате чего некоторые его части могут перемещаться в одном направлении и с одной скоростью, а другие — в другом направлении с другой скоростью. Локальные течения взаимодействуют друг с другом в постоянном взаимном действии трения и давления воды, определяющих её поток.

Математики моделируют это взаимодействие при помощи карты, сообщающей вам о направлениях и скорости потока в любой точке жидкости. Эта карта, называемая векторным полем — снимок внутренней динамики жидкости. Уравнения Навье-Стокса берут этот снимок и воспроизводят его, как видео, сообщая, как именно будет выглядеть векторное поле в каждый последующий момент времени.

Карта ветров (windy.com) работает похожим на векторное поле образом. В каждой точке у ветра есть определённое направление и сила

Эти уравнения работают. Они описывают течение жидкости так же надёжно, как уравнения Ньютона предсказывают будущие положения планет; физики постоянно используют их, и они постоянно совпадают с результатами экспериментов. Однако математикам нужно нечто большее, чем эпизодическое подтверждение — им нужно доказательство того, что уравнения не нарушаются, что вне зависимости от того, с какого векторного поля вы начнёте, и от того, как далеко в будущее вы будете его воспроизводить, уравнения всегда дадут вам новое, уникальное векторное поле.

Это и есть тема Задачи тысячелетия, спрашивающей, есть ли у уравнений Навье-Стокса решения (решение, по сути, и есть векторное поле) для всех начальных точек во все моменты времени. Эти решения должны обеспечить точное направление и силу потока в каждой точке жидкости. Решения, дающие информацию с таким бесконечно мелким разрешением, называются «гладкими». У гладкого решения каждая точка поля имеет связанный с ней вектор, позволяющий вам «гладко» путешествовать по полю, не застревая в точках, где вектор отсутствует — в точке, дальнейшее движение из которой вам будет непонятно.

Гладкие решения — полное представление физического мира, но с математической точки зрения они могут существовать не всегда. Математики, работающие над уравнениями, подобными этим, переживают по поводу такой ситуации: вы запускаете уравнения Навье-Стокса и наблюдаете за изменениями векторного поля. По прошествии какого-то конечного времени уравнения говорят вам, что некая частица жидкости двигается с бесконечной скоростью. Тогда у вас будут проблемы. В уравнения входит измерение изменений таких свойств, как давление, трение, скорость жидкости — говоря жаргонным языком, они берут производные этих величин — но производную от бесконечной величины взять не проще, чем поделить на ноль. Так что если уравнения выдают бесконечное значение, можно сказать, что они отказали вам, или «взорвались». Они уже не могут описывать последующие состояния вашей жидкости.

Такой «взрыв» — свидетельство того, что в уравнениях не хватает описания каких-то свойств физического мира, который они должны описывать. «Возможно, уравнения охватывают не все эффекты реальной жидкости, поскольку в реальной жидкости мы не ожидаем» бесконечной скорости движения частиц, как говорит Бакмастер.

Решение Задачи тысячелетия состоит либо в том, чтобы показать, что уравнения Навье-Стокса никогда не взрываются, либо найти условия, при которых это происходит. Одна из стратегий, используемых математиками — смягчить требования к тому, как точно эти уравнения должны описывать требуемые решения.

Нарушение потока

Уравнения Навье-Стокса должны описывать течение любой жидкости, с любыми начальными условиями, и распространять описание бесконечно далеко в будущее. Пытаясь доказать эту их способность, математики иногда «ослабляют», то есть, используют приближённые описания векторных полей, описывающих жидкость. Но с этим возникают трудности.

В идеале, математики хотят доказать, что применение уравнений Навье-Стокса к любой непрерывной, «гладкой» жидкости выдаст один уникальный результат.

Однако проще работать со «слабыми», не такими детализированными векторными полями. И вот математики обнаружили, что некоторые слабые описания выдают неуникальные результаты — позволяют одной и той же жидкости в одних и тех же начальных условиях течь двумя способами.

От слабых к гладким

Когда математики изучают такие уравнения, как эти, они иногда начинают расширять определение того, что считается решением. Гладким решениям требуется максимум информации — в случае с Навье-Стоксом им требуется, чтобы в каждой точке векторного поля, связанного с жидкостью, существовал вектор. Но что, если ослабить требования, и сказать, что вам нужно подсчитывать вектора только для некоторых точек поля, или нужно получить только примерные значения векторов? Такие решения называют «слабыми». Они позволяют математикам почувствовать поведение уравнения без утомительной работы по поиску абсолютно всех решений (что на практике может оказаться и невозможным).

Тристан Бакмастер, математик из Принстонского университета

«С какой-то точки зрения слабые решения ещё легче описать, чем реальные, поскольку знать нужно гораздо меньше», — сказал Камилло Де Леллис, в соавторстве с Лазло Щекелихиди написавший несколько важных работ, заложивших фундамент для работы Бакмастера и Викола.

Слабые решения бывают разной градации. Если представить себе гладкое решение в виде математического изображения жидкости с бесконечным разрешением, то слабые решения будут представлять собой нечто вроде 32-битных, 16-битных или 8-битных версий этого изображения.

В 1934 году французский математик Жан Лере определил важный класс слабых решений. Вместо работы с точными векторами, «решения Лере» берут среднее значение векторов в небольшой окрестности векторного поля. Лере доказал, что всегда можно решить уравнения Навье-Стокса, позволяя вашим решениям принимать форму такого вида. Иначе говоря, решения Лере не взрываются.

Достижение Лере определило новый подход к задаче Навье-Стокса: начать с решений Лере, о существовании которых уже известно, и посмотреть, можно ли превратить их в гладкие решения, существование которых вы хотите доказать. Этот процесс напоминает тот, где вы начинаете с грубой картинки, и смотрите, нельзя ли постепенно подкрутить разрешение, чтобы достичь идеального изображения реальности.

«Одна из возможных стратегий — показать, что эти слабые решения Лере гладкие, и если вы сможете показать, что они гладкие — вы решите Задачу тысячелетия», — сказал Бакмастер.

Влад Вкол представляет собой половину команды, вскрывшей проблемы в подходе к проверке уравнений Навье-Стокса.

Есть и ещё один подвох. Решения уравнений Навье-Стокса соответствуют реальным физическим событиям, а физические события происходят одним возможным образом. Учитывая это, хотелось бы, чтобы у ваших уравнений был только один набор уникальных решений. Если уравнения дают вам множество возможных решений, они не справляются со своей задачей.

Поэтому математики смогут использовать решения Лере для решения Задачи тысячелетия, только если решения Лере уникальны. Неуникальные решения Лере будут означать, что, согласно правилам Навье-Стокса, одна и та же жидкость с одними и теми же начальными условиями может прийти к двум разным физическим состояниям, что не имеет физического смысла, и подразумевает, что уравнения на самом деле не описывают то, что должны.

Новый результат Бакмастера и Викола — первый намёк на то, что для определённых определений слабых решений может происходить именно это.

Множество миров

В своей новой работе Бакмастер и Викол рассматривают ещё более слабые решения, чем решения Лере — решения, в которых используется тот же принцип усреднения, что у и Лере, но ослаблено ещё одно дополнительное требование (известное, как неравенство энергий). Они используют метод «выпуклого интегрирования», берущий начало из работ по геометрии математика Джона Нэша, и позднее привлечённый к изучению жидкостей Де Леллисом и Щекелихиди.

Используя такой подход, Бакмастер и Викол доказывают, что эти очень слабые решения уравнений Навье-Стокса неуникальны. Они, к примеру, демонстрируют, что если начать с полностью спокойной жидкости, к примеру, со стакана с водой рядом с кроватью, возможны два вида развития событий. Первый очевиден: вода начинает со спокойного состояния и остаётся спокойной всегда. Второй фантастичный, но математически возможный: вода начинает со спокойного состояния, взрывается в середине ночи, а затем возвращается в спокойное состояние.

«Это доказывает отсутствие уникальности, поскольку из начальных данных можно сконструировать по меньшей мере два объекта», — говорит Викол.

Бакмастер и Викол доказали существование множества неуникальных слабых решений (не только тех двух, что описаны выше) уравнений Навье-Стокса. Важность этого доказательства ещё предстоит понять. В какой-то момент слабые решения могут стать настолько слабыми, что они перестанут быть связанными с более гладкими решениями, которые должны имитировать. Если так и есть, тогда результат, полученный Бакмастером и Виколом, мало к чему приведёт.

«Такой результат однозначно является предупреждением, но можно спорить о том, что это предупреждение касается самой слабой идеи слабых решений. Существует множество слоёв более сильных решений, на гораздо лучшее поведение которых можно возлагать надежду» в случае уравнений Навье-Стокса, — говорит Де Леллис.

Бакмастер и Викол также мыслят в терминах слоёв, и он нацелились на решения Лере — на доказательство того, что и те допускают множественную физику, в которой одна и та же жидкость из одного и того же состояния может прийти к разным формам в будущем.

«Мы с Тристаном считаем, что решения Лере неуникальны. Мы пока этого не доказали, но наша работа закладывает плацдарм для атаки на эту задачу», — сказал Викол.