Проект по теме системы уравнений

Исследовательский проект на тему: «Системы уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Системы уравнений
Проект выполнил
ученик 9 класса Б
МАОУ лицея №20

Руководитель проекта
Поличева Н.М.

Как научится решать системы уравнений с двумя переменными из ОГЭ по математике?

Проблема проекта:
Добавить нижний колонтитул
2

Цели:
1)Осознать и осмыслить различные способы решения систем уравнений с двумя переменными.
2)Решить задачи и уравнения, которые представлены в ОГЭ.
3)Сделать вывод о проделанной работе .

Задачи:
1) Вспомнить все виды решения уравнений.
2) Через решение уравнений и задач развить творческую и мыслительную деятельность учащихся.
3) Научиться решать и проверять результаты своей деятельности.

Определение:
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменны.
Добавить нижний колонтитул
5

История уравнений
Уравнение с двумя неизвестными выражает зависимость между двумя величинами , имеет бесчисленное множество решений и является неопределенным.
Решением таких уравнений занимались в древности китайцы, греки и индийцы.
В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.

Добавить нижний колонтитул
6

Задачи на составление и решение систем уравнений встречаются в вавилонских и египетских текстах 2 тысячелетия до н.э., в трудах древнегреческих, китайских и индийских ученых. Нижние индексы при буквах впервые употребил в 1675 г. немецкий математик Лейбниц.

Добавить нижний колонтитул
7

Основные методы решения систем уравнений
И
1. Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.

2. Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.

3.Метод решения уравнения с системой графическим способом.
шаблона
4. Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы. обратная связь
8

Добавить нижний колонтитул
14
Вывод:
Работа над проектом, используя учебные пособия, а также применение полученных знаний на практике – это реальная возможность решить задание № 21 и подготовиться к ОГЭ по математике, и сдать его на хорошую оценку.

https://oge.sdamgia.ru/
https://www.google.com/search
Учебник Алгебры Ларин ОГЭ
Консультация с педагогом по математике
Учебник Алгебры 9 класс Мордкович
https://www.google.com/search

Список литературы:
Добавить нижний колонтитул
15

Спасибо за внимание

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 939 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 589 437 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 01.04.2021
• 182
• 3

• 01.04.2021
• 194
• 3

• 01.04.2021
• 170
• 0

• 01.04.2021
• 130
• 0

• 01.04.2021
• 118
• 0

• 01.04.2021
• 118
• 1

• 01.04.2021
• 195
• 4

• 01.04.2021
• 129
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.04.2021 340
• PPTX 2.6 мбайт
• 22 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Поличева Наталья Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 5 месяцев
• Подписчики: 36
• Всего просмотров: 48008
• Всего материалов: 75

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Студенты российских вузов смогут получить 1 млн рублей на создание стартапов

Время чтения: 3 минуты

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

«Системы линейных уравнений».
проект по алгебре (7 класс) по теме

Реализация требований ФГОС ООО при обучении учащихся 7 класса теме: «Системы линейных уравнений».

Скачать:

Предварительный просмотр:

Государственное бюджетное образовательное учреждение высшего профессионального

образования МО «Академия социального управления»

Дополнительное профессиональное образование

Кафедра математических дисциплин

Реализация требований ФГОС ООО при обучении учащихся 7 класса

теме: «Системы линейных уравнений»

слушатель учебного курса

«Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС)»

учитель математики МАОУ лицей № 14 им. Ю.А. Гагарина

Щёлковского муниципального района Московской области

Гудкова Алла Борисовна

к.п.н. доцент кафедры

Ерина Татьяна Михайловна

ГЛАВА 1. Теоретические основы обучения теме «Системы линейных уравнений».

§ 1. Эссе «Концепции духовно-нравственного развития и воспитания личности гражданина России»

§ 2. Логико-математический анализ содержания темы «Системы линейных уравнений»

§ 3. Цели обучения теме «Системы линейных уравнений»

3.1. Развитие познавательных УУД

3.2. Развитие регулятивных УУД

3.3. Развитие коммуникативных УУД

3.4. Развитие личностных УУД

ГЛАВА 2. Методические рекомендации обучения теме «Системы линейных уравнений».

§ 4. Карта изучения темы и её использование

4.1. Диагностируемые цели обучения теме «Системы линейных уравнений»

4.2. Логическая структура и содержание темы «Системы линейных уравнений»

4.3. Средства обучения теме (в том числе ИТ)

§ 5. Учебный план темы «Системы линейных уравнений».

§ 6. Примеры реализации целей обучения теме «Системы линейных уравнений»

Цель проекта : Реализация требований ФГОС ООО при изучении темы:

Для достижения поставленной цели необходимо решение следующих задач.

1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.

2. Выполнить отбор средств обучения теме, в том числе средства ИКТ

3. Разработать таблицу целей и карту обучения теме.

4. Составить учебную рабочую программу « Тематическое и почасовое планирование образовательных результатов освоения математики (в соответствии с темой).

5. Разработать методические рекомендации обучения теме и применить их в учебном процессе (фрагментов двух – трёх уроков, иллюстрирующих развитие и формирование УУД при обучении данной теме школьного курса математики).

Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.

§ 1. Эссе «Концепции духовно-нравственного развития и воспитания личности гражданина России»

Н.А. Бердяев писал: «Высшие цели жизни не экономические и не социальные, а духовные. Величие народа, его вклад в историю человечества определяется не могуществом государства, не развитием экономики, а духовной культурой».

Образованию отводится ключевая роль в духовно-нравственной консолидации российского общества, в его сплочении перед лицом внешних и внутренних вызовов, в укреплении социальной солидарности, в повышении уровня доверия человека к жизни в России, к согражданам, обществу, государству, настоящему и будущему своей страны.

Наиболее системно, последовательно и глубоко духовно-нравственное развитие и воспитание личности происходит в сфере общего образования, где развитие и воспитание обеспечено всем укладом школьной жизни.

Новая российская общеобразовательная школа должна стать важнейшим фактором, обеспечивающим социокультурную модернизацию российского общества.

Именно в школе должна быть сосредоточена не только интеллектуальная, но и гражданская, духовная и культурная жизнь школьника. Отношение к школе как единственному социальному институту, через который проходят все граждане России, является индикатором ценностного и морально-нравственного состояния общества и государства.

Концепция представляет собой ценностно-нормативную основу взаимодействия общеобразовательных учреждений с другими субъектами социализации – семьёй, общественными организациями, религиозными объединениями, учреждениями дополнительного образования, культуры и спорта, средствами массовой информации. Целью этого взаимодействия является совместное обеспечение условий для духовно-нравственного развития и воспитания обучающихся.

• характер современного национального воспитательного идеала;

• цели и задачи духовно-нравственного развития и воспитания детей и молодежи;

• систему базовых национальных ценностей, на основе которых возможна духовно-нравственная консолидация многонационального народа Российской Федерации;

• основные социально-педагогические условия и принципы духовно-нравственного развития и воспитания обучающихся.

Общеобразовательные учреждения должны воспитывать гражданина и патриота, раскрывать способности и таланты молодых россиян, готовить их к жизни в высокотехнологичном конкурентном мире. При этом образовательные учреждения должны постоянно взаимодействовать и сотрудничать с семьями обучающихся, другими субъектами социализации, опираясь на национальные традиции.

Концепция формулирует социальный заказ современной общеобразовательной школе как определённую систему общих педагогических требований, соответствие которым обеспечит эффективное участие образования в решении важнейших общенациональных задач.

Важнейшей целью современного отечественного образования и одной из приоритетных задач общества и государства является воспитание, социально-педагогическая поддержка становления и развития высоконравственного, ответственного, творческого, инициативного, компетентного гражданина России.

Духовно-нравственное развитие и воспитание личности начинается в семье. Семейные ценности, усваиваемые ребенком с первых лет жизни, имеют непреходящее значение для человека в любом возрасте. Взаимоотношения в семье проецируются на отношения в обществе и составляют основу гражданского поведения человека.

Следующая ступень развития гражданина России – это осознанное принятие личностью традиций, ценностей, особых форм культурно-исторической, социальной и духовной жизни его родного села, города, района, области, края, республики. Через семью, родственников, друзей, природную среду и социальное

окружение наполняются конкретным содержанием такие понятия, как «малая Родина», «Отечество», «родная земля», «родной язык», «моя семья и род», «мой дом».

Более высокой ступенью духовно-нравственного развития гражданина России является принятие культуры и духовных традиций многонационального народа Российской Федерации.

Духовно-нравственное развитие и воспитание обучающихся должны быть интегрированы в основные виды деятельности обучающихся: урочную, внеурочную, внешкольную и общественно полезную.

В МАОУ лицей № 14 имени Ю.А. Гагарина большое внимание уделяется духовно-нравственному развитию обучающихся: на уроках, в процессе внеурочной деятельности внедряется социокультурная программа «Истоки», проводится большая работа по патриотическому воспитанию, к которой привлекаются ветераны Великой Отечественной войны и воины-интернационалисты. В школе создан замечательный музей боевой славы «Чкаловцы». Учащиеся 4 классов осваивают программу «Основы религиозной культуры и этики», а ученики 5 и 8 классов изучают предмет «Родное Подмосковье».

Воспитание человека, формирование свойств духовно-развитой личности, любви к своей стране, потребности творить и совершенствоваться есть важнейшее условие успешного развития России.

§ 2. Логико-математический анализ содержания темы.

Образовательными и воспитательными целями при обучении учащихся 7 класса теме «Системы линейных уравнений» является;

• продолжение формирования представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
• продолжение овладения математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественных дисциплин;
• раскрытие конструктивной природы математических понятий;

• построение системы математических правил на основе логической связи их между собой;
• раскрытие операционного состава единого математического приема неполной индукции, используемого при доказательстве основного содержания изучаемой темы;
• воспитание средствами математики культуры личности,
• понимание значимости математики для научно-технического прогресса;
• отношение к математике как к части общечеловеческой культуры через знакомство с историей развития математики.

Ориентация учебного процесса на достижение данных целей позволяет учителю концентрировать внимание на главном, определять порядок и перспективы работы, осуществлять ясность и гласность в совместной работе учителя и учащихся. Это дает учителю возможность разъяснять учащимся ориентиры в их общеучебной работе, создавать эталоны оценки результатов обучения.

Материал данной темы составляет важную часть школьного курса математики, что и определяет цели ее изучения: в процессе обучения происходит

ознакомление обучающихся с основами наук; развивается логическое мышление, формируются и закрепляются вычислительные навыки. Материал данной темы находит широкое применение при изучении других тем школьного курса математики, так же и других смежных дисциплин, помогают тем самым реализовать межпредметные связи.

Изучение данной темы способствует развитию алгоритмической культуры, критичности мышления. В процессе обучения закрепляется, углубляется и повторяется пройденный материал, решаются разнообразные практические задачи.

При изучении теме «Системы линейных уравнений» можно выделить основные направления ее развертывания в школьном курсе математики:

• теоретико — математическая, которая раскрывается в двух аспектах: в изучении наиболее важного класса линейных уравнений, в изучении обобщенного приема и методов решения систем линейных уравнений.
• эффективное средство закрепления, углубления, повторения и расширения теоретических знаний;
• развитие творческой математической деятельности обучающихся.

Для обучения данной темы по учебнику: Макарычев Ю.Н., Миндюк Н.Г.,

Нешков К.И., Суворова С.Б. «Алгебра 7 класс» отводится 17 часов при 4 уроках алгебры в неделю.

1) П 40. Линейное уравнение с двумя переменными – 2 часа;

2) П 41. График линейного уравнения с двумя переменными – 2 часа;

3) П 42. Системы линейных уравнений с двумя переменными – 2 часа;

4) П 43. Способ подстановки – 3 часа;

5) П 44 Способ сложения – 2 часа;

6) П 45 Решение задач с помощью систем уравнений – 5 часов;

Контрольная работа – 1 час.

Обучение теме «Глава VI Системы линейных уравнений» начинается с создания положительной мотивации к ее изучению. Познавательным мотивом является рассмотрение проблемы решения уравнений в натуральных числах в

работах известного греческого математика Диофанта (III в.), в связи с чем уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называют диофантовыми уравнениями. Учебно–познавательным мотивом является интерес к решению текстовых задач алгебраическим способом. Очень важны для обучающихся 7 класса узкие социальные мотивы: овладение способом налаживания сотрудничества в учебном труде. Учебно — познавательными действиями при обучении данной темы является распознавание, сравнение, сопоставление, конкретизация общего способа решения для данного типа задач.

Основной учебной задачей при изучении темы «Системы линейных уравнений» является формирование понятий:

• линейное уравнение ( Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где x и y – переменные, a, b и c – некоторые числа ) ;
• решение уравнения ( Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство );
• равносильные уравнения ( Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными).
• свойства уравнений

( если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному);

• график уравнения ( графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых

• являются решениями этого уравнения; графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая );
• решение системы уравнений ( решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет. );
• способ подстановки

1. выражают из какого-нибудь уравнения системы одну переменную через другую;

1. подставляют в другое уравнение системы вместо этой переменной полученное выражение;
2. решают получившееся уравнение с одной переменной;
3. находят соответствующее значение второй переменной );

• способ сложения

1. умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

1. складывают почленно левые и правые части уравнений системы;
2. решают получившееся уравнение с одной переменной;
3. находят соответствующее значение второй переменной );

• решение задач с помощью систем уравнений

1. обозначают некоторые неизвестные числа буквами и, используя условие задачи, составляют систему уравнений;

1. решают систему;
2. истолковывают результат в соответствии с условием задачи ).

Для осознанного усвоения алгоритма решения линейных уравнений можно начинать со схемы уравнения и определения его компонентов, определяя логическую цепочку в конструировании определения понятия.

Линейное уравнение с одной переменной:

1. уравнение и
2. стандартный вид: ах + в=0 , где а, в – числа, х – переменная.

Решение линейного уравнения:

то х – любое число

Прием саморегуляции при решении систем линейных уравнений.

Прием выполнения заданий типа: решить систему уравнений

Выбрать способ решения системы уравнений.

Какие способы решения системы уравнений я знаю?

Вспомнить алгоритм выбранного способа решения.

Знаю ли я алгоритм выбранного способа решения системы уравнений?

Выяснить какие свойства уравнений необходимо применить в процессе решения системы выбранным способом.

Знаю ли я свойства уравнений с двумя переменными?

Выполнить необходимые преобразования.

Полезно указать соответствующее свойство при выполнении преобразований.

Знаю ли я как делать проверку?

Знаю ли я как записывать ответ?

Линия уравнений в курсе алгебры 7 класса имеет не только важное теоретическое значение, но и служит практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различного вида уравнений и систем уравнений.

Преемственность в работе над задачей в курсе математике реализуется посредством эвристического алгоритма на всех этапах решения задачи:

1 этап – анализ содержания задачи;

2 этап – моделирования условия;

3 этап – выделение опорных знаний и основных задач ;

4 этап – моделирование решения задачи;

5 этап – подведение итогов по решению задачи;

6 этап – выполнение возможных обобщений.

Образовательные цели/задачи при обучении темы «Системы линейных уравнений»:

• иметь представление о правилах решения уравнений и систем уравнений;
• овладеть умением решать сложные системы уравнений различными способами, решать текстовые задачи на составление систем уравнений.

Для создания положительной мотивации при изучении темы можно предложить занимательные задачи, которые решаются с помощью систем уравнений, интересные факты из истории математики по теме «Системы линейных уравнений».

Анализ задачного материала темы

По характеру требований

По сложности (I, II, III уровни)

По способу решения

По дидактической цели

Задачи представлены математическим
текстом.

Распознать линейное уравнение.

Найти решение линейного уравнения.

№ 1030-1034 – на применение свойств уравнений.

№ 1036 — задание с параметром.

Отработка понятий:
линейное уравнение, решение линейного уравнения, свойства уравнений.

Решить практическую задачу.

Решение текстовых задач с помощью уравнений.

Отработка решения задач с помощью уравнения с двумя переменными в натуральных числах.

Задачи представлены математическим
текстом.

Определить принадлежность данной точки графику уравнения

Отработка понятия график линейного уравнения.

Задачи представлены математическим
текстом.

Построить график уравнения

На построение графика уравнения.

Отработка навыка построения графика уравнения

Задачи представлены математическим
текстом.

Найти координату точки по заданной второй координате

№ 1053 – на определение расположения графика уравнения в координатных четвертях

Отработка навыка нахождения координаты точки по заданной координате

Задачи представлены математическим текстом.

Проверить, является ли пара чисел решением системы уравнений.

Выяснить, сколько решений имеет система уравнений.

Отработка понятия решение системы уравнений

Задачи представлены математическим текстом.

Решить систему уравнений

Отработка графического способа решения систем уравнений.

Задачи представлены математическим текстом.

Решить систему уравнений.

Отработка способа подстановки.

Задачи представлены математическим текстом.

Решить систему уравнений.

II – 1086, 1092-1096

Отработка способа сложения.

Старинные задачи: №1104, 1105, 1115

Отработка способов решения систем уравнений при решении текстовых задач

§ 3. Цели обучения теме «Системы линейных уравнений»

За последние десятилетия в обществе произошли кардинальные изменения в представлении о целях образования и путях их достижения. В жизни каждого человека необходимостью и реальностью становится непрерывное образование. В общественном сознании происходит переход от понимания социального предназначения школы как задачи простой передачи знаний, умений и навыков от учителя к ученику к новому пониманию функции школы. Приоритетной целью школьного образования становится развитие у учащихся способности самостоятельно ставить учебные цели, проектировать пути их достижения, контролировать и оценивать свои достижения. Иначе говоря, формирование умения учиться. В связи с этим Стандартом второго поколения предусмотрено прежде всего формирование у учащихся универсальных учебных действий.

Выделяются четыре вида УУД: 1) личностные; 2) регулятивные; 3) общепознавательные; 4) коммуникативные.

1. Личностные универсальные учебные действия включают: смысло-образование, нравственно-этическое оценивание, самопознание и самоопределение. Владение этими действиями позволяет ученику построить образ своего «Я», способствует личностному, профессиональному, жизненному самоопределению и построению жизненных планов во временной перспективе. Эта группа УУД направлена на установление учащимся значения результатов своей деятельности для удовлетворения своих потребностей, мотивов, жизненных интересов; установление связи между целью учебной деятельности и ее мотивом — определение того, «какое значение, смысл имеет для меня учение».

Выделение морально-этического содержания событий и действий; построение системы нравственных ценностей как основания морального выбора; нравственно-этическое оценивание событий и действий с точки зрения моральных норм; ориентировка в моральной дилемме и осуществление личностного морального выбора – составляющие личностных УУД.

1. К регулятивным УУД относятся: 1) целеполагание (постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно); 2) планирование (определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий); 3) прогнозирование (предвосхищение результата и уровня усвоения, его временных характеристик); 4) контроль (сличение способа действия и его результата с заданным эталоном, с целью обнаружения отклонений и отличий от эталона); 5) коррекция (внесение необходимых дополнений и корректив в план, и способ действия в случае расхождения эталона, реального действия и его продукта); 6) оценка (выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения); 7) волевая саморегуляция, как способность к мобилизации сил и энергии, к волевому усилию в преодолению препятствий, эмоциональная устойчивость к стрессам, эффективные стратегии совладания с трудными жизненными ситуациями).
2. Общепознавательные УУД: общеучебные, логические, постановка и решение проблем.

К общеучебным УУД относятся: самостоятельное выделение и формулирование учебной цели; информационный поиск; знаково-символические действия; структурирование учебной информации и знаний; произвольное и осознанное построение устного и письменного речевого высказывания; смысловое чтение текстов различных жанров; извлечение информации в соответствии с целью чтения; рефлексия способов и условий действия, их контроль и оценка; критичность; выбор наиболее эффективных способов решения задач в зависимости от условий;

К логическим общепознавательным действиям относятся: анализ объекта с выделением существенных и несущественных признаков; синтез, как составление целого из частей, в том числе с восполнением недостающих компонентов; выбор оснований и критериев для сравнения, классификации, сериации объектов; подведение под понятие, выведение следствий; установление причинно-следственных связей; построение логической цепи рассуждения; выдвижение гипотез, их обоснование; доказательство.

Постановка и решение проблем включает: формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера.

1. Группа коммуникативных УУД включает: планирование учебного сотрудничества; постановку вопросов; построение речевых высказываний; лидерство и согласование действий с партнером.

Таблица целей обучения теме «Решение систем линейных уравнений»

(Алгебра. 7 класс. Изд. 18-е / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. – М.: Издательство «Просвещение», 2009 г.)

Формулировки обобщённых целей

Формулировки учебных задач, с помощью которых достигается обобщённая цель

Проект на тему: «Методы решения симметрических и однородных систем рациональных уравнений».

Проект разработан для дополнительной работы с детьми.

На элективном курсе мы изучаем данный материал с детьми.

Просмотр содержимого документа
«Проект на тему: «Методы решения симметрических и однородных систем рациональных уравнений».»

Проект на тему: «Методы решения симметрических и однородных систем рациональных уравнений».

Автор: Хабибова Патимат Магомедовна – учитель математики МКОУ «Ободинская СОШ»

Знакомство с темой проекта. Поиск информации и справочной литературы в библиотеке и сети Интернет. Анализ и обработка информации. Обсуждение возможных вариантов исследования, сравнение предполагаемых стратегий, выбор способов, сбор и изучение информации, составление плана работы над проектом.

Основные теоретические положения.

Методы решения систем линейных однородных уравнений.

Методы решения систем нелинейных однородных уравнений. а) Однородные системы уравнений;
б) Симметричные системы уравнений.

Цель данного проекта – глубоко изучить литературу по проблеме, с научных позиций осмыслить, обобщить, проанализировать педагогический опыт и определить пути в данном направлении. Расширить свои знания в области математики, связанные с понятием «Системы уравнений». На эти темы отдельных часов в программе не выделено, она изучается в рамках тех уроков, где рассматриваются конкретные виды уравнений: целые, дробно-рациональные, иррациональные, показательные, логарифмические, тригонометрические. Задача проекта заключается в том, что для успешной подготовки учащихся к сдаче ЕГЭ требуется умение решать различные системы уравнений, а в курсе средней школы им отведено недостаточно времени, необходимого познать этот вопрос глубже. Основная часть проекта состоит из трёх частей: основные теоретические положения темы, методы решения однородных и симметрических уравнений,опыт работы ( методы решения однородных и симметрических систем уравнений).

РАЗДЕЛ 1. 1.1 Основные теоретические положения.

Если система однородных линейных уравнений:

, то она имеет единственное решение , ;

, то она имеет ненулевые решения.

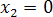
Теорема. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е. .

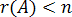
1.2 Методы решения систем линейных однородных уравнений. Метод Крамера. Пример. Решить систему .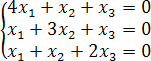

система имеет только нулевое решение .

Ответ: .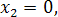

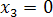
Пример. Решить систему.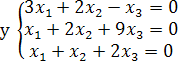

матрица системы.

Так как определитель системы 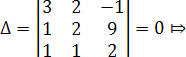система имеет отличные от нуля решения.

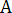
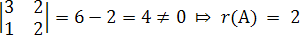
Найдем ранг матрицы . Поскольку определитель третьего порядка равен нулю, рассмотрим определитель второго порядка

.

Этот определитель является базисным.

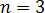
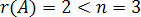
Так как и , то система имеет бесчисленное множество решений.

1. Составим систему из уравнений коэффициенты, которых вошли в базисный минор: .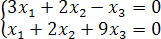

Неизвестные – главные неизвестные, неизвестное

Решаем систему методом Крамера.

Определитель системы , найдем дополнительные определители:

Итак, ; общее решение.

2. Положив получаем одно частное решение:

.

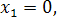
Положив получаем второе частное решение:

Положив получаем третье частное решение:

Метод Гаусса.
1. Решить систему уравнений

Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:

Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например, следует рассматривать как свободный параметр.
Далее нужно присвоить этому параметру произвольное значение и выразить базисные неизвестные , и через c.

Преобразованная матрица соответствует следующей системе уравнений:

Из последнего уравнения следует, что .
Выразим остальные базисные переменные:

Таким образом, общее решение системы найдено

1.2 МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
В этой части проекта я рассмотрю два основных метода решения систем нелинейных уравнений:
1) Однородные системы нелинейных уравнений;
2) Симметричные системы уравнений.
1) Однородные системы уравнений:
Уравнения называются однородными, если все слагаемые, содержащие неизвестные, имеют одну и ту же степень (показатели степеней разных неизвестных в слагаемых складываются). ИЛИ: Определение . Система двух уравнений с двумя неизвестными вида

называется однородной. Многочлены в левых частях уравнений системы являются однородными многочленами степени .

Пример Решить систему уравнений

Решение. Положим , тогда из первого уравнения системы находим . Но пара чисел не является решением второго уравнения системы. Поэтому рассмотрим случай, когда . Разделим обе части первого уравнения на . Получим . Это уравнение вместе со вторым уравнением данной системы образует систему, равносильную исходной. Решая данное уравнение, имеем или , т.е. или . Тогда данная система равносильна совокупности двух систем: и

Первая система этой совокупности не имеет действительных решений. Решив вторую систему совокупности, получим , тогда .

В примере рассмотрели однородную систему, в которой одно из чисел , равно . Если в однородной системе , , то надо такую систему свести к виду предыдущей (т.е. одно из чисел , равно ). Покажем это на примере.

Пример . Решить систему уравнений

Решение. Умножим первое уравнение системы на , а второе – на и сложим полученные уравнения. В результате имеем уравнение , которое вместе с первым уравнением системы образует систему, равносильную исходной. Пара чисел не является решением данной системы, значит можно перейти от последнего уравнения к следующему: . Решив его, получим или , т.е. или . Имеем совокупность двух систем: и Из первой системы получаем , . Вторая система имеет решения , .

Ответ. ; ; ; . Пример Решить систему уравнений

Решение. Первое уравнение системы однородно, но заметим, что все члены его левой части делятся на . Поэтому данную систему заменим равносильной ей совокупностью двух систем уравнений и Решая первую систему совокупности, находим , ; , . Процесс решения второй системы известен, ей удовлетворяют четыре пары чисел: Ответ. ; ; ; ; ; .

Пример . Решить систему уравнений

Решение. Пара удовлетворяет системе. Пусть . Разделим на оба уравнения системы, получим откуда находим Значит, . Положим , тогда . Заметим, что при имеем и . Решения данной системы запишем парой вида , где .

Рассмотрим примеры систем, в которых левые части уравнений являются однородными многочленами степени выше второй.

Пример . Решить систему уравнений

Решение. Разложим левые части уравнений на множители Разделим уравнения последней системы почленно, в результате получим уравнение . Полученное уравнение вместе с первым уравнением данной системы образует систему, равносильную исходной. Положим , получим , откуда , , т.е. , . Если , то из первого уравнения системы находим и поэтому . Аналогично, если , то , .

Замечание. Систему уравнений в примере можно было решить, используя прием: первое уравнение системы помножить на , второе – на и сложить. Получим уравнение , далее обе части уравнения можно разделить на . Уравнение, полученное в результате таких преобразований, и первое уравнение данной системы образуют систему, равносильную исходной. Затем решаем кубическое уравнение относительно . Однако приведенное выше решение примера, через разложение левых частей уравнений на множители и равносильных преобразований с этими уравнениями, привело к решению квадратного уравнения, решить которое проще кубического.

Оказывается, существует стандартная подстановка x = ty (y ≠ 0), которая позволяет решить систему однородных уравнений:
Пример:
Решение.
Пусть x = ty (y ≠ 0), тогда

Зная t, легко сразу найти , учитывая, что . Используя это, найдём y,а затем и х a) t =3

Решить систему уравнений:

Ни одно из уравнений системы не является однородным, однако в левой части уравнений стоят однородные функции. Применим стандартный приём, который позволяет свести систему такого вида к однородному уравнению. Умножим первое уравнение на 4, а второе на 3 и вычтем из первого уравнения второе. Имеем:

А это уравнение уже однородное. Очевидно, что пара (0; 0) является его решением, однако непосредственной подстановкой можно убедиться, что эта пара не является решением исходной системы уравнений. Значит, разделим уравнение на Получим:

Стандартная замена приводит нас к квадратному уравнению корни которого и Система распалась на две: 1)

Теорема 1. (о симметрических многочленах)

Любой симметрический многочлен от двух переменных представим в виде функции от двух основных симметрических многочленов

Другими словами, для любого симметрического многочлена f (x, y) существует такая функция двух переменных φ (u, v), что

Доказательство этого факта хотя и доступно школьнику, но далеко выходит за рамки школьного курса, поэтому мы приведём лишь примеры, которые иллюстрируют применение этой теоремы.

Функция может быть преобразована следующим образом:

Функция может быть преобразована следующим образом:

Аналогично, симметрическая функция трёх переменных определяется как функция, которая не изменяет своего значения при произвольных перестановках своих аргументов, то есть

Для симметрических многочленов трёх переменных справедлива точно такая же теорема, как и для многочленов двух переменных, а именно:

Теорема 2. (о симметрических многочленах)

Любой симметрический многочлен от трёх переменных представим в виде функции от трёх основных симметрических многочленов:

Другими словами, для любого симметрического многочлена f (x, y) существует такая функция трёх переменных θ (u, v, w), что

Применим эту теорему для упрощения систем уравнений.

Решите систему уравнений

Эта система является симметрической, поэтому делаем стандартную замену Поскольку а из второго уравнения системы следует, что то Левая часть второго уравнения перепишется так: Относительно u и v получаем систему

Перейдем к переменным x и y:

Решите систему уравнений

Эта система – симметрическая, поэтому делаем стандартную замену u = x + y, v = xy. Преобразуем левую часть первого уравнения: тогда система принимает вид:

Итак, для u получаем уравнение Вспомним теорему о рациональных корнях многочленов. Рациональные корни нашего уравнения нужно искать среди делителей числа –4. Перебирая все делители, убеждаемся, что рациональных корней у уравнения нет. Однако эта теорема и не была теоремой существования корней. Указанная теорема констатировала лишь следующее: если у многочлена с целыми коэффициентами существуют рациональные корни (но для них имеется ещё возможность НЕ существовать), то эти корни будут иметь некоторый специальный вид. Тот случай, когда рациональных корней нет, эта теорема и не описывала.

Попробуем найти корни уравнения исходной системы среди иррациональных чисел. Однако для этого придется проявить некоторую изобретательность: стандартная замена для симметрических систем здесь, очевидно не работает.

Возводя второе уравнение в куб, получим: Таким образом, по теореме Виета, и являются корнями квадратного уравнения Отсюда и Значит,

Заметим, что мы нашли один из корней уравнения

2) Системы симметричных уравнений:

Пусть , тогда система имеет вид: .
Вычтем из первого уравнения второе уравнение:

a)
По теореме, обратной теореме Виета, данная система порождает квадратное уравнение + 4m + 3 = 0, корнями которого являются x и y. В силу симметричности имеем: (1; 3); (3; 1).
b)
Из порождённого квадратного уравнения — 4n + 3 = 0 следует решения (-3; -1); (-1; -3).
Ответ: <(1; 3); (3; 1); (-3; -1); (-1; -3)>.

Пример Решить систему уравнений

Решение. Выполним алгебраическое сложение уравнений системы, предварительно помножив первое уравнение на , а второе – на . Получим уравнение, которое со вторым уравнением системы образуют систему, равносильную исходной: Как и в предыдущих примерах, первое уравнение системы можно разделить на . В результате получим уравнение четвертой степени, решение которого громоздко. Однако, решив его и реализовав план решения системы, описанный в предыдущих примерах, получим ответ. Но дана симметрическая система, а значит, с помощью введения новых неизвестных может быть преобразована к более простому виду. Покажем это. Пусть , , тогда имеем систему и т.д. Решая исходную систему любым из предложенных способов, получим ; ; ; .

Из опыта работы.
Элективный курс по математике «Уравнения, неравенства и их системы»
Составила: Хабибова Патимат Магомедовна,
учитель математики первой категории МКОУ «Ободинская СОШ» Хунзахского района РД.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Программа данного элективного курса рассчитана на 27 часов и предназначена для учащихся 11 класса. Элективный курс позволит интересующимся школьникам получить дополнительную подготовку и сдать ЕГЭ по предмету на профильном уровне. В настоящее время практика вступительных экзаменов оторвалась от школы. Нам известно насколько велики «ножницы» между требованиями школьной программы и требованиями, которые предъявляют к поступающему ВУЗ.
Курсы, которые предлагают ВУЗы учащимся, ориентируют их на экзамен лишь в данный ВУЗ. Элективный курс «Уравнения, неравенства и их системы» поможет подготовиться учащимся к поступлению в любое высшее учебное заведение, так как основной целью этого курса является знакомство учащихся с общими методами и приемами решения уравнений, неравенств и их систем.
Задачами данного элективного курса являются:

повышение уровня математического и логического мышления учащихся;

развитие навыков исследовательской деятельности,

подготовка выпускника к сдаче конкурсного экзамена по математике.

Работа элективного курса строится на принципах:

Однородное тригонометрическое уравнение – это уравнение двух видов:

a sin x + b cos x = 0 (однородное уравнение первой степени)

либо a sin 2 x + b sin x cos x + c cos 2 x = 0 (однородное уравнение второй степени).

Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:

1) разделить обе части уравнения на cos x

2) решить получившееся выражение

Пример: Решим уравнение 2 sin x – 3 cos x = 0.

Разделим обе части уравнения на cos x:

2 sin x 3 cos x 0
———— – ———— = ———
cos x cos x cos x Получаем: 2 tg x – 3 = 0, 2 tg x = 3, tg x = 3/2
x = arctg 3/2 + πn

Условие: в уравнении должно быть выражение вида a sin 2 x.
Если его нет, то уравнение решается методом разложения на множители.

1) Разделить обе части уравнения на cos 2 x

2) Ввести новую переменную z, заменяющую tg x (z = tg x)

3) Решить получившееся уравнение

Пример: Решить уравнение sin 2 x – 3 sin x cos x + 2 cos 2 x = 0.

Разделим обе части уравнения на cos 2 x:

Получаем: tg 2 x – 3 tg x + 2 = 0.

Вместо tg x введем новую переменную z и получим квадратное уравнение:

z 2 – 3z + 2 = 0. Найдем корни: z₁ = 1, z₂ = 2. Значит: либо tg x = 1, либо tg x = 2.

Сначала найдем x при tg x = 1: x = arctg 1 + πn,x = π/4 + πn.

Теперь найдем x при tg x = 2: x = arctg 2 + πn.

Однородные логарифмические уравнения.

Решить уравнение log 2 ₃ (х 2 – 3х + 4) – 3log₃ (х + 5) log₃ (х 2 – 3х + 4) – 2log 2 ₃ (х + 5) = 0

Область определения уравнения

log₃ (х + 5) = 0 при х = -4. Проверкой определяем, что данное значение х не является корнем первоначального уравнения.Следовательно можно разделить обе части уравнения на log 2 ₃ (х+5).

Получим log 2 ₃ (х 2 – 3х + 4) / log 2 ₃ (х + 5) – 3 log₃ (х 2 – 3х + 4) / log₃ (х + 5) + 2 = 0.

Пусть log₃ (х 2 – 3х + 4) / log₃ (х + 5) = t. Тогда t 2 – 3 t + 2 = 0. Корни данного уравнения 1; 2. Возвратившись к первоначальной переменной, получим совокупность двух уравнений

[log₃ (х 2 – 3х + 4) / log₃ (х + 5) = 1

[log₃ (х 2 – 3х + 4) / log₃ (х + 5) = 2. Отсюда

Выполнив потенцирование, получим

[х 2 – 3х + 4 = х + 5,

[х 2 – 3х + 4 = (х + 5) 2 ;

[х = 2 + √5, [х = -21/13. Все корни входят в область определения.

Определение. Показательные уравнения вида называются однородными.

Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на .

Пример: 2 x = 3 x Решение:Разделим обе части уравнения на

Симметрическое уравнение нечетной степени имеет корень -1.

В результате деления симметрического уравнения нечетной степени на (х + 1) получается симметрическое уравнение четной степени на единицу меньше. 3. Симметрическое уравнение четной степени 2n подстановкой
y = x +1|x может сводиться,на области действительных чисел, к уравнению степени n и к уравнениям второй степени.

1. Уравнения называются симметрическими уравнениями 3-й степени, если они имеют вид ах 3 + bx 2 + bх + a = 0.

Пример. х 3 + 2x 2 + 2х + 1 = 0. Решение.У исходного уравнения обязательно есть корень х = -1, поэтому разделим х 3 + 2x 2 + 2х + 1 на (х + 1) по схеме Горнера:

х 3 + 2x 2 + 2х + 1 = (х + 1)(x 2 + х + 1) = 0.

Квадратное уравнение x 2 + х + 1 = 0 не имеет корней.

Другой способ: Поскольку ах 3 + вх 2 + вх + а = а (х 3 + 1) + вх (х+1) = а (х+ 1) (х 2 — х+ 1) + вх (х+ 1) = (х+1) (ах 2 + (в — а) х + а), то уравнение (1) равносильно совокупности уравнений

х + 1 = 0 и ах 2 + (в — а) х + а = 0, решить которую просто.

Пример 1. Решить уравнение

3х 3 + 4х 2 + 4х + 3 = 0.

Уравнение является симметрическим уравнением третьей степени. Разложим на множители левую часть уравнения

3х 3 + 4х 2 + 4х + 3 = 3 (х 3 + 1) + 4х (х + 1) = ( х + 1) (3х 3 – 3х + 3 + 4х) = ( х+ 1) (3х 3 + х + 3).

Уравнение равносильно совокупности уравнений

х + 1 = 0 и 3х 3 + х + 3 = 0,

2. Уравнения называются симметрическими уравнениями 4-й степени, если они имеют вид ах 4 + bx 3 + сх 2 + bх + a = 0.

а) Разделить обе части исходного уравнения на х 2 . Это действие не приведет к потере корня, ведь х = 0 решением заданного уравнения не является.

б) С помощью группировки привести уравнение к виду:

а(x 2 + 1/x 2 ) + b(x + 1/x) + c = 0.

в) Ввести новую неизвестную: t = (x + 1/x).

Проделаем преобразования:t 2 = x 2 +2 + 1/x 2 . Если теперь выразить x 2 + 1/x 2 , то t 2 – 2 = x 2 + 1/x 2 .

г) Решить в новых переменных полученное квадратное уравнение:

аt 2 + bt + c – 2a = 0.

д) Сделать обратную подстановку.

6х 2 – 5х – 38 – 5/х + 6/х 2 = 0, 6(х 2 + 1/х 2 ) – 5(х + 1/х) – 38 = 0.

Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2 ) = t 2 – 2, имеем:

6t 2 – 5t – 50 = 0, t = -5/2 или t = 10/3. Вернемся к переменной х. После обратной замены решим два полученных уравнения: 1) x + 1/x = -5/2; х 2 + 5/2 х +1 = 0;

х = -2 или х = -1/2. 2) x + 1/x = 10/3; х 2 – 10/3 х + 1 = 0; х = 3 или х = 1/3. Ответ: -2; -1/2; 1/3; 3.

Способы решения некоторых видов уравнений высших степеней

1. Уравнения, которые имеют вид (х + а) n + (х + b) n = c, решаются подстановкой t = x + (a + b)/2. Этот метод называется методом симметризации.

Примером такого уравнения может быть уравнение вида (х + а) 4 + (х + b) 4 = c.

Делаем подстановку, о которой говорилось выше: t = x + (3 + 1)/2 = х + 2, после упрощения: х = t – 2, (t – 2 + 3) 4 + (t – 2 + 1) 4 = 272, (t + 1) 4 + (t – 1) 4 = 272. Убрав скобки с помощью формул, получим:t 4 + 4t 3 + 6t 2 + 4t + 1 + t 4 – 4t 3 + 6t 2 – 4t + 1 = 272, 2t 4 + 12t 2 – 270 = 0, t 4 + 6t 2 – 135 = 0, t 2 = 9 или t 2 = -15. Второе уравнение корней не дает, а вот из первого имеем t = ±3. После обратной замены получим, что х = -5 или х = 1. Ответ: -5; 1.

Для решения подобных уравнений часто оказывается эффективным и метод разложения на множители левой части уравнения.

2. Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.

Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной. Пример.(х + 1)(х + 2)(x + 3)(x + 4) = 24. Решение. Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам: ((х + 1)(x + 4))((х + 2)(x + 3)) = 24, (х 2 + 5х + 4)(х 2 + 5х + 6) = 24. Сделав замену х 2 + 5х + 4 = t, имеем уравнение t(t + 2) = 24, оно является квадратным: t 2 + 2t – 24 = 0, t = -6 или t = 4. После выполнения обратной замены, легко находим корни исходного уравнения. Ответ: -5; 0.

3. Уравнения вида (х + а)(х + b)(x + c)(x + d) = Ах 2 , где аd = cb.

Метод решения заключается в частичном раскрытии скобок, делении обеих частей на х 2 и решении совокупности квадратных уравнений.

Перемножив в левой части первые две и последние две скобки получим:

(х 2 + 14х + 24)(х 2 + 11х + 24) = 4х 2 . Делим на х 2 ≠ 0: (х + 14 + 24/х)(х + 11 + 24/х) = 4. Заменой (х + 24/х) = t приходим к квадратному уравнению: (t + 14)(t + 11) = 4; t 2 + 25х + 150 = 0. t = 10 или t = 15. Произведя обратную замену х + 24/х = 10 или х + 24/х = 15, находим корни. Ответ: (-15 ± √129)/2; -4; -6.

Данное уравнение сразу трудно классифицировать и выбрать метод решения. Поэтому сначала преобразуем, используя разность квадратов и разность кубов: ((3х + 5) 4 – 4х 2 ) + ((х + 6) 3 – 1) = 0. Затем, после вынесения общего множителя, придем к простому уравнению: (х + 5)(х 2 + 18х + 48) = 0. Ответ: -5; -9 ± √33. Задача. Составить многочлен третьей степени, у которого один корень, равный 4, имеет кратность 2 и корень, равный -2. Решение.По следствию из теоремы Безу, если у многочлена есть корень кратности 2 равный 4 и есть корень -2, то он без остатка должен поделиться на (х – 4) 2 (х + 2), значит:f(x)/((х – 4) 2 (х + 2)) = q(x) или f(x) = (х – 4) 2 (х + 2)q(x).Умножив первые две скобки, и приведя подобные слагаемые, получим: f(x) = (х 3 – 6x 2 + 32)q(х), х 3 – 6x 2 + 32 – многочлен третьей степени, следовательно, q(x) – некоторое число из R (т. е. действительное). Пусть q(x) есть единица, тогда f(x) = х 3 – 6x 2 + 32.

ЗАКЛЮЧЕНИЕ. Тема «Уравнения и системы уравнений» — одна из ключевых тем школьного курса математики. На ней основаны темы решения неравенств и текстовых задач, аналитическое решение геометрических задач. Если говорить о практическом применении, то можно сказать, что ни одна экономическая модель не обходится без этой темы. Практически все естественные науки тем или иным образом затрагивают тему решения уравнений и систем уравнений. Знание этой темы может пригодиться учащимся в их повседневных делах.
Итак, в своём проекте я, во-первых, обобщила основные методы решения систем линейных однородных уравнений с двумя переменными, во-вторых, рассмотрела некоторые методы решения систем нелинейных уравнений с двумя переменными, в-третьих, составила решебник, который, я надеюсь, поможет читающим мой проект лучше понять тему, которую я выбрала, и сформирует навык решения систем уравнений. Другими словами я решила все задачи, которые стояли передо мной, и справилась с моей целью. Надеюсь, мой проект был интересен для чтения, повторения прошлого и знакомства с частью нового материала. Во-первых анализ вступительных экзаменов по математике показывает, что задачи на однородные уравнения и системы однородных уравнений представляют для абитуриентов определенную сложность, поэтому умение их решать во многом определяет успешную сдачу экзамена в любом ВУЗе. Во-вторых в настоящее время в различных сферах проектной деятельности (технической, экономической и др.) все шире применяют компьютерные исследования на основе модели. Под моделью понимается формализованное описание объекта, системы объектов, процесса или явления, выполненное посредством математических соотношений, набора чисел, словесных формул и т. п.. Часто описание процессов или явлений сводится к их описанию посредством линейных однородных уравнений или систем однородных уравнений. Поэтому тема проектной работы является актуальной. Познавательная ценность для данной области знаний: 1. умение решать однородные уравнения и системы однородных уравнений для дальнейшего обучения в ВУЗе. 2. применение однородных уравнений и систем однородных уравнений в проектной деятельности человека.

В научно-практической работе предметом исследования являются различного вида однородные уравнения (алгебраические, показательные, логарифмические и тригонометрические) и системы однородных уравнений. Сложность математического описания любого исследуемого объекта зависит: от необходимости одновременного рассмотрения всей совокупности факторов, отражающих свойства объекта и количества взаимосвязей. Ведущая идея: изучить существующие виды разнообразных задач содержащие однородные уравнения и системы уравнений, проанализировать их решения, а также научиться их решать различными способами.

В работе рассмотрены различные подходы к решению алгебраических, показательных, логарифмических и тригонометрических однородных уравнений и систем однородных и симметрических уравнений. В результате проведенного анализа решения данных уравнений и систем уравнений был сделан вывод о том, что наиболее часто встречающимся способом является способ замены общей части текущей переменной. Информационные источники.

1. Дорофеев Г. В. Математика. Алгебра. Функции. Анализ данных. – М.: Дрофа,2001.

2. Ионин В. Л. Системы однородных уравнений. Квант, № 9, 1975.

3. Шахмейстер А. Х. Системы уравнений. – С-Пб.: ЧеРо–на–Неве, 2004.

4. А.Х.Шахмейстер: «Системы уравнений математика»
5. Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков «АЛГЕБРА. Учебник для 9 класса с углублённым изучением математики» Москва 2006 год, 5-е издание — М.:Мнемозина, 439 страница.
6. М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич «Сборник задач по алгебре 8-9 классы» Москва «Просвещение» 1994 год, 271 страница.