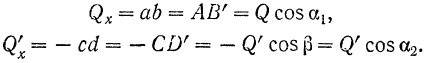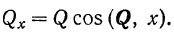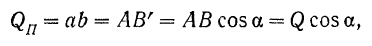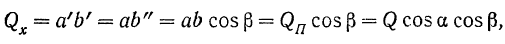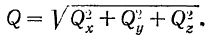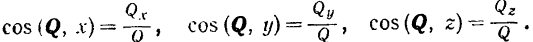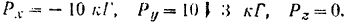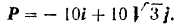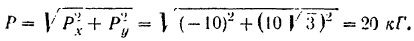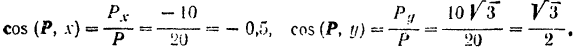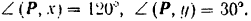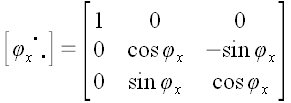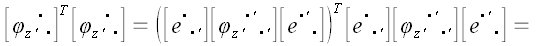Проекции вектора на ось и на плоскость
Проекции вектора на ось и на плоскость
Аналитический способ решения задач статики основан на применении метода проекции, знакомого студентам из векторной алгебры. Ввиду особой важности этого метода для дальнейшего, напомним его основы.
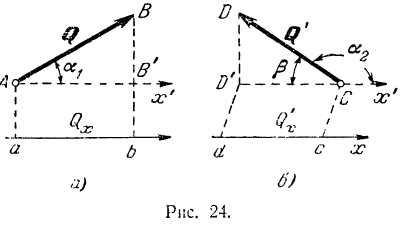
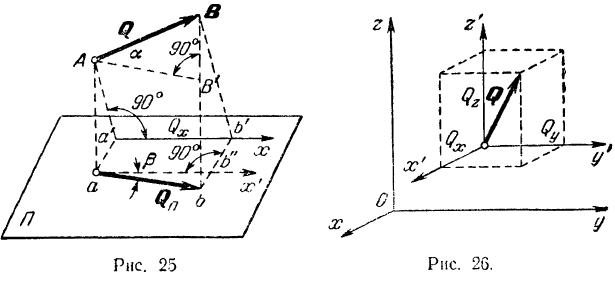
Проекцией вектора на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка оси проекций, заключенного между проекциями на нее начала и конца данного вектора (рис. 24).
Проекция считается положительной, если переход от ее начала к концу совпадает с заданным положительным
направлением оси, и отрицательной — если с противоположным.
Проекцию вектора на ось принято обозначать теми же буквами, что и вектор, но обычного шрифта, указывая нижним индексом ось проекций.
Проекции вектора на две параллельные и одинаково направленные оси равны между собой. Этим особенно удобно бывает пользоваться в тех случаях, когда вектор не лежит в одной плоскости с осью (рис. 24,(5). Из рис. 24, а и б имеем:
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между направлением вектора и положительным направлением оси проекций
Проекция будет положительной, если направление вектора составляет с положительным направлением оси острый угол, н отрицательной — если тупой.
Проекцией вектора на плоскость называется вектор, заключенный между проекциями на эту плоскость начала и конца данного вектора.
Так, например, проекцией_вектора 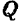
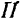
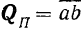
По модулю проекция вектора на плоскость:
где 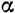
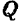
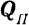
Для нахождения проекции вектора на ось, не лежащую с ним в одной плоскости, иногда бывает удобно
спроектировать сначала вектор на плоскость, в которой лежит эта ось, а затем уже проекцию вектора на плоскость спроектировать на данную ось.
Так, проекция вектора 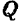
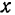
где 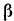
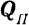
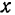
Зная проекции вектора па оси прямоугольной декартовой системы координат, легко найти и модуль и направление вектора.
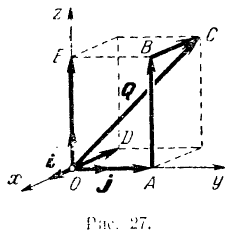
Так как модуль вектора равен диагонали прямоугольного параллелепипеда (рис. 26), ребра которого равны абсолютным значениям проекций вектора на оси координат, то модуль вектора
Модуль вектора равен квадратному корню из суммы квадратов его проекций на три любые взаимно перпендикулярные оси.
Направление вектора определяется из равенств:
Косинус угла между вектором и положительным направлением оси проекции называется направляющим косинусом. Он равен отношению проекции вектора на соответствующую ось к модулю вектора.
Заметим, что в формуле (4) надо брать арифметическое значение корня.
Вектор 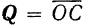
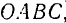
Век горы 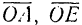
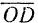
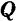
Векторы 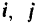
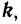
Составляющая вектора по оси координат равна проекции вектора на данную ось, умноженной на соответствующий координатный орт:
Подставляя последние выражения в предыдущее равенство. получаем весьма важную формулу разложения вектора по осям координат
где коэффициенты 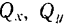
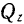
Пример задачи:
Даны проекции силы на оси прямоугольной системы координат
Написать формулу разложения заданной силы по осям координат, а также найти ее модуль и направление.
Решение:
По формуле 
Отсюда, углы между направлением силы и положительными направлениями осей координат:
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Проекция вектора на плоскость заданную уравнением
В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
.Геометрическое определение вектора
.Алгебраические операции над направленными отрезками
..Сложение направленных отрезков
..Умножение направленных отрезков на число
..Параллельное проектирование вектора в пространстве
. Проекция точки на плоскость
. Проекция вектора на плоскость
..Ортогональная проекция вектора в пространстве
. Ортогональная проекция вектора на плоскость
. Ортогональная проекция вектора на прямую и направленную ось
..Векторы в трехмерном геометрическом пространстве
..Линейная зависимость векторов и размерность пространства
..Различные формы записи векторов
..Линейные операции над векторами в координатной форме
. Свойства скалярного умножения
. Скалярное умножение в декартовых координатах
..Некоторые примеры использования скалярного умножения
..Площадь параллелограмма, построенного на векторах
..Задачи на применение определителей
..Определитель третьего порядка и его свойства
..Векторное умножение векторов базиса декартовой системы координат
.Ковариантные и контравариантные координаты вектора
..Индексная форма записи для выражений с определителями
..Свойства символов Веблена
..Операция векторного умножения в произвольных косоугольных координатах
.Линейный оператор и его матрица
..Примеры линейных операторов
.Доказательство теоремы об определителе
.Общие определения алгебраических операций с тензорами
.Примеры на применение тензоров в физике
..Задачи на тождественные преобразования
..Примеры линейных операторов
1. Оператор тождественного преобразования.
Оператор тождественного преобразования переводит любой вектор сам в себя. Другими словами, он возвращает тот же самый вектор, который принял, ничего с ним не делая. Оператор тождественного преобразования обозначается буквой I , следовательно: 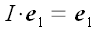
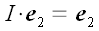
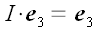
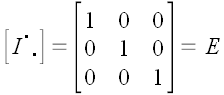
Проверим закон преобразования координат тождественного преобразования при смене координатной системы.
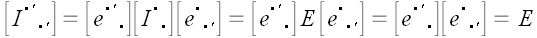
Следовательно, как, впрочем, и можно было ожидать, матрица оператора тождественного преобразования равна единичной матрице.
Умножим матрицу тождественного преобразования на матрицу координат метрического тензора.
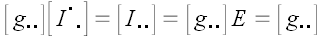
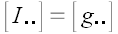
Аналогично можно показать, что
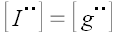
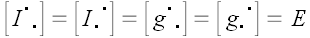
Отсюда можно сделать вывод, что матрицы тождественного преобразования и метрического тензора совпадают. Этот факт имеет простое геометрическое объяснение. Матрица метрического тензора является матрицей перехода от основной системы координат к взаимной и наоборот, но вектор, координаты которого преобразуются, остается при этом тем же самым вектором. Следует заметить, что запись координат метрического тензора со смешанными индексами, хотя и не запрещена правилами, обычно не используется. Поскольку 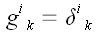
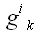
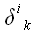
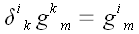
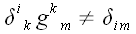
Матрицу 

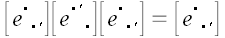
Мы видим, что матрица тождественного преобразования многолика, и может принимать вид любой невырожденной матрицы в зависимости от способа ее трактовки.
Произвольное линейное преобразование также может быть представлено координатами сразу в двух координатных системах. В самом деле, пусть 
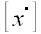
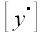
Тогда 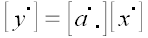
Выразим координаты вектора 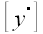
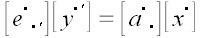
Умножим правую и левую части равенства на матрицу 
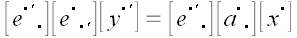
Учитывая, что 
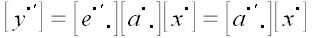
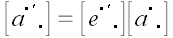
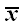
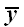
Ничего принципиально нового такая возможность не дает, и в дальнейшем мы не будем рассматривать линейные операторы, отнесенные к двум системам координат одновременно.
2. Обратный оператор
Если 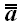
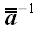
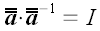
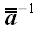
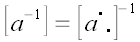
3. Оператор растяжения
Представим, что геометрическое пространство построено из эластичного материала. Растянем его в направлении оси x так, чтобы каждый отрезок, расположенный вдоль этой оси растянулся бы в λ раз. В этом случае x координата каждого вектора увеличится в λ раз, в то же время остальные его координаты останутся без изменения.

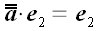
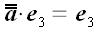
Мы не вводим специального обозначения для этого оператора.
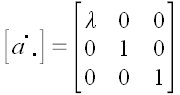
Теперь, если мы растянем наше пространство по направлениям всех трех осей, то получим оператор трехосного растяжения:
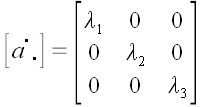
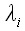
4. Оператор сдвига
Представим, что все пространство заполнено тонкими листами бумаги, аккуратно сложенными в одну стопку (рис. 50). Сдвинем листы на одну и ту же величину относительно друг друга в направлении оси y .
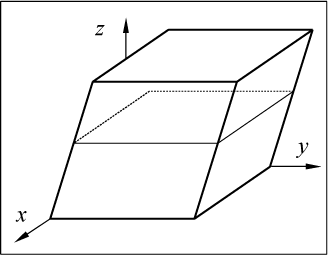
Если считать лисы бумаги очень тонкими слоями геометрического пространства, то векторы, находящиеся в этом пространстве и с ним связанные также сдвинутся. Координаты векторов параллельных плоскости xoy , как лежащие в сдвигаемых слоях, не изменятся. Зато концы вектора перпендикулярного плоскости xoy сдвинутся один относительно другого в направлении оси y на величину пропорциональную длине вектора. Общее выражение для такого преобразования в векторной форме можно записать так: 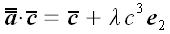
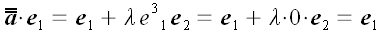
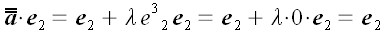
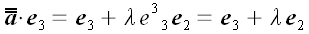
Отсюда получаем матрицу линейного преобразования сдвига:
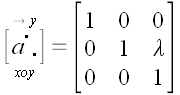
Аналогично получаем матрицу оператора сдвига в направлении оси y параллельно плоскости yoz .
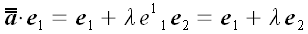
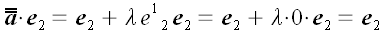
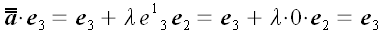
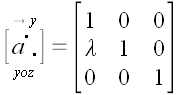
Матрицы сдвигов относительно других осей получаются точно так же.
5. Оператор поворота относительно координатной оси
Если в предыдущих случаях для вычисления матриц операторов мы могли использовать произвольную систему координат, то для вычисления матрицы оператора поворота без декартовой системы координат обойтись очень трудно. Пусть 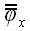
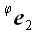
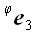
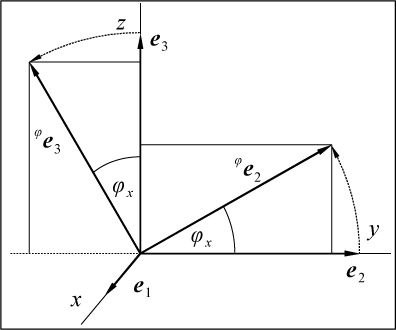
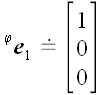
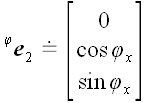
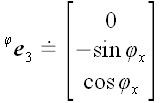
И, следовательно,
Аналогично можно доказать, что
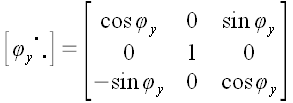
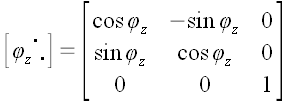
6. Оператор поворота относительно произвольной оси
Если нам необходимо выполнить преобразование поворота относительно произвольной оси, не совпадающей ни с одной из координатных осей, мы можем воспользоваться услугами вспомогательной координатной системы 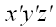
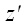
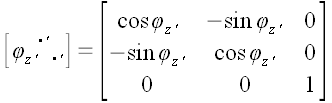
Теперь достаточно воспользоваться известным законом преобразования координат оператора, чтобы найти матрицу его координат в старой системе: 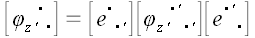
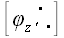
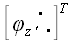
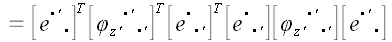
Матрица преобразования 
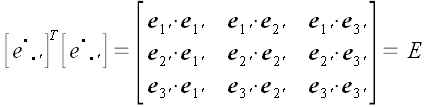
По аналогичным причинам 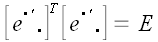
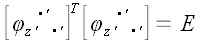
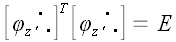
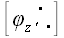
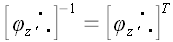
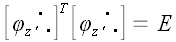
Пусть теперь 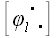
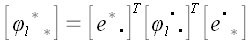
В ортонормированном базисе
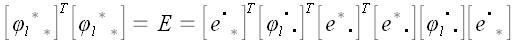
Так как 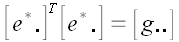
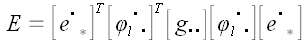
Умножим правую и левую части равенства на матрицу 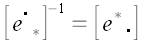
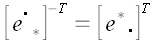
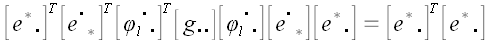
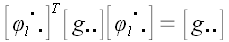
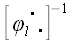
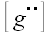
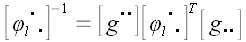
Вообще для произвольного оператора 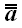
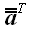
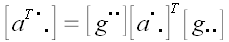
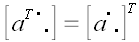
Следовательно, обратная матрица произвольного ортогонального оператора и оператора поворота в частности равна матрице сопряженного оператора.
В свое время мы отложили полное доказательство теоремы о том, что объем параллелепипеда, построенного на векторах, равен определителю, составленному из координат этих векторов. Сейчас, после проделанной нами работы, эти лучшие времена настали.
Пусть 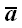
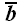
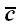
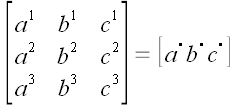
Повернем все три вектора как жесткое целое относительно оси x таким образом, чтобы вектор 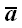
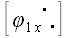
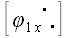
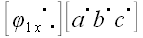
Повернем теперь все векторы относительно оси z так, чтобы вектор 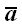
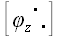
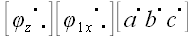
Теперь снова повернем все векторы относительно оси x так, чтобы вектор 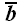
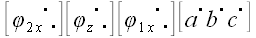
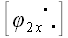
В результате этих преобразований вектор 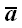
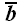
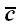
Применим теперь оператор сдвига в плоскости параллельной xoz в направлении оси x , который совместит вектор 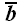
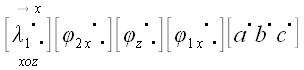
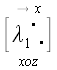
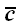
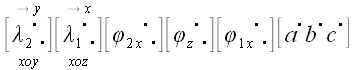
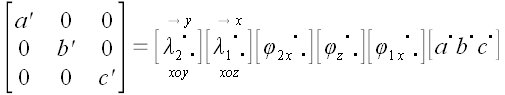
Определитель левой матрицы 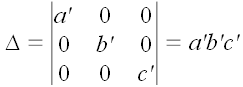
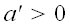
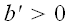
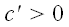
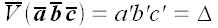
Если 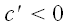
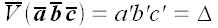
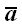
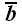
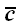
Но 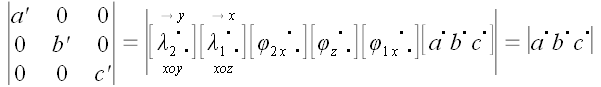
поскольку определители всех матриц, использованных операторов, равны единице! Следовательно, для любых трех некомпланарных векторов
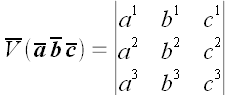
Проекции векторов на прямую и на плоскость
Проекция вектора на прямую
Пусть на плоскости задана прямая и пересекающая ее прямая . Проекцией вектора на прямую параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис.1.13,а). Если прямая перпендикулярна прямой , то проекция называется ортогональной.
Пусть в пространстве дана прямая и пересекающая ее плоскость . Проекцией вектора на прямую параллельно плоскости (вдоль плоскости ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис. 1.13,6). Если плоскость перпендикулярна прямой , то проекция называется ортогональной.
Проекция вектора на плоскость
Пусть в пространстве задана плоскость я и пересекающая ее прямая . Проекцией вектора на плоскость параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция начала , а концом — проекция конца вектора (рис. 1.14). Если прямая перпендикулярна плоскости , то проекция называется ортогональной.
Свойства проекций векторов
1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.
2. Проекции равных векторов равны.
3. Проекция суммы векторов равна сумме их проекций.
4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).
5. Проекция линейной комбинации векторов равна линейной комбинации проекций.
Рассмотрим эти свойства для проекций векторов на прямую параллельно прямой . Для проекций векторов на плоскость или на прямую параллельно плоскости доказательства аналогичные.
Докажем первое свойство. Пусть — проекция вектора на прямую вдоль прямой , а — проекция вектора на прямую вдоль той же прямой , причем прямые и параллельные (рис. 1.15). Четырехугольник, образованный пересечением пары параллельных прямых и штриховыми линиями, параллельными прямой , является параллелограммом. Следовательно, , т.е. проекции одного и того же вектора на параллельные прямые равны.
Докажем второе свойство. Пусть на плоскости даны равные векторы и , не параллельные прямой (см. рис. 1.16). Построим равные им векторы и . Из равенства следует, что четырехугольник — параллелограмм, а треугольники и равны по стороне и двум прилежащим углам
как углы с соответственно параллельными сторонами). Следовательно, , т.е. равные векторы, не параллельные прямой , имеют равные проекции. Если же векторы параллельны прямой , то их проекции также равны, как нулевые векторы. Второе свойство доказано.
Доказательство третьего свойства очевидно для векторов и (рис. 1.17): проекция вектора равна сумме проекций и , векторов и , т.е. . Для произвольных векторов и (у которых конец вектора не совпадает с началом вектора ) доказательство сводится к рассмотренному случаю для равных им векторов и , так как равные векторы имеют равные проекции (по второму свойству).
Доказательство четвертого свойства следует из теоремы Фалеса (см. разд. В.2). На рис.1.18 изображены векторы и 0)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAWBAMAAACCkIcHAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAvWZBmjHwIdCB4BFRAWKYcvQAAAFOSURBVCjPY2AgDHgm4JK5EgCmAjcwcAphSPIaX2DgXgpicS8G8vwU0BWEuQDFLUAsTgEgUSeAJs+exHCugOEWSN+1A0CC4zVYOKQApoDlLQObAwPTWiDz3AYgwfQILMwsEgBVwNHLcHEtA+tTIHPGBSBx+8UFiApBW4iCe7IMF98y8CYBmYJgATmo4eyOtjAFjE8ZeIGSvCJgAT0HqO+ue+mCaDsBBsbHYN28K0F8pmVrYc67PQPk6n1QBRcYeDtBomohj2EKuMEKQFYAfeZ4AWIF02OeJ7AAmAG24lYvA2MuxIEgrKfAuwziDXYPSJheecBwTQDsSJA3mYDa/UAGM7BCPcHA+obBzoCBNxPk3g0M9xyggQ0PBqCrlIBhwA5y2a0DDKwgsw1QgpqBXQnIZsqFRRYOcAOUVLhTcSuwgiQYnPLcrQSSHIsBESkWAKi0S8GJu/2KAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, а также их проекции и . По теореме Фалеса , следовательно, , что и требовалось доказать. В случае доказательство аналогичное.
Пятое свойство проекций следует из третьего и четвертого.
Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).
1. Если на плоскости заданы две пересекающиеся прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих проекций и на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. .
2. Если в пространстве заданы три прямые и , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор в пространстве можно однозначно представить в виде суммы своих проекций на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. .
В самом деле, пусть прямые и пересекаются в точке (рис.1.19,а). Приложим вектор к точке , т.е. рассмотрим вектор . По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство , которое равносильно доказываемому равенству , так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.
Если же вектор коллинеарен одной из прямых, например , то соответствующие проекции имеют вид: и равенство , очевидно, выполняется.
Аналогично доказывается второе утверждение.
Справедливы утверждения, обратные к указанным в теореме 1.1.
Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы и соответственно.
Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы соответственно.
В самом деле, отложим от произвольной точки векторы (рис.1.19,6). Тогда из равенства следует, что , т.е. вектор — является диагональю параллелепипеда, построенного на векторах (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому — проекции вектора на прямые (проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые). Так как равные векторы и имеют равные проекции (свойство 2), заключаем, что проекции вектора на прямые равны соответственно. Наконец, проекции на прямые равны проекциям на параллельные им прямые, содержащие векторы соответственно.
Пример 1.5. Если прямая пересекает стороны треугольника (или их продолжения) в точках соответственно, то
Решение. Найдем отношения проекций векторов на прямую вдоль прямой (рис. 1.20). Для этого через точку проведем прямую , параллельную прямой . По свойству 4 проекций имеем:
Перемножая эти пропорции, получаем , что равносильно доказываемому равенству.
Заметим, что доказанное утверждение является частью теоремы Менелая.
Пример 1.6. Если на сторонах треугольника взяты соответственно точки так, что прямые пересекаются в одной точке, то
Решение. Пусть прямые пересекаются в точке (рис.1.21). Через точку проведем прямые и параллельно и соответственно. По свойству проекций (свойство 4):
Учитывая эти равенства и свойства отношений коллинеарных векторов (см, разд.1.2.1), преобразуем левую и правую части последнего равенства:
Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:
Найдем обратное отношение , что и требовалось доказать.
Заметим, что доказанное утверждение является частью теоремы Чевы.
http://rdt45m.narod.ru/tenzor_html/tenzor2_2.htm
http://mathhelpplanet.com/static.php?p=proektsii-vektorov-na-pryamuyu-i-na-ploskost