Проекты по алгебре 8 класс квадратные уравнения

Презентация к уроку алгебры в 8 классе по теме «Решение квадратных уравнений по формуле»
презентация к уроку по алгебре (8 класс) по теме

Урок объяснения нового материала по теме «Решение квадратных уравнений по формуле» в 8 классе. УМК Ю.Н. Макарычев,Н.Г. Миндюк и др.

Скачать:

Вложение	Размер
reshenie_kvadratnyh_uravneniy_po_formule.pptx	97.41 КБ

Предварительный просмотр:

Подписи к слайдам:

Решение квадратных уравнений по формуле Цели: Вывести общую формулу для нахождения корней квадратных уравнений Формировать умения использовать данные формулы при решении квадратных уравнений.

Назовите коэффициенты квадратного уравнения х 2 — 5х+4=0; 4х- 5 х 2 — 1=0; 4 х 2 — 4х +1=0.

Решите уравнения: 2х ²-18=0 х²=7 4у²+7у=0 х²+9=0 Х²+16=0 8у²-5у=0 (х-3)²-9=0 (х+3)²-4=0

Вспомните шаги алгоритма для решения квадратного уравнения методом выделения квадрата двучлена. Решите уравнение: 2х ²-24х+54=0

Рассмотрим решение уравнений в тетраде . 2х ²+3х+1=0 ах ²+вх+с=0

D=b ²-4ac D ˃0, то уравнение имеет 2 корня D˂0 , то уранение не имеет корней D=0, то уравнение имеет 1 корень

Корни уравнения: Х=- b/2a, если D=0 Х= — b+ D 2a Х = — b- D 2a

Выполним упражнение: № 533 ( a , б,в ) №534 Как найти корни квадратного уравнения?

Вывод: Вычислить дискриминант и сравнить его с нулем. Если дискриминант больше или равен нулю найти его корни по формулам., если меньше нуля записать , что корней нет.

Домашнее задание: П.22- выучить вывод, рассмотреть примеры 1-3 №536 (любые три) Выучить формулы Составить любое своё квадратное уравнение и решить его.

Итог: От чего зависит количество корней квадратного уравнения? Сколько корней может иметь квадратное уравнение? Как найти дискриминант? Как вычислить корни?

Рефлексия: Узнал новое Понял хорошо Не понял

По теме: методические разработки, презентации и конспекты

Презентация к уроку в 8 классе «Решение неполных квадратных уравнений»

Данная презентации способствует объяснению новой темы «Решение неполных квадратных уравнений» Поурочный план.

Урок по алгебре в 8 классе. Тема: Решение квадратных уравнений по формуле.

Урок обобщения и систематизации знаний учащихся по теме «Решение квадратных уравнений по формуле».

Презентации к урокам алгебры 7 класс по теме «Линейные уравнения с одной переменной»

Презентации к трём последовательным урокам, соответствующим программе по алгебре для 7 класса , содержат как теоретический , так и практический материал, а также упражнения для устного счёта. В .

Презентация к уроку алгебры 8 класса по теме «Неполные квадратные уравнения»

Данная презентация содержит материал для актуализации знаний по теме «Квадратные уравнения», знакомству с понятием «Неполные квадратные уравнения» и отработке навыков решения этих уравнений.

Урок алгебры 8 класса по теме «Квадратные уравнения»

Тема урока «Квадратные уравнения»Цель: Обобщение темы; проверка знаний умений и навыков; активизировать работу учащихся.

Презентация к уроку. Алгебра 7 класс. «Решение систем линейных уравнений методом подстановки»

урок открытия нового материала.

Презентация к уроку алгебры «Решение задач с помощью квадратных уравнений»

Презентация к уроку алгебры в 8 классе на тему: «Решение задач с помощью квадратных уравнений&quot.

Исследовательская работа по алгебре 8 класс «Различные способы решения квадратных уравнений»

Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание всё более полным и совершенным.

Уравнения – язык алгебры, квадратные уравнения – это фундамент, на котором построено величественное здание алгебры. Изученные способы решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных.

Просмотр содержимого документа
«Исследовательская работа по алгебре 8 класс «Различные способы решения квадратных уравнений»»

Нестандартные способы решения квадратных уравнений

Глава 1.Квадратные уравнения: из древности до наших дней 4

Глава 2. Тезаурус по теме.

2.1. Определение квадратного уравнения и его виды 8

2.2. Решение квадратного уравнения общеизвестными способами 9

Глава 3. Способы решения квадратных уравнений, отличные от традиционных

3.1. Метод выделения полного квадрата

3.2. Решения уравнений способом «переброски». 12

3.3. Учёт свойств коэффициентов квадратного уравнения…………………. 13

3.4. Решение квадратного уравнения графическим способом………………. 15

3.5. Решение квадратных уравнений с помощью циркуля и линейки………. 16

3.6. Решение квадратных уравнений с помощью номограммы………………..18

3.7. Геометрический способ решения квадратных уравнений…………………19

3.8.Решение уравнений с использованием теоремы Безу……………. 20

Глава 4.Разработка буклета памятки………………….…………………………..22

Нестандартные способы решения квадратных уравнений

Сегодня все пространство окружающее современного человека связано с математикой. А постоянные открытия в физике, технике и информационных технологиях говорят о том, что этот процесс постоянно растет . Поэтому решение многих практических задач сводится к различным уравнениям, и очень часто эти уравнения являются квадратными.

В школьном курсе рассматривается несколько типов квадратных уравнений, и способы их решения по формулам. Вместе с тем, современные научно—методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.

Выбор способа должен оставаться за учащимися. Каждый ученик должен уметь верно и главное рационально решать квадратные уравнения. Так как в некоторых случаях можно решать их устно, только для этого необходимо помнить алгоритм решения квадратных уравнений, который может пригодиться во время экзаменов (ОГЭ и ЕГЭ, учитывая ограниченность экзамена во времени), при поступлении в ВУЗы и различных жизненных ситуациях.

Таким образом, возникает необходимость изучения этих дополнительных способов решения. Все сказанное выше определяет актуальность проблемы выполненной работы.

Целью работы является выявление способов решения уравнений второй степени, отличных от изучаемых в школьной программе и оценка их с точки зрения удобства применения.

1)Познакомиться с историческими фактами, связанными с данным вопросом.

2)Описать технологии различных существующих способов решения уравнений второй степени.

3)Провести анализ этих способов, сравнить их.

4)Привести примеры применения различных способов решения уравнений.

5)Составить буклет-памятку со всеми изученными способами решения квадратных уравнений.

Объект исследования: уравнения второй степени.

Предмет исследования: способы решения уравнений второй степени.

ГЛАВА 1. Квадратные уравнения: из древности до наших дней

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000лет до нашей эры вавилоняне.

Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, как неполных, так и, полные квадратные уравнения. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VIIв.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме.В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XIIв. Бхаскары.

Обезьянок резвых стая

Власть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась,

А двенадцать по лианам

Стали прыгать, повисая.

Сколько ж было обезьянок

Ты скажи мне, в этой стае?

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

«Квадраты равны числу», т. е. ax 2 =c (5x 2 =80).

«Квадраты и числа равны корням», т. е. ax 2 +c=bx (х 2 + 10х=39).

«Квадраты и корни равны числу», т. е. ax 2 +bx=c (x 2 +21=10x).

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVIIв., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17вв. и частично 18.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 +bх=с, при всевозможных комбинациях знаков коэффициентов b, c , было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых вXVIв. учитывают, помимо положительных, и отрицательные корни. Лишь вXVIIв. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была сформулирована им впервые в 1591г.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета ещё далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

Глава 2. Тезаурус по теме.

2.1. Определение квадратного уравнения и его виды.

1) Алгоритм – точное предписание (правило) о выполнении в определенном порядке указанных операций (шагов алгоритма), позволяющее решать все задачи определенного вида.

2) Квадратным уравнением называют уравнения вида:

а – первый или старший коэффициент;

b – второй коэффициент или коэффициент при х;

с – свободный член.

3) Квадратное уравнение называют приведенным, если старший коэффициент равен 1;квадратное уравнение называют непереведенным, если старший коэффициент отличается от 1.

4)Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трехчлен обращается в нуль.

5) Решить квадратное уравнение – значит найти все его корни или установить, что корней нет.

2.2. Решение квадратного уравнения общеизвестными способами.

Разложение левой части уравнения на множители.

Разложение на множители уравнения – это процесс нахождения таких членов или выражений, которые, будучи перемноженными, приводят к начальному уравнению.

Решим уравнение х 2 +10х-24=0.

Разложим левую часть уравнения на множители:

Х 2 +10х-24=х 2 +12х-2х-24=х(х+12)-2(х+12)=(х+12)(х-2).

Следовательно, уравнение можно переписать так:

Так как произведение равно нулю, то по крайней мере один из множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х=2,а уравнение х 2 +10х-24=0.

Решение квадратного уравнений по формуле

Умножим обе части уравнения ax 2 +bx+c=0 , а ≠ 0, на 4а и, следовательно, имеем :

4а 2 х 2 +4аbc+4ac=0

((2ax) 2 +2ax ∙ b + b 2 )-b 2 +4ac=0

2ax+b = ±

2ax =-b ±

X_1,2=

Выражение b 2 — 4 ac называют дискриминантом и обозначают D, причем

Если D0, то уравнение ax 2 +bx+c=0 имеет два различных корня;

Если D=0, то два одинаковых корня;

Решение уравнений с использование теоремы Виета (прямой и обратной)

1)Как известно, приведенное квадратное уравнение имеет вид:

Его корни удовлетворяют теореме Виета, которая при а=1 имеет вид

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

А) Если свободный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.

Если p0, то оба корня отрицательные, если p

х 2 -3x+2=0; x₁ = 2 b x₂=1, так как q = 20 и q = 2 0 и p = – 3

х 2 +8х + 7 = 0; х₁ = – 7 и х₂ = – 1, так как q = 7 0 и p = 8 0.

Б) Если свободный член q приведенного уравнения (1) отрицателен (q 0. Например, х 2 + 4х – 5 = 0; х₁ = – 5 и х₂ = 1, так как q = – 5 0; х 2 – 8х – 9 = 0; х₁ = 9 и х₂ = – 1, так как q = – 90.

2) Теорема Виета для квадратного уравнения ax 2 +bx+c=0 имеет вид :

х₁х₂ = ,

х₁+х₂ = — .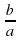

Справедлива теорема, обратная теореме Виета:

Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.

Решить уравнение x 2 -9x+14=0

Попробуем найти два числа х₁ и х₂, такие, что

Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.

Решить уравнение : x 2 +3x-28

Попробуем найти два числа х₁ и х₂ , такие, что

Нетрудно заметить, что такими числами будут — 7 и 4. Они и являются корнями данного уравнения.

Глава 3. Способы решения квадратных уравнений, отличные от традиционных

3.1. Метод выделения полного квадрата

Решим уравнение х 2 + 6х — 7 = 0

Выделим в левой части полный квадрат. Для этого запишем выражение х 2 + 6х в следующем виде: х 2 + 6х = х 2 + 2 • х • 3 .

В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х и 3. Поэтому, чтобы получить полный квадрат, нужно прибавить 3 2 , т.к.

Преобразуем теперь левую часть уравнения

прибавляя к ней и вычитая 3 2 . Имеем:

х 2 +6х-7=х 2 +2• х • 3 +3 2 — 3 2 -7= (х+3) 2 — 9 -7= (х+3) 2 -16.

Таким образом, данное уравнение можно записать так:

(х+ 3) 2 -16 = 0, т.е. (х+ 3) 2 = 1б.

Следовательно, х + 3 = 4, х ₁= 1, или х +3 = -4 , х₂ = — 7.

3.2 Решение уравнений способом «переброски»

Рассмотрим квадратное уравнение

ах 2 +Ьх+ с= 0, а ≠ 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + аЬх + ас = 0.

Пусть ах = у, откуда х = 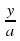; тогда приходим к уравнению

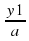
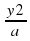
равносильному данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета. Окончательно получим х₁ = и х₂ = . При этом способе коэффициент а умножается на свободный член, как 6ы «перебрасывается» к нему, поэтому его и называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

2х 2 — 11х + 15 = 0.

«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

Согласно теореме у₁ = 6 х₁ = х₁ = 3

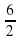
У₂ = 5 х₂ = х₂ = 2,5

3.3. Учёт свойств коэффициентов квадратного уравнения

А. Пусть дано квадратное уравнение

ах 2 + Ьх + с = 0,а≠0.

1. Если, а + Ь + с = 0 (т.е. сумма коэффициентов равна нулю), то

х₁=1, х₂= .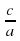

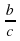
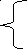
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведённое квадратное уравнение: х 2 + х + = 0.

Согласно теореме Виета x₁ + x₂ = —

x₁x₂ =

По условию, а + Ь + с = 0, откуда Ь = — a — с. Значит,

x₁ + x₂ = — = 1 +

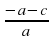
x₁x₂ = 1 •

Получаем x₁ = 1, x₂ = , что и требовалось доказать.

2. Если, a — b + c = 0, или b = a + c, то x₁ = — 1, x₂ = — .

Доказательство. По теореме Виета

x₁ + x₂ = —

x₁x₂ =

По условию, a — b + c = 0, откуда b = a + c . Таким образом,

x_{1 +} x₂ = — = -1 —

т.е. х₁ = -1 и х₂ = 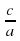, что и требовалось доказать.

1.Решим уравнение 345х 2 —137х — 208 = 0.

Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то х₁ = 1, х₂ = = .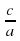

2. Решим уравнение 132x 2 + 247x + 115 = 0

Решение. Т.к. a – b + c = 0 (132 — 247 + 115 = 0 ), то x₁ = -1, x₂ = —

Б. Если второй коэффициент b = 2k – четное число, то формулу корней

X_1,2 = 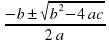можно записать в виде х_1,2 =

Решим уравнение 3x 2 – 14x + 16 = 0

Решение. Имеем : a = 3, b = — 14, c = 16, k = — 7;

D=k 2 – ac = (-7) 2 – 3 • 16 = 49 -48 =1, D 0 , два различных корня ;

В. Приведенное уравнение х 2 + px + q = 0

Совпадает с уравнением общего вида, в котором a=1, p и c = q. Поэтому для приведенного квадратного уравнения формула корней

X_1,2 =

принимает вид: x_1,2 = , или x_1,2 = — 2 – q. (2).

Формулу (2) особенно удобно использовать, когда p – чётное число.

1. Решим уравнение х 2 – 14х – 15 = 0.

Решение. Имеем: х_1,2 = 7 ± = 7 ± = 7 ± 8

3.4. Решение квадратного уравнения графическим способом

Если в уравнении : х 2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х 2 = — px – q.

Построим графики зависимости у = х2 и у = — px — q.

График первой зависимости – парабола, проходящая через начало координат.

График второй зависимости – прямая.

Возможны следующие случаи :

-прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

— прямая и парабола могут качаться (только одна общая точка), т.е. уравнение имеет одно решение;

-прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Решим графически уравнение : х 2 — 3х — 4 = 0

Решение. Запишем уравнение в виде : х 2 = 3х + 4.

Построим параболу у = х 2 и прямую у = 3х + 4.

Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13).

Прямая и парабола пересекаются в двух точках А и В с абсциссами х₁ = -1 и х₂ = 4.

3.5. Решение квадратных уравнений с помощью циркуля и линейки

Графический способ решения квадратных уравнений с помощью параболы не всегда удобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точность получаемых результатов невелика. Существует способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки.

Допустим, что искомая окружность пересекает ось абсцисс в точках В(х₁; 0 ) и D (х₂; 0), где х₁ и х₂ — корни уравнения ах 2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х₁х₂/ 1 = c/a.

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS SK, или R a + c/2a), окружность пересекает ось Ох в двух точках В (х₁; 0) и D(х₂; 0), где х₁ и х₂ — корни квадратного уравнения ах 2 + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох в точке В (х₁; 0), где х₁ — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.

Решим уравнение х 2 — 2х — 3 = 0

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).

3.6. Решение квадратных уравнений с помощью номограмм

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициент там определить корни уравнения.

Криволинейная шкала номограммы построена по формулам

Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

Если дано полное квадратное уравнение, то его надо привести к приведенному квадратному уравнению z 2 + pz + q = 0

Затем второй коэффициент и свободный член из уравнения отметить на соответствующих осях p и q, полученные точки соединить прямой.

Прямая пересекает кривую шкалу в двух точках – корнях данного уравнения, если корни положительные.

Если уравнение имеет корни разного знака, то прямая пересечет кривую шкалу в одной точке – это положительный корень. Отрицательный корень находят, вычитая положительный корень из –p.

Если же корни отрицательные, то по номограмме находят два положительных корня t₁ и t₂ для уравнения z 2 – pz + q = 0, а для уравнения z 2 + pz + q = 0 корнями будут z₁ = -t₁, z₂ = -t₂

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z₁ = 8,0 и z₂ = 1,0

2) Решим с помощью номограммы уравнение 2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение:

Номограмма дает корни z₁ = 4 и z₂ = 0,5.

3) Для уравнения z 2 — 25z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t 2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t₁ = 0,6 и t₂ = 4,4, откуда z₁ = 5t₁ = 3,0 и z₂ = 5t₂ = 22,0.

3.7. Геометрический способ решения квадратных уравнений

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми. Уравнение х 2 + 10х = 39

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39».

Строим квадрат со стороной х и на его сторонах – четыре прямоугольника высотой . В углах фигуры построим четыре квадрата со стороной . В углах фигуры построим четыре квадрата .

Подсчитаем площадь получившегося большого квадрата:

X 2 + 4 • • ( ) 2 = x 2 + 10x + ( ) 2 • 4

По условию x 2 + 10x = 39, т.е. площадь большого квадрата равна

39 + ( ) 2 • 4 = 39 + + 25 =64.

Значит, его сторона равна 8, тогда x + 2 • ( ) = 8, x = 3 (Ал–Хорезми не признавал отрицательных чисел)

А вот, например, как древние греки решали уравнение y 2 + 6y – 16 = 0

Решение представлено на рис., где у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8.

3.8. Решение уравнений с использованием теоремы Безу

Теорема Безу. Если уравнение a₀x n + a₁x n -1 … + a_n_-1x + a_n = 0, где все коэффициенты целые, имеет целые корни, то это делители свободный член.

Следствие 2: Если b является корнем многочлена f (x), то этот многочлен делится на (x-b) без остатка.

Теорема Безу даёт возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на единицу меньше.

Таким образом, один корень найден и далее находятся уже корни многочлена, степень которого на единицу меньше степени исходного многочлена. Иногда этим приёмом – он называется понижением степени – можно найти все корни заданного многочлена.

Решить квадратное уравнение: х 2 – 4х + 3 = 0

Делители свободного члена ±1, ±3.

Проверим 1, подставив в уравнение 1 – 4 + 3 = 0. Значит 1 – это корень данного уравнения. Тогда квадратный трёхчлен х 2 — 4х + 3 делится нацело на (х-1).

Разделим f(x) на (x-1), получим:

Х 2 – 4х + 3 = (х-1)(х-3)

В ходе выполнения работы с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме. Проанализировав все новые способы решения квадратных уравнений, стало очевидным, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Некоторые ( такие как, решение с использованием теоремы Безу и решение с помощью циркуля и линейки) удобно применять, когда коэффициенты невелики, другие – допускают большие коэффициенты ( например, учёт коэффициентов): графический не всегда точен, а геометрический понятен, но громоздок. Можно сделать вывод , что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения.

Составление буклета-памятки, обобщить способы решения квадратных уравнений, которые не изучают в школе. Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ОГЭ и ЕГЭ.

Данные буклеты я раздам одноклассникам и ученикам других классов. Они могут воспользоваться собранными в буклет-памятку материалами для изучения и закрепления рациональных способов решения квадратных уравнений. В дальнейшем я планирую провести опрос, насколько интересна информация, предложенная в буклете, и используют ли они данные способы для решения квадратных уравнений, если да, то какой способ они считают наиболее простым и понятным.

1.Брадис В.М. Четырёхзначные математические таблицы для средней школы.

Изд. 57-е. – М., Просвещение, 1990. С. 83.

2.Окунев А.К. Квадратные функции, уравнения и неравенства. Пособие для учителя. – М., Просвещение, 1972.

3.Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72. С. 34.

4.Соломник В.С., Милов П.И. Сборник задач по алгебре и элементарными функциям. Пособие для учителя. Изд. 2-е. – М., Просвещение, 1970.

Проект по математике на тему «Квадратные уравнения» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МБОУ – СОШ «Рязанские сады»

Проект по математике

решения квадратных уравнений»

Выполнила: ученица 8 класса

Фомина Екатерина Петровна

Руководитель: учитель математики

I квалификационной категории

Ярославцева Людмила Егоровна

История возникновения и развития квадратных уравнений………………..5

Что такое квадратное уравнение………………………………………………8

Способы решения квадратных уравнений……………………………………9

Разложение левой части уравнения на множители…………………………..9

Выделение квадрата двучлена…………………………………………………9

Решение квадратных уравнений по формуле………………………………..11

Решение квадратных уравнений с помощью теоремы Виета………………13

Свойства коэффициентов квадратного уравнения…………………………..16

Графический способ решений квадратных уравнений………………………17

Решение квадратных уравнений с помощью номограммы………………….20

Список используемых источников и литературы…………………………….24

В школе на уроках математики мы изучили несколько способов решения квадратного уравнения. От учителя я узнала, что существуют и другие способы, но мы не рассматриваем их в школьной программе. Меня это заинтересовало, и я решила узнать, какие еще способы решения квадратного уравнения существуют и сколько их всего.

Познакомиться с биографией великих математиков, занимавшихся решением квадратных уравнений.

Найти различные способы решений квадратных уравнений.

Практическое применение способов решения квадратных уравнений в современной жизни.

Найти исторический материал решений квадратных уравнений.

Систематизировать знания о различных способах решения квадратных уравнений.

Подготовить презентацию своего проекта.

Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решать три-четыре задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.

У.У. Сойер (английский математик XX века)

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.

Решение квадратных уравнений – одна из важнейших тем курса алгебры 8 класса.

В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать данные уравнения.

Часто первый избранный способ бывает далеко не самым удачным, поэтому задача каждого ученика — научиться находить не только верные, но и наиболее рациональные способы решения квадратного уравнения. В некоторых случаях их можно решать и устно, только для этого необходимо помнить алгоритм, который может пригодиться как на экзамене, так и в различных жизненных ситуациях.

Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра? Какие есть еще способы решения квадратных уравнений, и сколько их? Ответа на эти вопросы я не нашла на страницах школьного учебника. Чтобы разобраться и глубже изучить данную тему, я решила провести исследование.

Изучением квадратных уравнений люди занимались еще с древних веков. Мне захотелось узнать историю развития квадратных уравнений.

В школьных учебниках дана не полная информация о квадратных уравнениях и способах их решения.

Объект исследования: квадратные уравнения.

Предмет исследования: способы решения квадратного уравнения.

Работа с учебной и научно-популярной литературой, интернет-рессурсами.

Наблюдение, сравнение, анализ.

Ожидаемые результаты: в ходе изучения данной работы я реально смогу оценить свой интеллектуальный потенциал, расширить свой кругозор, заинтересоваться математикой и историей ее развития и, соответственно, в будущем определиться с выбором профессии. Я смогу создать проектный продукт по исследуемой теме в форме компьютерной презентации, что позволит мне компенсировать недостаточность знаний по этому вопросу.

Считаю свою работу перспективной, так как в дальнейшем этим материалом могут воспользоваться и ученики для повышения математической грамотности, и учителя на факультативных занятиях.

История возникновения и развития квадратных уравнений

Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет.

Г.В. Лейбниц (немецкий математик XVII-XVIII веков)

Уже примерно за 2000 лет до нашей эры Вавилоняне знали, как решать квадратные уравнения. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.

Найденные древние вавилонские глиняные таблички (около 2 тысяч лет до н.э.) являются самыми ранними свидетельствами об изучении квадратных уравнений. На них изложены методы решения некоторых типов квадратных уравнений. Правило решения этих уравнений совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Квадратные уравнения решали и в Индии. Древнеиндийский математик Баудхаяма в VIII столетии до н.э. впервые использовал квадратные уравнения в форме ax 2 = c и ax 2 + bx = c и привел методы их решения.

Задачи на квадратные уравнения встречаются в астрономическом трактате «Ариабхаттиам», составленном в 499 году индийским математиком и астрономом Ариабхаттой.

Другой индийский ученый, Брахмагупта (VII век), изложил общее правило решения квадратных уравнений, приведенных к единой конической форме:

ах 2 + bx = c , где a > 0 . В этом уравнении коэффициенты (кроме а) могут быть и отрицательными. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В его книгах «Арифметика» нет систематического изложения алгебры, однако в них содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений различных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Основоположником алгебры считают среднеазиатского математика Мухаммед бен Муса аль — Хорезми (787 – 850 г. г.).

Аль-Хорезми — не фамилия, это своеобразное прозвище, означающее, что Мухаммед, сын Мусы, происходит из Хорезма. (Хорезм — это крупный оазис в низовьях Амударьи, был заселён людьми в глубочайшей древности, там ещё в I тысячелетии до нашей эры существовала высокая культура). В VIII веке арабы завоевали Хорезм и уничтожили эту древнюю культуру.

Об Аль-Хорезми известно лишь, что он написал ряд трудов по астрономии и географии. И самое главное — он написал сочинение, которое по-арабски называется «Китаб аль-джебр валь-мухабала», что в переводе на русский язык означает «Книга о восстановлении и противопоставлении». Это сочинение оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки — алгебра.

Аль-Хорезми в своем алгебраическом трактате дает классификацию линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т.е. а = b х.

2) «Квадраты равны числу», т.е. а = с.

3) «Корни равны числу», т.е. вх = с.

4) «Квадраты и числа равны корням», т.е. а + с = b х.

5) «Квадраты и корни равны числу», т.е. а + bx = с.

6) «Корни и числа равны квадратам», т.е. bx + с = а.

Аль-Хорезми избегает употреблений отрицательных чисел, поэтому члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи. Он первый в Европе подошел к введению отрицательных чисел.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х 2 + bx = с , при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в 1544 г. немецким математиком М. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жиррара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Декарт Жирар Ньютон Никколо Тарталья

Франсуа Виет (1540-1603) первым догадался обозначать буквами не только неизвестные, но и коэффициенты при них. Это скромное, казалось бы, новшество внесло огромный вклад в развитие математики. Ведь если не использовать букв для обозначения коэффициентов квадратного уравнения, то записать даже несложную формулу для его решения будет довольно трудно. Недаром Виета часто называют «отцом алгебры».

Что такое квадратное уравнение?

Квадратное уравнение – это алгебраическое уравнение вида ax 2 + bx + c = 0, где х – переменная ; коэффициенты а, b и с – любые действительные числа, причем, а ≠ 0 .

Квадратные уравнения бывают трёх видов:

1. Полные квадратные уравнения (ax 2 + bx + c = 0, где) .

2. Неполные квадратные уравнения – это уравнение вида

3. Приведенные квадратные уравнения – это уравнения вида x 2 + px + q = 0 , в котором старший коэффициент a=1, р – коэффициент при х (p= ) , q – свободный член ( q = ).

Способы решений квадратных уравнений.

способ: разложение левой части уравнения на множители.

Этот метод не всегда удобен, т.к. не всегда удается применить способ группировки .

способ: выделение квадрата двучлена.

Цель метода — привести уравнение общего вида к неполному квадратному уравнению. В этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности:

Рассмотрим примеры решения полных квадратных уравнений, т. е. таких уравнений, у которых все три коэффициента отличны от нуля. Начнём с уравнений, в которых первый коэффициент равен единице. Такие уравнения называют приведёнными квадратными уравнениями.

Решим приведённое квадратное уравнение

Представим левую часть уравнения в виде квадрата двучлена. Получим:

Решим еще одно приведенное квадратное уравнение:

Если к разности х 2 — 6х прибавить число 9, то получим выражение, которое можно записать в виде (х — 3) 2 , т. е. в виде квадрата двучлена. Прибавим к левой части число 9, а чтобы равенство не нарушилось, вычтем 9 из левой части.

x – 3 = -4 или х – 3 = 4

Пример3: рассмотрим общий случай – не приведенное квадратное уравнение

Этот метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Чаще всего используется для доказательства формулы корней квадратного уравнения.

c пособ: решение квадратных уравнений по формуле.

Решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям. Поэтому поступают иначе. Решают упавнение в общем виде и в результате получают формулу корней. Затем эту формулу применяют при решении любого квадратного уравнения.

Решим квадратное уравнение:

Разделив обе его части на а, получим равносильное ему приведённое квадратное уравнение:

Преобразуем это уравнение:

Получившееся уравнение равносильно начальному. Число его корней зависит от знака дроби . Так как а ≠ 0, то 4а 2 — положительное число, поэтому знак этой дроби определяется знаком её числителя, т. е. выражения b 2 — 4ас.

Это выражение называют дискриминантом квадратного уравнения ах 2 +вх+с=0

( «дискриминант» по-латыни — различитель).

Рассмотрим теперь различные возможные случаи в зависимости от D .

источники:

http://multiurok.ru/index.php/files/issliedovatiel-skaia-rabota-po-alghiebrie-8-klass-.html

http://infourok.ru/proekt-po-matematike-na-temu-kvadratnie-uravneniya-klass-3309990.html