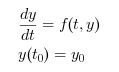Программа решение обыкновенных дифференциальных уравнений

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Программа решение обыкновенных дифференциальных уравнений

программа решения обыкновенных дифференциальных уравнений

Последовательность вызова

Аргументы

вектор или матрица вещественных значений, начальные условия.

вещественный скаляр, начальное время.

вещественный вектор, моменты времени для которых находится решение.

внешняя функция (функция, строка или список), правая сторона дифференциального уравнения.

строка, тип используемой программы решения. Имеются следующие типы программ решения: «adams» , «stiff» , «rk» , «rkf» , «fix» , «discrete» , «roots» .

вещественная константа либо вещественный вектор того же размера, что и y , относительный допуск.

вещественная константа либо вещественный вектор того же размера, что и y , абсолютный допуск.

внешняя функция (функция, строка или список), якобиан функции f .

вещественные векторы (ВХОДНЫЕ/ВЫХОДНЫЕ).

внешняя функция (функция, символьная строка или список).

целое число (начальное время).

вещественный вектор или матрица (ВЫХОДНАЯ).

вещественный вектор (ВЫХОДНОЙ).

Описание

ode решает явные обыкновенные дифференциальные уравнения, определённые как:

Это интерфейс для различных программ решения, в частности для ODEPACK.

В данной справке описывается использование ode для стандартных явных систем ОДУ.

Самый простой способ вызова ode : y = ode ( y0 , t0 , t , f ) , где y0 — вектор начальных условий, t0 — начальное время, t — вектор моментов времени, для которых вычисляется решение y и y — матрица векторов решения y=[y(t(1)),y(t(2)). ] .

Входной аргумент f определяет правую сторону дифференциального уравнения первого порядка. Этот аргумент является функцией с определённым заголовком.

Если f является Scilab-функцией, то её последовательность вызова должна быть:

где t — вещественный скаляр (время), а y — вещественный вектор (состояние) и ydot — вещественный вектор (производная первого порядка dy/dt).

Если f — строка, то это — имя компилированной процедуры Fortran или функции C. Например, если вызывается ode ( y0 , t0 , t , » fex » ) , то вызывается подпрограмма fex .

Процедура Fortran должна иметь заголовок:

где n — целое число, t — скаляр двойной точности, y и ydot — векторы двойной точности.

Функция C должна иметь заголовок:

где t — время, y — состояние, а ydot — производная состояния (dy/dt).

Эта внешняя функция может быть собрана способом, независящим от ОС, используя ilib_for_link и динамически связана с Scilab с помощью функции link.

Может случиться, что симулятору f потребуются дополнительные аргументы. В этом случае можно использовать следующую возможность. Аргумент f может также быть списком lst=list(simuf,u1,u2. un) , где simuf является Scilab-функцией с синтаксисом: ydot = f(t,y,u1,u2. un) , а u1 , u2 , . un — дополнительные аргументы, автоматически передаваемые симулятору simuf .

Функция f может возвращать вместо вектора матрицу p x q . С этой матричной нотацией решается система n=p+q ОДУ dY/dt=F(t,Y) , где Y — матрица p x q . Затем начальные условия, Y0 , должны быть так же матрицей p x q , а результат ode — матрицей p x q(T+1) [Y(t_0),Y(t_1). Y(t_T)] .

Допуски rtol и atol являются порогами для относительной и абсолютной оценённых ошибок. Оценённая ошибка y(i) равна: rtol(i)*abs(y(i))+atol(i) и интегрирование выполняется пока эта ошибка мала для каждого из элементов состояния. Если rtol и/или atol является константой, то rtol(i) и/или atol(i) являются набором констант. Значения по умолчанию для rtol и atol соответственно равны rtol=1.d-5 и atol=1.d-7 для большинства программ решения, а для «rfk» и «fix» rtol=1.d-3 и atol=1.d-4 .

Для жёстких задач лучше указывать якобиан функции правой стороны в качестве необязательного аргумента jac . Якобиан является внешней функцией, т. е. функцией со специальным синтаксисом, либо именем процедуры Fortran или функции C (символьная строка) с определённой последовательностью вызова, либо списком.

Если jac является функцией, то синтаксис должен быть J=jac(t,y) , где t — вещественный скаляр (время), а y — вещественный вектор (состояние). Результирующая матрица J должна вычислять df/dx, т. е. J(k,i) = dfk/dxi , где fk — k -тый элемент f .

Если jac является символьной строкой, то она ссылается на имя процедуры Fortran или функции C.

Процедура Fortran должна иметь заголовок:

Функция C должна иметь заголовок:

В большинстве случаев не нужно ссылаться на ml , mu и nrpd .

Если jac является списком, то для f применяются те же договорённости.

Необязательные аргументы w и iw являются векторами для хранения информации, возвращаемой подпрограммой интегрирования (см. ode_optional_output). Когда эти векторы указываются с правой стороны ode , интегрирование начинается заново с теми же параметрами, что и до остановки.

Программам решения ODEPACK можно передать больше опций с помощью переменной %ODEOPTIONS . See odeoptions.

Программы решения

Тип задачи, которую надо решить и используемый метод зависят от значения первого необязательного аргумента type , который может быть одной из следующих строк:

Программа решения lsoda из пакета ODEPACK вызывается по умолчанию. Она автоматически выбирает между нежёстким методом прогноза-исправления Адамса (predictor-corrector Adams method) и жёстким методом обратной дифференциальной формулой (ОДФ) ( Backward Differentiation Formula (BDF) method). Изначально она применяет нежёсткий метод и динамически проверяет данные для того, чтобы решить какой метод использовать.

Используется для нежёстких задач. Вызывается программа решения lsode из пакета ODEPACK, и она использует метод Адамса.

Это для жёстких задач. Вызывается программа решения lsode из пакета ODEPACK, и она использует метод ОДФ.

Адаптивный метод Рунге-Кутты 4-го порядка (RK4).

Используется программа Шампайна и Уотса (Shampine и Watts), основанная на методе Рунге-Кутты-Фелберга пары 4 и 5-го порядка (RKF45). Она для нежёстких и среднежёстких задач, когда получаемые вычисления не дороги. Этот метод не следует, в общем случае, использовать, если пользователь требует высокую точность.

Та же программа решения, что и «rkf» , но пользовательский интерфейс очень прост, т. е. программе решения могут быть переданы только параметры rtol и atol . Это самый простой метод для пробы.

Программа решения ОДУ с возможностью нахождения корней. Используется программа решения lsodar из пакета ODEPACK. Она является вариантом программы решения lsoda , где она ищет корни заданной векторной функции. См. справку по ode_root.

Моделирование дискретного времени. См. справку по ode_discrete.

Примеры

В следующем примере мы решим обыкновенное дифференциальное уравнение dy/dt=y^2-y*sin(t)+cos(t) с начальным условием y(0)=0 . Используем программу решения по умолчанию.

В следующем примере мы решаем уравнение dy/dt=A*y . Точное решение равно y(t)=expm(A*t)*y(0) , где expm — матричная экспонента. Неизвестное равно матрице y(t) размером 2 на 1.

В следующем примере мы решаем ОДУ dx/dt = A*x(t) + B*u(t) с u(t)=sin(omega*t) . Обратите внимание, что дополнительные аргументы f : A , u , B , omega передаются в f в списке.

В следующем примере мы решим дифференциальное уравнение Риккати dX/dt=A’*X + X*A — X’*B*X + C , где начальное условие X(0) является единичной матрицей 2 на 2.

В следующем примере мы решаме дифференциальное уравнение dY/dt=A*Y , где неизвестная Y(t) является матрицей 2 на 2. Точное решение равно expm Y(t)=expm(A*t) , где expm — матричная экспонента.

С компилятором

Следующий пример требует компилятор C.

Смотрите также

• ode_discrete — программа решения обыкновенных дифференциальных уравнений, моделирование дискретного времени
• ode_root — программа решения обыкновенных дифференциальных уравнений с поиском корней
• dassl — дифференциальное алгебраическое уравнение
• impl — дифференциальное алгебраическое уравнение
• odedc — программа решения дискретно-непрерывных ОДУ
• odeoptions — установка опций для программ решения ОДУ
• csim — simulation (time response) of linear system
• ltitr — discrete time response (state space)
• rtitr — discrete time response (transfer matrix)
• intg — определённый интеграл

Литература

Alan C. Hindmarsh, «lsode and lsodi, two new initial value ordinary differential equation solvers», ACM-Signum newsletter, vol. 15, no. 4 (1980), pp. 10-11.

Дифференциальные уравнения по-шагам

Результат

Примеры дифференциальных уравнений

• Простейшие дифференциальные ур-ния 1-порядка
• Дифференциальные ур-ния с разделяющимися переменными
• Линейные неоднородные дифференциальные ур-ния 1-го порядка
• Линейные однородные дифференциальные ур-ния 2-го порядка
• Уравнения в полных дифференциалах
• Решение дифференциального уравнения заменой
• Смена y(x) на x в уравнении
• Другие

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте: