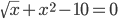Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Программа для метода бисекции
Дана функция f (x) с плавающим числом x и двумя числами «a» и «b» такая, что f (a) * f (b) 3 + a 2 x 2 +… .. + e, где aa 1 , a 2 ,… — константы, а x — переменная ,
Трансцендентальной функцией являются неалгебраические функции, например, f (x) = sin (x) * x — 3 или f (x) = e x + x 2 или f (x) = ln (x) + x….
Что такое метод деления пополам?
Этот метод также называется методом деления пополам, методом двоичного поиска или методом дихотомии. Этот метод используется, чтобы найти корень уравнения в заданном интервале, который является значением «x», для которого f (x) = 0.
Метод основан на теореме о промежуточном значении, которая гласит, что если f (x) — непрерывная функция и существуют два действительных числа a и b, такие что f (a) * f (b) 0 и f (b)
Ниже приведена реализация вышеуказанных шагов.
// C ++ программа для реализации метода Bisection для
// решение уравнений
#include
using namespace std;
#define EPSILON 0.01
// Пример функции, решение которой определяется с помощью
// Метод деления пополам. Функция х ^ 3 — х ^ 2 + 2
double func( double x)
return x*x*x — x*x + 2;
// Печатает корень функции func (x) с ошибкой EPSILON
void bisection( double a, double b)
if (func(a) * func(b) >= 0)
cout «You have not assumed right a and b\n» ;
while ((b-a) >= EPSILON)
// Найти среднюю точку
// Проверяем, является ли средняя точка корневой
// Определим сторону, чтобы повторить шаги
else if (func(c)*func(a)
cout «The value of root is : «
// Программа драйвера для проверки вышеуказанной функции
// Предполагаемые начальные значения
double a =-200, b = 300;
// Java-программа для реализации метода Bisection
// для решения уравнений
static final float EPSILON = ( float ) 0.01 ;
// Пример функции, решение которой определяется с помощью
// Метод деления пополам. Функция х ^ 3 — х ^ 2 + 2
static double func( double x)
return x*x*x — x*x + 2 ;
// Печатает корень функции func (x) с ошибкой EPSILON
static void bisection( double a, double b)
if (func(a) * func(b) >= 0 )
System.out.println( «You have not assumed»
while ((b-a) >= EPSILON)
// Найти среднюю точку
// Проверяем, является ли средняя точка корневой
// Определим сторону, чтобы повторить шаги
else if (func(c)*func(a) 0 )
// выводит значение c до 4 десятичных знаков
System.out.printf( «The value of root is : %.4f»
// Программа драйвера для проверки вышеуказанной функции
public static void main(String[] args)
// Предполагаемые начальные значения
double a =- 200 , b = 300 ;
// Этот код предоставлен Нирмал Патель
# Python программа для реализации
Метод деления пополам
# решение уравнений
# Пример функции, чья
# решение определяется с помощью
Метод деления пополам.
# Функция x ^ 3 — x ^ 2 + 2
return x * x * x — x * x + 2
# Печатает корень функции (x)
# с ошибкой EPSILON
if (func(a) * func(b) > = 0 ):
print ( «You have not assumed right a and b\n» )
while ((b — a) > = 0.01 ):
# Найти среднюю точку
# Проверьте, является ли средняя точка корневой
# Решите сторону повторить шаги
if (func(c) * func(a) 0 ):
print ( «The value of root is : » , «%.4f» % c)
# Код драйвера
# Предполагаемые начальные значения
# Этот код добавлен
# Анант Агарвал.
// C # программа для реализации
// Метод деления пополам
// решение уравнений
static float EPSILON = ( float )0.01;
// Пример функции, чья
// решение определяется с помощью
// Метод деления пополам. Функция
// это х ^ 3 — х ^ 2 + 2
static double func( double x)
// Печатает корень функции func (x)
// с ошибкой EPSILON
static void bisection( double a,
if (func(a) * func(b) >= 0)
Console.WriteLine( «You have not assumed» +
while ((b — a) >= EPSILON)
// Найти среднюю точку
// точка является корнем
else if (func(c) * func(a)
// выводит значение c
// до 4 десятичных знаков
Console.WriteLine( «The value of » +
static public void Main ()
// Предполагаемые начальные значения
double a = -200, b = 300;
// Этот код предоставлен ajit
// PHP программа для реализации
// Метод деления пополам
// уравнения
// Пример функции, чья
// решение определено
// используя метод деления пополам.
// Функция x ^ 3 — x ^ 2 + 2
function func( $x )
// Печатает корень функции func (x)
// с ошибкой EPSILON
function bisection( $a , $b )
echo «You have not assumed » .
«right a and b» , «\n» ;
while (( $b — $a ) >= $EPSILON )
// Найти среднюю точку
// точка является корнем
else if (func( $c ) * func( $a )
echo «The value of root is : » , $c ;
// Предполагаемые начальные значения
// Этот код предоставлен ajit
?>
Выход:
Временная сложность: — Временная сложность этого метода зависит от предполагаемых значений и функции.
Какие плюсы и минусы?
Преимущество метода деления пополам состоит в том, что он гарантированно сходится. Недостатком метода деления пополам является то, что он не может обнаружить несколько корней.
В целом, метод деления пополам используется для получения начального грубого приближения решения. Затем более быстрые методы сходятся, чтобы найти решение.
Вскоре мы обсудим другие методы решения алгебраических и трансцендентных уравнений.
Эта статья предоставлена Абхираджем Смитом . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме
Метод бисекции
Метод бисекции или метод деления отрезка пополам — простейший численный метод приближённого нахождения корня уравнения.
Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.
Метод бисекции
Метод бисекции
Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)». На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).
Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т. е. сходимость метода всегда равна сходимости в наихудшем случае.
Итерационная формула проста:
Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.
http://espressocode.top/program-for-bisection-method/
http://planetcalc.ru/3718/