Решение уравнений с одной переменной
Лабораторная работа № 1
Решение уравнений средствами программы Microsoft Excel: «подбор параметра» и «поиск решения»
Цель работы: приобрести навыки решения уравнений средствами программы Microsoft Excel: «Подбор параметра» и «Поиск решения»
Сведения из теории
Программа Microsoft Excel относится к классу программ, называемых электронными таблицами. Электронные таблицы ориентированы, прежде всего, на решение экономических и инженерных задач, позволяют систематизировать данные из любой сферы деятельности.
Программа Microsoft Excel позволяет:
а) сформировать данные в виде таблиц;
б) рассчитать содержимое ячеек по формулам, при этом возможно использование более 300 встроенных функций;
в) представить данные из таблиц в графическом виде;
г) организовать данные в конструкции, близкие по возможностям, к базе данных.
Решение уравнений с одной переменной
Задачи, в которых используются уравнения с одной переменной можно решать методом перебора, однако в лучшем случае на это уходит много времени.
Можно предложить другие способы решения. В Excel они реализованы как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.
 |
Эту процедуру используют для поиска такого значения ячейки, при котором значение другой ячейки, вычисляемое по формуле, заранее задано. В формуле должна быть ссылка на ячейку, значения которой ищут. Ограничения на искомое значение ячейки не налагают.
Познакомимся с этой процедурой на примере составления штатного расписания.
Пусть известно, что в штате отдела ДПС состоит 15 постовых, 3 старших наряда, 1 ком. взвода, начальник отделения, зам. нач. отделения, бухгалтер, зам.нач ДПС, начальник ДПС. Общий месячный фонд зарплаты составляет 70000 руб.. Необходимо определить, какими должны быть оклады сотрудников отдела.
Построим модель решения этой задачи. За основу возьмем оклад постового, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*C+Bb где С — оклад постового; А, и В; — коэффициенты, которые для каждой должности определяют следующим образом:
• Старший наряда получает в 1,5 раза больше постовой (А2=1,5: В2=0);
• Ком. взвода — в 3 раза больше постового (В3=0; А3=3);
• Нач. отделения — на 300 руб. больше, чем ком. взвода (А4=3; В4=300);
• Зам. нач. отделения — в 2 раза больше постового (A5=2; B5=0);
• бухгалтер — на 400 руб. больше старшего наряда (А6,= 1,5: В6,=400);
• зам. нач. ДПС — в 4 раза больше постового (А7-4; В7=0);
• начальник ДПС — на 200 руб. больше зам. нач. ДПС (A8=4; B8=200);
Зная количество человек на каждой должности, нашу модель можно записать как уравнение:
где N1 — число постовых. N2 – старших наряда и т.д.
В этом уравнении нам известны A1..A8, В1. В8 и N1. N8. а С неизвестно.
Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С. Решим его.
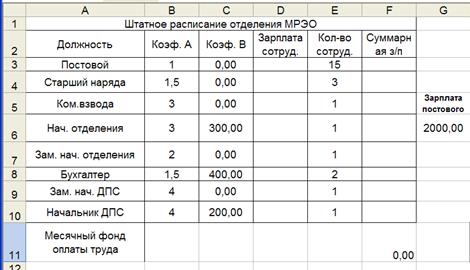
Введём исходные данные в рабочий лист электронной таблицы, как показано на рисунке 1.
В столбце D вычислим заработную плату для каждой должности. Например, дляячейки D3 формула расчета имеет вид =В3*$G$6+С3.
В столбце F вычислим заработную плату всех рабочих данной должности. Например, для ячейки F3 формула расчета имеет вид =D3*E3.
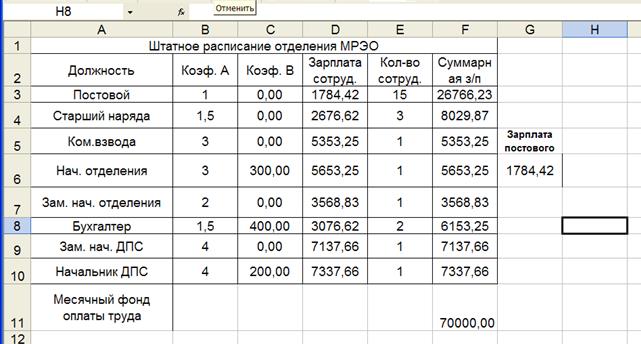
В ячейке F11 вычислите суммарный фонд заработной платы отдела ДП
С. Рабочий лист электронной таблицы будет выглядеть, как показано на рисунке 2.
Определим оклад постового так, чтобы расчетный фонд был равен заданному:
а) активизируем команду Подбор параметра из меню Сервис,
б) в поле «Установить в ячейке» появившегося окна введём ссылку на ячейку F11. содержащую формулу;
в) в поле «Значение» наберём искомый результат 70000;
г) в поле «изменяя значение ячейки» введём ссылку на изменяемую ячейку G6 и щелкните на кнопке ОК.
Сохраним таблицу. Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, — это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.
Задачи оптимизации
В предыдущем подразделе, мы рассмотрели задачу поиска значения параметра, позволяющего достичь конкретной цели.
Решаемые задачи могут быть более сложными. Например, поиск нескольких параметров, обеспечивающих некоторый наперед заданный результат.
Кроме того, иногда интересует не конкретный результат, а минимально или максимально возможный. Например, как минимизировать затраты на содержание персонала.
Такие задачи в Excel решают с помощью Поиска решения.























 ВВЕДЕНИЕ
ВВЕДЕНИЕ
В данный момент существует много программ для решения уравнений, вычисления интегралов и дифференциалов: MathCAD, MATLAB, и т.д. Они имеют высокую точность вычисления, высокую функциональность, но имеют и свои недостатки. Главные из них – сложный непонятный интерфейс, высокая многофункциональность недоступна рядовому пользователю.
Рынок нуждается в более простых аналогах приведенных выше программ. Созданный программный продукт способен решать уравнения с одной переменной методом Ньютона (касательных). Он прост в эксплуатации, имеет интуитивно понятный интерфейс и способен выстраивать график уравнения, что является очень важным для пользователя.
Программа будет полезна всем, как студентам высших учебных заведений, так и школьникам.
1. ПОСТАНОВКА ЗАДАЧИ
Цель создания программного продукта
Главной целью работы является разработка программы способной решать уравнения с одной переменной методом Ньютона (касательных), что должно являться пособием для студентов высших учебных заведений и для учащихся математических классов среднеобразовательных школ в снижении ненужной нагрузки, связанной с многочисленными массивами вычислений.
1.2. Постановка задачи
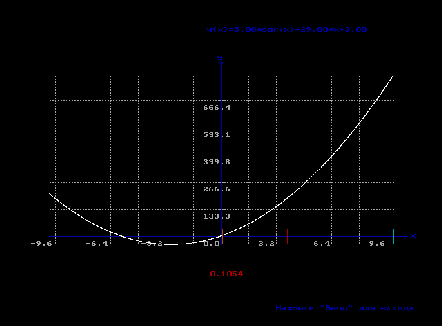
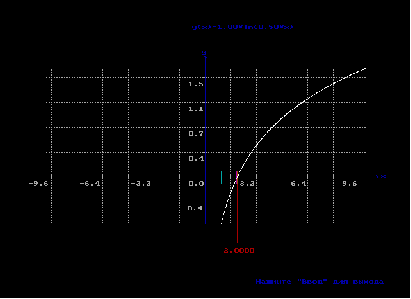
В данном программном продукте необходимо реализовать решение двух видов уравнений: y(x) =a×ln(b×x), y(x) =ax2+bx+c. Вместо коэффициентов должны использоваться параметры a, b, c, которые принимают значения, вводимые пользователем. Для нахождения корней, обязательным является указание промежутков, на которых определена функция, поэтому пользователь обязательно вводит промежутки функции m, n. Метод Ньютона является итерационным методом, следовательно, должна указываться погрешность вычисления ε. Обязательным является построение графика выбранной функции на заданном промежутке.
2. МАТЕМЕТИЧЕСКАЯ МОДЕЛЬ
Дисциплина «Численные методы» содержит набор методов и алгоритмов приближенного (численного) решения разнообразных математических задач, для которых точное аналитическое решение либо не существует, либо слишком сложно для использования на практике. При численном решении задач всегда возникает погрешность.
Выделяют абсолютную и относительную погрешность. Пусть р – точное значение искомого ответа, а p – приближённое значение, полученное с помощью численного метода.
Тогда – абсолютная погрешность,
На первом этапе необходимо найти отрезок [a,b], на котором функция имеет ровно один корень. На втором этапе происходит уточнение корня на отрезке с заданной точностью с помощью одного из численных методов.
Метод, реализуемый в РУОП, называется методом Ньютона. Другое название метода – метод касательных.
где f(x) C» [m,n], f(m) f(n) x
Графическая иллюстрация метода приведена на рисунке 2.1. Начальная точка в этом случае совпадает с n.
Рисунок 2.1. – Метод Ньютона
Идея метода заключается в том, что последовательность приближений к корню строится путем проведения касательных к графику функции и нахождения их точек пересечения с осью ОХ.
Шаг 1. Найти первое приближение к корню x0 по формуле (2.2).
Шаг 2. Находить следующие приближения к корню по формуле (2.1), пока не выполнится условия окончания:
Рисунок 3.2. – Корень уравнения
Точка ξ, для которой выполняется ξ= φ(ξ), называется неподвижной точкой процесса итераций. Очевидно, что эта точка является корнем уравнения f(x) =0.
Константа С подбирается таким образом, чтобы функция φ(x) удовлетворяла условиям сходимости метода итераций:
1) – является непрерывной и дифференцируемой на [m,n] ;
Если , то С нужно выбирать так, чтобы и для .
Метод состоит в построении последовательности приближений к корню. В качестве начального приближения выбирается любая точка x0 [a,b]. Для определенности можно брать середину отрезка [a,b]. В качестве формулы получения последующих приближений выступает сама φ(x):
Шаг 1. Найти первое приближение к корню x0 как середину отрезка [m,n].
Шаг 2. Находить следующие приближения к корню по формуле, пока не выполнится условия окончания:
|xi — xi+1| Подсказки при вводе данных
Сообщение об ошибке ввода
вывода результатов на экран
Варианты сохранения результатов
Значение корня уравнения
Рисунок 5.1 – Схема информационных потоков
Блок построения графика
Блок помощи и справочной информации
Файл справочной информации
Помощь и справочная информация
Блок выхода из программы
Рисунок 5.1 – Схема информационных потоков (продолжение)
– Данные, ввидение которых возможно
как из файлов, расположенных на
жёстком диске, так и с клавиатуры;
–Данные, выводимые на экран;
Данные, вводимые из файла.
5.2. Описание функционирования программы
При запуске программы на экране появляется титульный лист, отображающий информацию о студенте; далее загружается меню программы, состоящее из пяти пунктов:
y ( x )= a * ln ( b * x )
Рисунок 5.2 – Схема функционирования программы
– y ( x ) = a * ln ( b * x )
Пункт «Справка» включает в себя информацию о методе Ньютона. Пункты «y(x) =a*ln(b*x)» и «y(x) =a*x^2+b*x+c» представляют собой решения уравнений, где задаются промежутки m и n, параметры a, b(, c), погрешность E и выполняется сохранение в файлы. Пункт «Построение графика» строит график выбранного уравнения в зависимости от введённых параметров и промежутков. Пункт «Выход» – выход из программы. Схема функционирования представлена на рисунке 5.2.
5.3. Описание процедур и функций программы
Procedure title () – выводит титульную страницу на экран монитора;
Procedure graphica () – инициализирует графику.
Procedure pro () – содержит в себе переменную р, которая отвечает за номер выделяемой кнопки, передаётся как параметр в procedure key (p) и в procedure eat (p, bool), а также содержит в себе переменную bool, отвечающую за цикл в рамках procedure pro, передаётся как параметр в procedure eat (p2, bool);
Procedure eat (p2: byte; var bool: boolean) – в зависимости от параметра p2 выполняет один из пяти вариантов дальнейших действий программы. Переменная bool передаётся как параметр обратно в procedure pro;
Procedure key (p1: byte) – выстраивает графическую картинку меню в зависимости от параметра р1;
Procedure equation_1 () – решение уравнения вида y(x) =a×ln(b×x). Переменная Е (погрешность) принимается как параметр из procedure load_file_3 (E), передаёт переменную Е как параметр в procedure save_file (E);
Procedure equation_2 () – решение уравнения вида y(x) =a×x2+b×x+c. Переменная Е (погрешность) принимается как параметр из procedure load_file_3 (E), переменная Е передаётся как параметр в procedure save_file (E);
Procedure load_file_1 () – загружает переменные m и n (промежутки функции) из файла, либо обеспечивает их ввод с клавиатуры, в зависимости от желания пользователя. m, n – глобальные переменные в рамках программы;
Procedure load_file_2 () – загружает переменные a и b либо a, b, c (в зависимости от вида функции) (коэффициенты уравнения) из файла, либо обеспечивает их ввод с клавиатуры, в зависимости от желания пользователя. a, b, c – глобальные переменные в рамках программы;
Procedure load_file_3 (var E: real) – загружает переменную Е (погрешность функции) из файла, либо обеспечивает их ввод с клавиатуры, в зависимости от желания пользователя. Е передаётся как параметр и принимается как переменная в procedure equation_1 и equation_2;
Procedure save_file (E: real) – сохраняет переменные a, b, (c,) m, n – глобальные в рамках программы в файлы либо не сохраняет, сохраняет переменную Е в виде параметра в файл, либо не сохраняет;
Procedure groffunc () – выстраивает график по значениям глобальных в рамках программы переменных a, b, (c,) m, n, с отмеченными на оси х приближениями и корнем уравнения. Содержит в себе function f (x: real): real, высчитывающую значение одной из функций в зависимости от аргумента х. Переменные у0 (масштаб) и у2 (максимальное значение функции) передаются в виде параметров в procedure setka (y0, y2);
Procedure setka (yn: integer; y2: real) – выстраивает координатную сетку и оцифровку осей x и y в зависимости от глобальных в рамках программы переменных m, n и параметров yn и y2;
Procedure help () – предоставляет пользователю непосредственную методологическую помощь.
5.4. Схема взаимодействия процедур программы
Для наглядности работы подпрограмм программы необходимо изобразить в виде схемы их взаимодействие между собой. Взаимодействие подпрограмм изображено на рисунке 5.3.
procedure eat (p2 : integer; var bool : boolean);
Procedure save_file (E : real);
load_file_3 (var E : real);
procedure setka (yn: integer; y2 : real);
Рисунок 5.3 – Взаимодействие процедур программы
– запуск процедуры на которую указывает стрелка, из процедуры из которой она исходит.
5.5. Перечень обозначений
5.5.1 Обозначения вводимых данных
m, n – промежутки функции;
a, b, c – коэффициенты уравнения, представленные в виде параметров;
E – погрешность, аналог ε в разделе «Описании математической модели» и в разделе «Описание (и обоснование выбора) метода решения».
5.5.2 Обозначения выводимых данных
y(x) =a*ln(b*x), y(x) =a*x^2+b*x+c – уравнения используемые в программе;
x – неизвестная, корень уравнения;
x^2 – неизвестная x в степени 2.
5.6 Входные и выходные данные
5.6.1 Входные данные
y(x) =a*ln(b*x), y(x) =a*x^2+b*x+c – функция;
m, n: real – левый и правый промежутки функции соответственно;
a, b, c: real – параметры, коэффициенты уравнения;
E: real – погрешность;
«Помощь и справочная информация».
5.6.2 Выходные данные
x1: real – значение корня уравнения;
st: string – текстовые сообщения, возникающие в процессе выполнения программы (ошибки и варианты дальнейшего продолжения).
5.6.3 Промежуточные данные
Bool_of: Boolean – определяет цикл выполнения алгоритма решения;
mass: real – массив [1. . 20] ;
number: byte – глобальная переменная, номер функции;
code_of: byte – переменная, отвечающая за необходимость поиска корня уравнения;
root: real – разность приближений.
5.7. Алгоритм решения задачи
5.7.1. Алгоритм нахождения корня уравнения y(x) =a×ln(b×x)
Алгоритм решения уравнения вида y(x) =a×ln(b×x) приводится на рисунке 5.4.
пока (( m n ) и ((( m n m > 0) и ( n > 0))));
Методика изучения темы «Уравнения с одной переменной»
методическая разработка по алгебре (7 класс) на тему
В статье изложены методические рекомендации при изучении темы «Уравнения с одной переменной». Разработан комплекс упражнений, предназначенных для обучения решения линейных уравнений и решения текстовых задач с использованием аппарата уравнений. Рассмотрены различные методы их решения.
Скачать:
| Вложение | Размер |
|---|---|
| Методика изучения темы «Уравнения с одной переменной» | 51.14 КБ |
Предварительный просмотр:
Методика изучения темы «Уравнения с одной переменной»
1. Анализ содержания программы по математике
Изучение темы «Уравнения с одной переменной» курса алгебры 7 класса входит в программу экзамена. Поэтому контроль знаний, умений и навыков учащихся очень важен при изучении данного раздела алгебры, от этого зависит успешность сдачи экзамена. Для того чтобы определиться с выбором форм проверки, необходимо выделить содержание контроля. Для начала необходимо сделать анализ программы, затем анализ содержания темы учебника, а затем, в соответствии с ним, выбрать формы и методы контроля.
В курсе алгебры в 7 классе содержатся задания теоретического и прикладного характера. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Целью изучения этого курса является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и другие), усвоение аппарата функций как основного средства математического моделирования, решение прикладных задач, осуществление функциональной подготовки школьников.
В связи с этим программа курса математики предполагает следующее содержание по изучению линейных уравнений с одной переменной в 7 классе основной школы:
– Уравнение с одной переменной. Корни уравнения. Линейное уравнение.
– Решение текстовых задач методом составления уравнений.
В соответствии с программой требования к математической подготовке учащихся:
– понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики;
– правильно употреблять термины «уравнение», «корень уравнения», понимать их в тексте, в речи учителя, понимать формулировку задачи «решить уравнение»;
– решать линейные уравнения;
– решать текстовые задачи с использованием уравнений.
При организации учебного процесса следует опираться на тематическое планирование учебного материала, в котором разработано поурочное планирование, ориентированное на учебник алгебры 7 класса.
Анализ содержания тем, связанных с изучением уравнений позволяет продумать эффективный систематический контроль.
2. Уравнения с одной переменной
1). Уравнение и его корни
Уравнением с одной переменной, называется равенство, содержащее только одну переменную.
Корнем уравнения называется значение переменной, при котором уравнение превращается в верное числовое равенство.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
2). Линейное уравнение с одной переменной
Уравнение вида ax = b , где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Уравнения, имеющие одни и те же корни, называются равносильными уравнениями.
Уравнения, не имеющие корней, также считают равносильными.
Свойство 1. При переносе слагаемого из одной части уравнения в другую с противоположным знаком, получается уравнение, равносильное данному.
Свойство 2 . При умножении или делении обеих частей уравнения на одно и то же число, отличное от нуля, мы получим уравнение, равносильное данному.
Принято: цифры в алгебраических выражениях заменять
первыми буквами латинского алфавита – a , b , c , …,
а переменные обозначать последними – x , y , z .
Сколько корней может иметь уравнение ?
Если a ≠ 0, b – любое значение, уравнение ax = b имеет один корень x = b : a ;
a = 0, b ≠ 0 – ax = b не имеет корней;
a = 0, b = 0 – ax = b имеет бесконечно много корней.
3 x = 3, один корень x = 3 : 3 x = 1;
0 · x = 5 корней нет;
0 · x = 0 бесконечно много корней: x – любое число.
3. Примеры уранений и алгоритмы решения уравнений.
Пример 1 . Решите уравнение: 4 х = 32.
Корнем уравнения является х = 8, так как 4·8 = 32 верное равенство.
Пример 2 . Решите уравнение .
Уравнение имеет два корня:
х + 5 = 2 или 2) х + 5 = – 2
Пример 3 . Решите уравнение – 2( х + 6) = x + 6 .
Шаг 1. Раскроем скобки: – 2 х – 12 = х + 6.
Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую. При переносе через знак равенства, знак, стоящий перед соответствующим членом уравнения, меняется на противоположный:
Шаг 3. Приведем подобные члены: – 3 х = 18.
Шаг 4. Находим х : х = – 6.
Пример 4. Решите уравнение 2 t – 3(2 – 6 t ) = 4( t + 6).
Шаг 1. Раскроем скобки: 2 t – 6 +18 t = 4 t +24.
Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую: 2 t – 4 t +18 t = 24 + 6.
Шаг 3. Приведем подобные члены: 16 t = 30.
Шаг 4. Находим неизвестное и записываем ответ:
Пример 5. Решите уравнение (7 х – 2)(3 – 5 х ) =0.
Условие равенства нулю произведения: произведение двух выражений равно нулю тогда и только тогда, когда одно из этих выражений обращается в нуль, а другое при этом не теряет смысла.
В данном примере оба сомножителя определены для любого действительного числа х, т.е. при любом значении числа х ни один из сомножителей не теряет смысла, следовательно, равенство нулю произведения равносильно совокупности условий: либо один, либо другой сомножитель равен нулю. При увеличении числа сомножителей, соответственно увеличивается количество условий.
7 х – 2 = 0 или 3 – 5 х =0;
Пример 6 . Решите уравнение 0,5 (1 – 8 х ) – 1,5(6 х – 3) = 3 х –13.
Шаг 1. Раскроем скобки: 0,5 – 4 х – 9 х + 4,5 = 3 х – 13.
Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую: – 8 х – 9 х – 3 х = – 13 – 4,5 – 0,5.
Шаг 3. Приведем подобные члены: – 18 х = – 18.
Шаг 4. Находим неизвестное и записываем ответ: х = 1.
Пример 7. Решите уравнение – – = 1.
Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 28:
7(3 х + 5) – 4(6 х –2) = 28;
21 х + 35 – 24 х + 8 = 28;
4. Решение задач с помощью уравнений
При решении задач с помощью уравнений необходимо следовать определенному алгоритму:
1) Обозначить некоторое неизвестное число буквой;
2) используя условие задачи, составить уравнение;
3) решить уравнение;
4) полученный результат привести в соответствие с условием задачи.
Пример 8. Периметр прямоугольника 28 см, причем одна из его сторон на 4 см больше, чем другая. Найти стороны и площадь прямоугольника.
1) Пусть ширина прямоугольника х см, тогда его длина ( х + 4) см.
2) Из условия задачи известно, что периметр прямоугольника равен 28 см, составим уравнение: .
3) Решим уравнение: .
Значит, ширина прямоугольника равна 5 см.
4) Зная ширину прямоугольника и зависимость длины от ширины, найдем сначала его вторую сторону, а затем и площадь.
х + 4 = 5 + 4 = 9 (см), (см 2 ).
Ответ: 9 см, 45 см 2 .
Пример 9. Один арбуз на 5 кг легче, чем второй и в 3 раза легче, чем третий. Первый и третий вместе в 2 раза тяжелее, чем второй. Найти массу второго арбуза.
Пусть первый арбуз весит х кг, тогда второй – ( х + 5) кг, а третий – 3 х кг.
2) По условию первый и третий в 2 раза тяжелее второго, составим и решим уравнение:
Значит, 5 кг весит первый арбуз, 5 + 5 = 10 (кг) – второй, а 3×5 =15(кг) – третий арбуз.
Ответ: 5кг; 10 кг; 15 кг.
Пример 10. Катер преодолевает расстояние между пунктами А и В, двигаясь по течению, за 2 часа. На обратный путь он затрачивает 3 часа, двигаясь с той же скоростью. Какое расстояние преодолевает катер на маршруте, и какова его собственная скорость, если скорость течения 5 км/ч ?
1) Пусть х км/ч – собственная скорость катера. Тогда ( х + 5) км/ч – скорость катера по течению, а ( х – 5) км/ч – скорость катера против течения.
2) Учитывая время движения катера, составим уравнение: .
3) Решим уравнение:
2 х + 10 = 3 х – 15;
Значит, 25 км/ч – собственная скорость катера.
4) (25 + 5)·2 = 60 (км) – расстояние, которое преодолевает катер на маршруте.
Ответ: 60 км, 25 км/ч.
Из пунктов А и В навстречу друг другу выехали одновременно два велосипедиста, мужчина и женщина. Скорость мужчины была на 3 км/ч больше. Через два часа они встретились, а еще через 3 часа женщина прибыла в пункт А.
Какое расстояние (S) между этими пунктами?
1) Пусть х км/ч – скорость женщины,
Тогда ( х +3) км/ч – скорость мужчины.
Скорость сближения (их совместная скорость) – (2 х + 3) км/ч,
2) Весь путь мужчина и женщина преодолели за 2 часа, а женщина на весь путь затратила 5 часов, учитывая это, составим уравнение:
3) Решим уравнение:
Значит, 6 км/ч – скорость женщины.
4) 6 + 3 = 9 (км/ч) – скорость мужчины.
Тогда расстояние между пунктами А и В:
Пример 12. Отцу 42 года, а сыну 15 лет. Через сколько лет сын будет в два раза моложе отца?
Решение.
1) Пусть х – количество лет, через которое сын будет в два раза моложе отца.
2) Тогда можно составить уравнение:
3) Решим уравнение:
Ответ: через 12 лет.
В некоторых случаях при решении задачи целесообразно составить таблицу.
Пример 13. В корзине яблок в 4 раза меньше, чем в ящике. После того как из ящика переложили в корзину 1,5 кг яблок, в корзине стало в 3 раза меньше яблок, чем в ящике. Сколько килограммов яблок было в корзине и ящике сначала?
http://doc4web.ru/informatika/razrabotka-programmnogo-obespecheniya-dlya-resheniya-uravneniy-s.html
http://nsportal.ru/shkola/algebra/library/2014/10/17/metodika-izucheniya-temy-uravneniya-s-odnoy-peremennoy



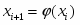
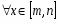
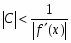
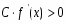
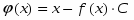
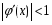
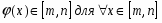
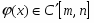
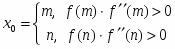
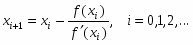
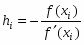
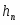
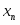
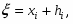
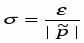
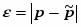 ВВЕДЕНИЕ
ВВЕДЕНИЕ