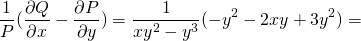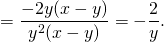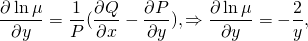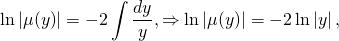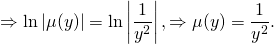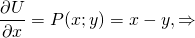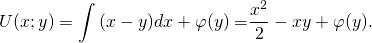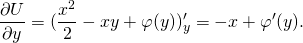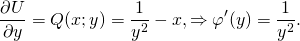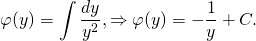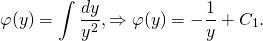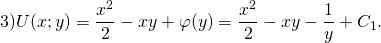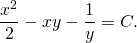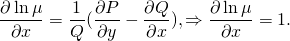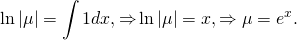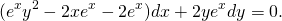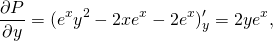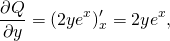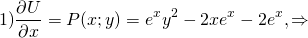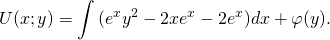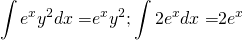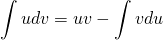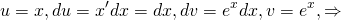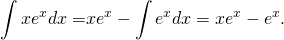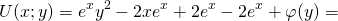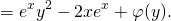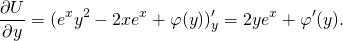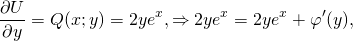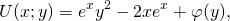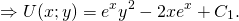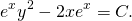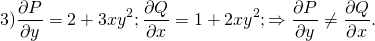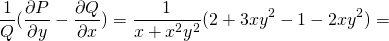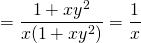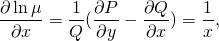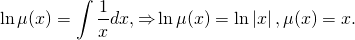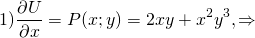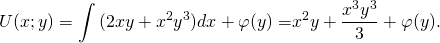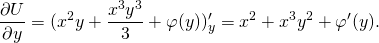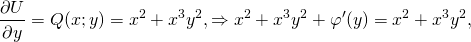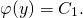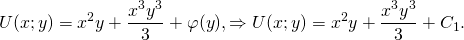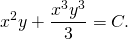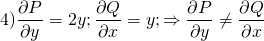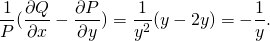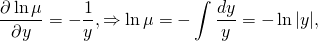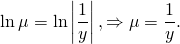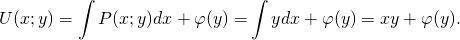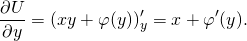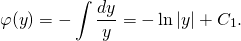Примеры на интегрирующий множитель
Проиллюстрируем применение интегрирующего множителя в решении дифференциальных уравнений. Рассмотрим примеры на интегрирующий множитель.
1) Проинтегрировать уравнение (xy²-y³)dx+(1-xy²)dy=0.
1. ∂P/∂y=∂(xy²-y³)/∂y=2xy-3y²; ∂Q/∂x=∂(1-xy²)/∂x=-y². Поскольку ∂P/∂y≠∂Q/∂x, это уравнение не является уравнением в полных дифференциалах. Здесь
Таким образом, интегрирующий множитель не зависит от x и ищем его как функцию от y: µ=µ(y). В этом случае
интегрируя полученное равенство, имеем:
2. Теперь умножим обе части исходного уравнения (xy²-y³)dx+(1-xy²)dy=0 на найденный интегрирующий множитель µ(y)=1/y². Получаем:
(x-y)dx+(1/y²-x)dy=0. Проверяем, действительно ли получили уравнение в полных дифференциалах: ∂P/∂y=∂(x-y)/∂y=-1, ∂Q/∂x=∂(1/y²-x)/∂x=-1. То есть ∂P/∂y=∂Q/∂x, необходимое и достаточное условие выполнено, а значит, это уравнение в полных дифференциалах .
2) Дифференцируем полученную функцию U(x;y) по y:
Проинтегрировав получившееся равенство, находим
А поскольку интеграл уравнения в полных дифференциалах dU(x;y)=0 есть U(x;y)=C, то получаем, что
2) Решить уравнение (y²-2x-2)dx+2ydy=0.
1. ∂P/∂y=∂(y²-2x-2)/∂y=2y, ∂Q/∂x=∂(2y)/∂x=0. Поскольку ∂P/∂y≠∂Q/∂x, это уравнение не является уравнением в полных дифференциалах.Но (1/Q)(∂P/∂y-∂Q/∂x)=(1/2y)(2y-0)=1. Таким образом, интегрирующий множитель не зависит от y и ищем его как функцию от x: µ=µ(x). В этом случае
Интегрируем полученное равенство:
2. Умножаем обе части исходного уравнения (y²-2x-2)dx+2ydy=0 на интегрирующий множитель:
Проверяем выполнение необходимого и достаточного условия:
∂P/∂y=∂Q/∂x, а значит, полученное уравнение является уравнением в полных дифференциалах.
А второй интеграл ищем по формуле интегрирования по частям:
2) Теперь дифференцируем полученную функцию U(x;y) по y:
А поскольку интеграл уравнения в полных дифференциалах dU(x;y)=0 есть U(x;y)=C, то получаем, что
Задания для самопроверки:
Решить уравнения, допускающие интегрирующий множитель вида µ=µ(x) или µ=µ(y):
3) (2y+xy³)dx+(x+x²y²)dy=0;
4) y²dx+(xy-1)dy=0.
Таким образом, необходимое и достаточное условие не выполнено, в левой части нет полного дифференциала. Найдем
Так как получили выражение не зависящее от y, то ищем µ=µ(x). Тогда
2. Умножаем обе части исходного уравнения на интегрирующий множитель: (2xy+x²y³)dx+(x²+x³ y²)dy=0. проверяем: ∂P/∂y=∂(2xy+x²y³)/∂y=2x+3x²y²; ∂Q/∂x=∂(x²+x³ y²)/∂x=2x+3x²y². Таким образом, условие ∂P/∂y=∂Q/∂x выполнено, а значит, получили уравнение в полных дифференциалах.
2) Теперь дифференцируем полученную функцию U(x;y) по y:
А поскольку интеграл уравнения в полных дифференциалах dU(x;y)=0 есть U(x;y)=C, то получаем, что
Значит, данное уравнение не является уравнением в полных дифференциалах. Но
Таким образом, интегрирующий множитель не зависит от x и ищем его как функцию от y: µ=µ(y). В этом случае
2. Теперь умножим обе части исходного уравнения y²dx+(xy-1)dy=0 на интегрирующий множитель 1/y: ydx+(x-1/y)dy=0. Проверяем выполнение необходимого и достаточного условия: ∂P/∂y=∂(y)/∂y=1, ∂Q/∂x=∂(x-1/y)/∂x=1, то есть ∂P/∂y=∂Q/∂x. Таким образом, получено уравнение в полных дифференциалах.
1) ∂U/∂x=P(x;y)=y, отсюда
2) Теперь дифференцируем U(x;y) по y:
Но ∂U/∂y=Q(x;y)=x-1/y. То есть x+φ'(y)=x-1/y, отсюда φ'(y)=-1/y. Интегрируем:
3) Так как U(x;y)=xy+φ(y), то U(x;y)=xy-ln│y│+C1. А поскольку интеграл уравнения в полных дифференциалах dU(x;y)=0 есть U(x;y)=C, то xy-ln│y│=С.
Уравнения в полных дифференциалах. Интегрирующий множитель
Дифференциальное уравнение первого порядка вида
называется уравнением в полных дифференциалах , если его левая часть представляет полный дифференциал некоторой функции , т.е.
Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области изменения переменных и выполнялось условие
Общий интеграл уравнения (1) имеет вид или
Пример 1. Решить дифференциальное уравнение .
Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах:
так что т.е. условие (2) выполнено. Таким образом, данное уравнение есть уравнение в полных дифференциалах и
поэтому , где пока неопределенная функция.
Интегрируя, получаем . Частная производная найденной функции должна равняться , что дает откуда так что Таким образом, .
Общий интеграл исходного дифференциального уравнения .
При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получаются легко интегрируемые комбинации.
Пример 2. Решить дифференциальное уравнение .
Решение. Здесь , так что условие (2) выполнено и, следовательно, данное уравнение есть уравнение в полных дифференциалах. Это уравнение легко привести к виду непосредственной группировкой его членов. С этой целью перепишем его так:
Поэтому изначальное уравнение можно записать в виде
Следовательно, есть общий интеграл исходного уравнения.
Интегрирующий множитель
В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функцию , после умножения на которую левая часть (1) превращается в полный дифференциал
Такая функция называется интегрирующим множителем . Из определения интегрирующего множителя имеем
Мы получили для нахождения интегрирующего множителя уравнение в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (5), т.е. найти интегрирующий множитель.
1. Если , то и уравнение (5) примет вид
Для существования интегрирующего множителя, не зависящего от , необходимо и достаточно, чтобы правая часть (6) была функцией только . В таком случае найдется квадратурой.
Пример 3. Решить уравнение .
Решение. Здесь . Имеем
Уравнение есть уравнение в полных дифференциалах. Его левую часть можно представить в виде
2. Аналогично, если есть функция только , то уравнение (1) имеет интегрирующий множитель , зависящий только от .
Пример 4. Решить уравнение .
Решение. Здесь . Имеем
Уравнение является уравнением в полных дифференциалах. Его можно записать в виде
Пример 5. Решить уравнение , если его интегрирующий множитель имеет вид .
Решение. Положим , тогда , и, следовательно,
Уравнение (5) для нахождения интегрирующего множителя будет иметь вид
и, значит, , откуда , т.е. . Умножая данное уравнение на , получим
Это есть уравнение в полных дифференциалах и его общий интеграл согласно (3) будет
После несложных преобразований будем иметь .
Проинтегрировать уравнение найдя интегрирующий множитель указанного вида
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |