Производная функции это уравнение рисунок функция

Определение, физический и геометрический смысл производной

п.1. Приращение аргумента и приращение функции

	\begin y=2x-1\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end
	\begin y=-x+2\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end

п.2. Определение производной

Например:
Найдем производную функции $f(x)=x^2-4$ в точке $x_0=3$
Значение функции в точке: $f(x_0 )=3^2-4=5$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда: \begin f(x)=f(x_0+\triangle x)=(x_0+\triangle x)^2-4=(3+\triangle x)^2-4=9+6\triangle x+\triangle x^2-4=\\ =5+6\triangle x+\triangle x^2 \end Приращение функции: $$ \triangle y=f(x)-f(x_0)=5+6\triangle x+\triangle x^2-5=6\triangle x+\triangle x^2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle y>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(6+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(6+\triangle x)=6+0=6 $$ Ответ: 6

п.3. Физический смысл производной

Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами $\triangle x=$ 300 км поезд преодолевает за $\triangle t=$4 часа. Мы легко можем найти его среднюю скорость: $$ v_=\frac<\triangle x><\triangle t>,\ \ v_=\frac<300><4>=75\ (\text<км/ч>) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.

Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:

Или, ближе к физике/химии/биологии:

п.4. Геометрический смысл производной

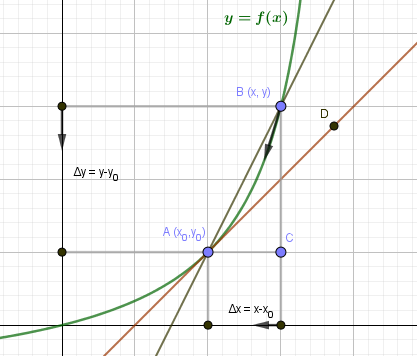
Пусть на плоскости задана кривая $y=f(x)$.
Выберем на кривой две точки $A(x_0,y_0)$ и $B(x,y)$. Прямая AB будет секущей для кривой $y=f(x)$. Угол наклона прямой AB определяется угловым коэффициентом: $$ k_=tg\angle A=\frac=\frac<\triangle y> <\triangle x>$$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: $\triangle x=AC\rightarrow 0$. В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_=\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:

п.5. Алгоритм поиска значения производной в заданной точке

На входе: уравнение функции $y=f(x)$, точка $x_0$
Шаг 1. Найти значение функции в заданной точке $y_0=f(x_0)$.
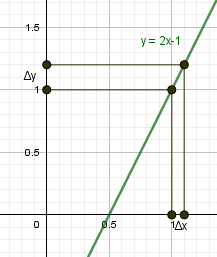
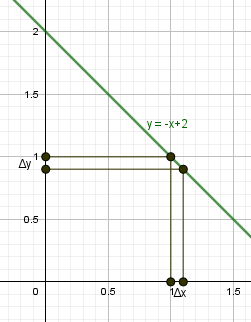
Шаг 2. Задать приращение аргумента $\triangle x=x-x_0$, найти приращение функции $\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)$.
Шаг 3. Найти предел $\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x_0)$
На выходе: значение производной в точке $x_0$

Например:
Найдем значение производной в точке $x_0=1$ для функции $y=x^2-3$.
Значение функции в заданной точке: $f(x_0)=1^2-3=-2$
Пусть $∆x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=((1+\triangle x)^2-3)-(-2)=\\ =1+2\triangle x+(\triangle x)^2-1=2\triangle x+(\triangle x)^2=\triangle x(2+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2+\triangle x)=2+0=2 \end Искомая производная в заданной точке: $f'(1)=2$
Ответ: 2

п.6. Алгоритм поиска уравнения производной

На входе: уравнение функции $y=f(x)$
Шаг 1. Задать приращение аргумента $\triangle x$, найти выражение для приращения функции $\triangle y=f(x+\triangle x)-f(x)$.
Шаг 2. Найти предел выражения $\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x)$
На выходе: уравнение производной $y\ ‘=f'(x)$ в любой точке $x$.

Например:
Найдем общее уравнение производной для функции $y=x^2-3$.
Пусть $∆x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=((x+\triangle x)^2-3)-(x^2-3)=\\ =(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Ответ: уравнение производной $y\ ‘=2x$

п.7. Примеры

Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) $ f'(1),\ \text<если>\ f(x)=2x $
По условию $x_0=1$
Значение функции в заданной точке: $f(x_0 )=2\cdot 1=2$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<2\triangle x><\triangle x>=2 \end Искомая производная в заданной точке: $f'(1)=2$
б) $ f'(3),\ \text<если>\ f(x)=3x^2 $
По условию $x_0=3$
Значение функции в заданной точке: $f(x_0 )=3\cdot 3^2=27$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=3(3+\triangle x)^2-27=3(9+6\triangle x+(\triangle x)^2)-27=\\ =27+18\triangle x+3(\triangle x)^2-27=3\triangle x(6+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<3\triangle x(6+\triangle x)><\triangle x>=3\lim_<\triangle x\rightarrow 0>(6+\triangle x)=3(6+0)=18 \end Искомая производная в заданной точке: $f'(3)=18$

в) $ f'(-1),\ \text<если>\ f(x)=4x-1 $
По условию $x_0=-1$
Значение функции в заданной точке: $f(x_0)=4\cdot (-1)-1=-5$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(4(-1+\triangle x)-1)-(-5)=-5+4\triangle x+5=4\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<4\triangle x><\triangle x>=4 \end Искомая производная в заданной точке: $f'(-1)=4$

г) $ f'(2),\ \text<если>\ f(x)=x^3 $
По условию $x_0=2$
Значение функции в заданной точке: $f(x_0)=2^3=8$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(2+\triangle x)^3-8=\\ =2^3+3\cdot 2^2\cdot \triangle x+3\cdot 2\cdot (\triangle x)^2+(\triangle x)^3-8=\\ =12\triangle x+6(\triangle x)^2+(\triangle x)^3=\triangle x\cdot (12+6\triangle x+(\triangle x)^2 ) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x\cdot(12+6\triangle x+(\triangle x)^2)><\triangle x>=\lim_<\triangle x\rightarrow 0>(12+6\triangle x+(\triangle x)^2)=12+0+0=12 \end Искомая производная в заданной точке: $f'(2)=12$

Ответ: а) 2; б) 18; в) 4; г) 12

Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции $y=f(x)$:
a) $ f(x)=C$, где C – постоянная величина
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end Отношение $\frac<\triangle y><\triangle x>=\frac<0><\triangle x>=0$
Предел $\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>0=0$
Производная $y\ ‘=C’=0$

б) $ f(x)=x$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end Ищем предел: $\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle x>=\lim_<\triangle x\rightarrow 0>1=1$
Производная $x\ ‘=1$

в) $ f(x)=x^2$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Производная $(x^2)\ ‘=2x$

г) $ f(x)=x^3$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^3-x^3=\\ =(x+\triangle x-x)((x+\triangle x)^2+x(x+\triangle x)+x^2)=\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2)><\triangle x>=\\ =\lim_<\triangle x\rightarrow 0>((x+\triangle x)^2+x(x+\triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 \end Производная $(x^3)\ ‘=3x^2$

e) $ f(x)=kx+b$
Пусть $\triangle x$ — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x>=\lim_<\triangle x\rightarrow 0>k=k \end Производная $(kx+b)\ ‘=k$

Производная функции. Геометрический смысл производной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку A с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

Величина в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.

В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».

В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

возрастает	точка максимума	убывает	точка минимума	возрастает
+	0	—	0	+

Ты нашел то, что искал? Поделись с друзьями!

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.

Н.С. Шернина, преподаватель Кубанского госуниверситета

1. Производная

Рассмотрим некоторую функцию в двух точках и : и .
Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: называется приращением функции.

Если этот предел существует, то функция называется дифференцируемой в точке . Производная функции обозначается (формула 2)

2. Геометрический смысл производной

Рассмотрим график функции .

Из рис.1 видно, что для любых двух точек A и B графика функции можно записать формула 3). В ней — угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует вывод.

3. Уравнение касательной

Выведем уравнение касательной к графику функции в точке . В общем случае уравнение прямой с угловым коэффициентом имеет вид:
Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:
Отсюда следует: .
Подставляя это выражение вместо b, получаем уравнение касательной(формула 4).

4. Механический смысл производной

Рассмотрим простейший случай: движение материальной точки вдоль координатной оси. При этом задан закон движения точки: координата x движущейся точки – это известная функция времени . В течение интервала времени от до точка перемещается на расстояние: .
Её средняя скорость () находится по формуле: . При значение средней скорости стремится к определённой величине, которая в физике называется мгновенной скоростью материальной точки в момент времени . Следовательно, для мгновенной скорости можно записать формулу 5

Если сравнить эту формулу с формулой производной 1, то можно сделать вывод, что

5. Дифференциал и его связь с производной
Дифференциал функции. Геометрический смысл дифференциала

Дифференциал функции – это произведение производной и приращения аргумента (формула 6).

Геометрический смысл дифференциала ясен из рисунка 2.

Здесь . Из можно записать: , где β – угол наклона касательной АС к оси ОХ. Но если , то . Дифференциал CD равен сумме отрезков BС и BD (приращение функции). Но, если , то и отрезок . Значит, дифференциал отличается от производной на бесконечно малую величину.

6. Основные свойства производных и дифференциалов. Производная сложной функции
6.1 Правила дифференцирования функций. Таблица производных простейших элементарных функций.
Если , то , .
Если и — дифференцируемые функции в точке , то можно записать:

Таблица производных простейших элементарных функций

1. ,
где С – постоянное число
2.
Частные случаи:

3.
Частный случай

4.
Частный случай

5.
6.
7.
8.
9.
10.
11.
12.

6.2 Производная сложной функции

Рассмотрим сложную функцию, аргумент которой также является функцией: . Если функция f имеет производную в точке , а функция g имеет производную в точке , то сложная функция h также имеет производную в точке , вычисляемую по формуле:

6.3 Вторая производная

Если производная функции дифференцируема в точке , то её производная называется второй производной функции в точке , и обозначается .

6.4 Правило Лопиталя

Пусть при для функций и, дифференцируемых в некоторой окрестности точки а , выполняются условия. (формулы 7).

Эта теорема называется правилом Лопиталя. Она позволяет вычислять пределы отношения функций, когда и числитель, и знаменатель cтремятся либо к нулю, либо к бесконечности. Правило Лопиталя, как говорят математики, позволяет избавляться от неопределённостей типа: и . Рассмотрите примеры.

При неопределённостях другого типа: , , , , нужно проделать предварительно ряд тождественных преобразований, чтобы привести их к какой-то из двух неопределённостей: либо , либо . После этого можно применять правило Лопиталя. Покажем некоторые из возможных преобразований указанных неопределённостей.

: пусть ,, тогда данная неопределённость приводится к типу посредством следующего преобразования:

: пусть , , тогда данная неопределённость приводится к типу или с помощью преобразований:

остальные неопределённости приводятся к первым двум с помощью логарифмического преобразования:

Если же после применения правила Лопиталя неопределённость типа или осталась, нужно применить его повторно. Многократное применение правила Лопиталя может привести к требуемому результату. Правило Лопиталя применимо и в случае, если .

7. Применение производной в исследовании функций
7.1 Связь между непрерывностью и дифференцируемостью функции

Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной (рисунок 3). Если же функция разрывная в некоторой точке, то она не имеет производной в этой точке.

7.2 Достаточные признаки монотонности функции

Если в каждой точке интервала , то функция возрастает на этом интервале. Если в каждой точке интервала , то функция убывает на этом интервале.

7.3 Теорема Дарбу

Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.Рассмотрите примеры

Следовательно, функция на рисунке 4а возрастает на интервалах и и убывает на интервале . Точка не входит в область определения функции, но по мере приближения x к 0 слагаемое неограниченно возрастает. Поэтому функция также неограниченно возрастает. В точке значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ).

7.4 Критические точки

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум, рис.5а,б).

В точках , (рис.5a) и (рис.5b) производная равна 0. В точках , (рис.5б) производная не существует. Но все они – это точки экстремума.

7.5 Необходимое условие экстремума

Если — точка экстремума функции и производная существует в этой точке, то .

Эта теорема – необходимое условие экстремума. Если же производная функции в некоторой точке равна 0, то это не значит, что функция всегда имеет экстремум в этой точке. Например, производная функции равна 0 при , но эта функция не имеет экстремум в этой точке ( рис.6 ).
С другой стороны, функция , представленная на рис.3, имеет минимум в точке , но в этой точке производной не существует.

7.6 Достаточные условия экстремума

Если производная при переходе через точку меняет свой знак с плюса на минус, то — точка максимума.
Если производная при переходе через точку меняет свой знак с минуса на плюс, то — точка минимума.

7.7 План исследования функции
Для построения графика функции нужно:

Пример . Исследование функции , построение графика
1) область определения (x – любое действительное число); область значений , так как – многочлен нечётной степени;
2) функция не является ни чётной, ни нечётной (докажите самостоятельно);
3) – непериодическая функция (докажите самостоятельно);
4) график функции пересекается с осью Y в точке , так как .
Чтобы найти нули функции нужно решить уравнение: .
Один из его корней очевиден. Другие корни находятся (если они есть!) из решения квадратного уравнения: . Оно получено делением многочлена на двучлен . Легко проверить, что два других корня: и . Таким образом, нулями функции являются:-2, -1 и 1.

5) Это означает, что числовая ось делится этими корнями на четыре интервала знакопостоянства, внутри которых функция сохраняет свой знак. Этот же результат может быть получен разложением многочлена на множители:
. Затем надо оценить знак произведения методом интервалов.
6) Производная не имеет точек, в которых она не существует, поэтому её область определения R (все действительные числа); нули – это корни уравнения: .
Эти корни: .
Функция имеет две критические точки и три интервала монотонности: .
Полученные результаты сведены в таблицу. В ней стрелками обозначены выводы о возрастании функции или её убывании (наклонная стрелка вверх или вниз) внутри соответствующего интервала.

Теперь мы располагаем полной информацией для построения графика данной функции (рис. 8).

7.8 Выпуклость, вогнутость, точки перегиба

Функция называется выпуклой на интервале , если её график на этом интервале лежит ниже касательной, проведенной к кривой в любой точке , при этом .
Функция называется вогнутой на интервале , если её график на этом интервале лежит выше касательной, проведенной к кривой в любой точке , при этом .

7.9 Достаточное условие вогнутости (выпуклости) функции

Пусть функция дважды дифференцируема (имеет вторую производную) на интервале , тогда: если для любого , то функция является вогнутой на интервале ; если для любого , то функция является выпуклой на интервале .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба существует вторая производная , то .
Пример : Рассмотрим график функции . Эта функция является вогнутой при и выпуклой при .
В самом деле, , но при и при , следовательно, при и при , откуда следует, что функция является вогнутой при и выпуклой при . Тогда является точкой перегиба функции .