Производная функции y f x уравнение

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Найти (с решением) производную функции.

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите выражение функции Найти производную функции f(x)

Немного теории.

Определение производной

Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac<\Delta y> <\Delta x>\). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).

Для обозначения производной часто используют символ \( y’ \). Отметим, что \( y’ = f(x) \) — это новая функция, но, естественно, связанная с функцией \( y = f(x) \), определенная во всех точках \(x\), в которых существует указанный выше предел. Эту функцию называют так: производная функции \( y = f(x) \).

Геометрический смысл производной состоит в следующем. Если к графику функции \( y = f(x) \) в точке с абсциссой \( x=a \) можно провести касательную, непараллельную оси \(y\), то \( f(a) \) выражает угловой коэффициент касательной:
\( k = f'(a) \)

Поскольку \( k = tg(a) \), то верно равенство \( f'(a) = tg(a) \) .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \( y = f(x) \) имеет производную в конкретной точке \( x \):
$$ \lim_ <\Delta x \to 0>\frac<\Delta y> <\Delta x>= f'(x) $$
Это означает, что около точки \(x\) выполняется приближенное равенство \( \frac<\Delta y> <\Delta x>\approx f'(x) \), т.е. \( \Delta y \approx f'(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке \(x\).
Например, для функции \( y = x^2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \( x \), найти \( f(x) \)
2. Дать аргументу \( x \) приращение \( \Delta x \), перейти в новую точку \( x+ \Delta x \), найти \( f(x+ \Delta x) \)
3. Найти приращение функции: \( \Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \( \frac<\Delta y> <\Delta x>\)
5. Вычислить $$ \lim_ <\Delta x \to 0>\frac<\Delta y> <\Delta x>$$
Этот предел и есть производная функции в точке \(x\).

Если функция \(y=f(x)\) имеет производную в точке \(x\), то ее называют дифференцируемой в точке \(x\). Процедуру нахождения производной функции \(y=f(x)\) называют дифференцированием функции \(y=f(x)\).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция \(y=f(x)\) дифференцируема в точке \(x\). Тогда к графику функции в точке \( M(x; \; f(x)) \) можно провести касательную, причем, напомним, угловой коэффициент касательной равен \( f'(x) \). Такой график не может «разрываться» в точке \(M\), т. е. функция обязана быть непрерывной в точке \(x\).

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция \(y=f(x)\) дифференцируема в точке \(x\), то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция \( y=|x|\) непрерывна везде, в частности в точке \(x=0\), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \( y=\sqrt[3] \) непрерывна на всей числовой прямой, в том числе в точке \(x=0\). И касательная к графику функции существует в любой точке, в том числе в точке \(x=0\). Но в этой точке касательная совпадает с осью \(y\), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид \(x=0\). Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если \(C\) — постоянное число и \( f=f(x), \; g=g(x) \) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

Пошаговый калькулятор производных онлайн

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Определение, физический и геометрический смысл производной

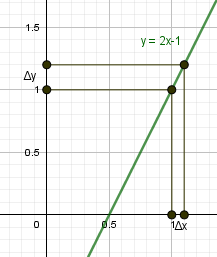
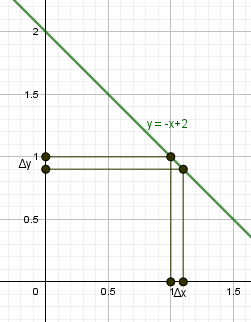
п.1. Приращение аргумента и приращение функции

	\begin y=2x-1\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end
	\begin y=-x+2\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end

п.2. Определение производной

Например:
Найдем производную функции \(f(x)=x^2-4\) в точке \(x_0=3\)
Значение функции в точке: \(f(x_0 )=3^2-4=5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда: \begin f(x)=f(x_0+\triangle x)=(x_0+\triangle x)^2-4=(3+\triangle x)^2-4=9+6\triangle x+\triangle x^2-4=\\ =5+6\triangle x+\triangle x^2 \end Приращение функции: $$ \triangle y=f(x)-f(x_0)=5+6\triangle x+\triangle x^2-5=6\triangle x+\triangle x^2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle y>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(6+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(6+\triangle x)=6+0=6 $$ Ответ: 6

п.3. Физический смысл производной

Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами \(\triangle x=\) 300 км поезд преодолевает за \(\triangle t=\)4 часа. Мы легко можем найти его среднюю скорость: $$ v_=\frac<\triangle x><\triangle t>,\ \ v_=\frac<300><4>=75\ (\text<км/ч>) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.

Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:

Или, ближе к физике/химии/биологии:

п.4. Геометрический смысл производной

Пусть на плоскости задана кривая \(y=f(x)\).
Выберем на кривой две точки \(A(x_0,y_0)\) и \(B(x,y)\). Прямая AB будет секущей для кривой \(y=f(x)\). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_=tg\angle A=\frac=\frac<\triangle y> <\triangle x>$$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: \(\triangle x=AC\rightarrow 0\). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_=\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:

п.5. Алгоритм поиска значения производной в заданной точке

На входе: уравнение функции \(y=f(x)\), точка \(x_0\)
Шаг 1. Найти значение функции в заданной точке \(y_0=f(x_0)\).
Шаг 2. Задать приращение аргумента \(\triangle x=x-x_0\), найти приращение функции \(\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)\).
Шаг 3. Найти предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x_0)\)
На выходе: значение производной в точке \(x_0\)

Например:
Найдем значение производной в точке \(x_0=1\) для функции \(y=x^2-3\).
Значение функции в заданной точке: \(f(x_0)=1^2-3=-2\)
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=((1+\triangle x)^2-3)-(-2)=\\ =1+2\triangle x+(\triangle x)^2-1=2\triangle x+(\triangle x)^2=\triangle x(2+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2+\triangle x)=2+0=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
Ответ: 2

п.6. Алгоритм поиска уравнения производной

На входе: уравнение функции \(y=f(x)\)
Шаг 1. Задать приращение аргумента \(\triangle x\), найти выражение для приращения функции \(\triangle y=f(x+\triangle x)-f(x)\).
Шаг 2. Найти предел выражения \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x)\)
На выходе: уравнение производной \(y\ ‘=f'(x)\) в любой точке \(x\).

Например:
Найдем общее уравнение производной для функции \(y=x^2-3\).
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=((x+\triangle x)^2-3)-(x^2-3)=\\ =(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Ответ: уравнение производной \(y\ ‘=2x\)

п.7. Примеры

Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) \( f'(1),\ \text<если>\ f(x)=2x \)
По условию \(x_0=1\)
Значение функции в заданной точке: \(f(x_0 )=2\cdot 1=2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<2\triangle x><\triangle x>=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
б) \( f'(3),\ \text<если>\ f(x)=3x^2 \)
По условию \(x_0=3\)
Значение функции в заданной точке: \(f(x_0 )=3\cdot 3^2=27\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=3(3+\triangle x)^2-27=3(9+6\triangle x+(\triangle x)^2)-27=\\ =27+18\triangle x+3(\triangle x)^2-27=3\triangle x(6+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<3\triangle x(6+\triangle x)><\triangle x>=3\lim_<\triangle x\rightarrow 0>(6+\triangle x)=3(6+0)=18 \end Искомая производная в заданной точке: \(f'(3)=18\)

в) \( f'(-1),\ \text<если>\ f(x)=4x-1 \)
По условию \(x_0=-1\)
Значение функции в заданной точке: \(f(x_0)=4\cdot (-1)-1=-5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(4(-1+\triangle x)-1)-(-5)=-5+4\triangle x+5=4\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<4\triangle x><\triangle x>=4 \end Искомая производная в заданной точке: \(f'(-1)=4\)

г) \( f'(2),\ \text<если>\ f(x)=x^3 \)
По условию \(x_0=2\)
Значение функции в заданной точке: \(f(x_0)=2^3=8\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(2+\triangle x)^3-8=\\ =2^3+3\cdot 2^2\cdot \triangle x+3\cdot 2\cdot (\triangle x)^2+(\triangle x)^3-8=\\ =12\triangle x+6(\triangle x)^2+(\triangle x)^3=\triangle x\cdot (12+6\triangle x+(\triangle x)^2 ) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x\cdot(12+6\triangle x+(\triangle x)^2)><\triangle x>=\lim_<\triangle x\rightarrow 0>(12+6\triangle x+(\triangle x)^2)=12+0+0=12 \end Искомая производная в заданной точке: \(f'(2)=12\)

Ответ: а) 2; б) 18; в) 4; г) 12

Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\):
a) \( f(x)=C\), где C – постоянная величина
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end Отношение \(\frac<\triangle y><\triangle x>=\frac<0><\triangle x>=0\)
Предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>0=0\)
Производная \(y\ ‘=C’=0\)

б) \( f(x)=x\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end Ищем предел: \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle x>=\lim_<\triangle x\rightarrow 0>1=1\)
Производная \(x\ ‘=1\)

в) \( f(x)=x^2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Производная \((x^2)\ ‘=2x\)

г) \( f(x)=x^3\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^3-x^3=\\ =(x+\triangle x-x)((x+\triangle x)^2+x(x+\triangle x)+x^2)=\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2)><\triangle x>=\\ =\lim_<\triangle x\rightarrow 0>((x+\triangle x)^2+x(x+\triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 \end Производная \((x^3)\ ‘=3x^2\)

e) \( f(x)=kx+b\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x>=\lim_<\triangle x\rightarrow 0>k=k \end Производная \((kx+b)\ ‘=k\)