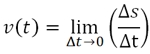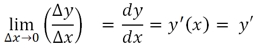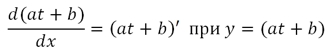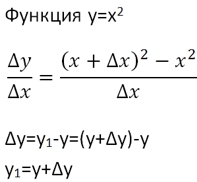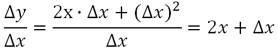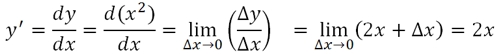Производная функция с квадратным уравнением

Квадратный трехчлен и его производная

Разделы: Математика

Класс: 11

Цели урока:

• Научить учащихся применять ранее полученные знания о квадратном трехчлене, линейной функции, производной, её геометрическом смысле в новой для них нестандартной ситуации;
• Показать учащимся при решении задач естественную неразрывную связь между алгеброй и геометрией.
• Формировать у учащихся навыки исследовательской работы.

Пособия:

• слайды презентации PowerPoint с чертежами к уроку.

План урока:

• Организационный момент;
• Объявление темы урока, постановка целей урока;
• Лекционное изложение нового материала с элементами закрепления:
• Закрепление материала практическим решением нестандартных задач.
• Итоги урока, постановка домашнего задания.

1. Организационный момент.

Приветствие учащихся. Сообщение темы, целей и плана урока.

2. Повторение свойств линейной и квадратичной функций;

По готовым слайдам презентации повторить свойства линейной и квадратичной функции.

3. Лекционная часть урока “Квадратный трехчлен и его производная”

Рассмотрим две функции: квадратный трехчлен и его производную , которая, очевидно, является линейной функцией. На рисунке 1 изображены их графики – парабола и прямая , которые иллюстрируют известный факт, что если на промежутке >0, то квадратный трехчлен на этом промежутке возрастает, если на промежутке ^ .

Касательная имеет вид . Чтобы найти нужно вычислить координаты точки А касания. Их нетрудно посчитать. Точка касания имеет координаты A, где . Составим уравнение касательной, зная угловой коэффициент и координаты точки касания, получим уравнение касательной . Это значит что . Теперь можно вычислить DF=. В прямоугольном треугольнике DCF острый угол равен углу между касательной и положительным направлением оси абсцисс, поэтому . Решая треугольник DCF находим СВ, а значит и искомое расстояние .

Задача 2. Как показано выше график квадратного трехчлена касается графика своей производной. Найдите координаты точки касания и докажите, что эта точка касания расположена всегда правее вершины параболы на одну единицу.

Решение. Координаты точки А касания посчитать нетрудно, А. Простой анализ координат точки А показывает, что абсцисса точки касания на единицу больше, чем абсцисса вершина параболы.

Задача 3. Парабола квадратного трехчлена и прямая , график его производной пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные с угловыми коэффициентами и. Докажите, что .

Решение. Абсциссы точек А и В пересечения параболы и прямой найдем из уравнения , , , ,

Найдем угловые коэффициенты и касательных, проведенные через точки А и В. Они равны значению функции в точках и , фактически эти значения совпадают с ординатами точек А и В. Вычислим их: , . Теперь ясно, что .

Еще один интересный момент. Если угловой коэффициент прямой АВ обозначить через , то учитывая, что , нетрудно установить удивительно простую зависимость между угловыми коэффициентами этих прямых: .

4. Практикум по решению задач.

Пусть некоторый квадратный трехчлен. Рассмотрим параболы и . Докажите, что вторая парабола получается из первой параллельным переносом на вектор .

Последовательность квадратных трехчленов, задана реккурентным соотношением , , . Докажите, что все параболы, являющиеся графиками функций из этой последовательности, имеют общую касательную.

Как продолжить последовательность функций из предыдущей задачи влево, если убрать ограничение , то есть найдите квадратный трехчлен, непосредственно предшествующий квадратному трехчлену.

Парабола пересекает ось

в двух точках. Через каждую из них проведены касательные, которые пересекаются в точке С. Найдите координаты точки С.

Ответы к задачам: 3. ; 4. .

5. Самостоятельная работа в двух вариантах.

Вариант 1. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что: медиана СМ треугольника АВС параллельна оси ординат;

Вариант 2. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что одна из средних линий треугольника АВС является касательной к параболе .

6. Разбор задач самостоятельной работы

Разбор проводится по заранее подготовленным слайдам презентации PowerPoint. Оба варианта рассматриваются одновременно, потому что первая часть решения задач обоих вариантов одинакова, вторая же, различная часть, будет интересна учащимся обоих вариантов.

7. Задание на дом:

Рассмотрим четыре параболы , , и , где – некоторый квадратный трехчлен. Докажите, что вершины этих парабол совпадают с вершинами некоторого квадрата.

Производная квадратичной функции

На странице «Производная функции» мы выяснили, что предел отношения Δs/Δt получил название производной функции s(t).

Напомним, что величина Δs — это приращение расстояния; Δt — приращение времени.

Определение производной можно сформулировать в следующем виде:

Производной называется предел отношения приращения расстояния к приращению времени, при стремлении к нулю последнего.

Если уйти от конкретики, и не привязываться к расстоянию и времени, то определение производной будет звучать так:

Производная — это предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной.

Смысл производной заключается в том, что она показывает скорость изменения функции при изменении её аргумента.

Напомним важные моменты производной для функции s(t):

• приращение независимой переменной может быть сколь угодно малым, но обязательно отличным от нуля;
• поскольку s есть функция t [s(t)], то и предел отношения Δs/Δt является также функцией t, которая называется мгновенной скоростью v(t);
• v зависит от значения t при котором берется производная s.

Обозначение производной через предел довольно громоздко и не совсем удобно, поэтому, чаще используют сокращенные варианты (в общем случае вместо переменной s используется перменная y, а вместо переменной t — переменная x — что вполне логично, поскольку расстояние мы откладывали по оси ординат, а время — по оси абсцисс):

Частенько вместо функции пишется ее выражение:

На странице Равноускоренное движение мы искали производную квадратичной функции «наощупь», пошагово уменьшая приращение времени, теперь сделаем это алгебраически.

Изначально составим соотношение:

Знаменатель не трогаем. В числителе делаем преобразования, чтобы избавиться от переменной y. Дэльта игрек — это разность между начальной точкой (y) и некой точкой (y₁), соответствующей величине приращения (y+Δy). После этого заменяем y на x 2 .

Раскрывая скобки в числителе, получаем выражение:

Теперь наше соотношение примет следующий вид:

Ищем предел квадратичной функции:

Последнее равенство требует пояснения. Предел двух слагаемых одно из которых независимо, а второе стремится к нулю, будет равен независимому слагаемому.

Алгебраическим путём мы нашли производную квадратичной функции (y=x 2 ):

Теперь ещё раз вернёмся на страницу Равноускоренного движения, на которой мы пошаговым путём нашли производную квадратичной функции для значений t=1 (s’=2) и t=2,5 (s’=5).

Подставляя эти же значения в нашу формулу, мы получим те же значения производных.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Примеры решения производных с ответами

Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения производных

Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.

Процесс нахождения производный называется дифференцированием.

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»219″ style=»vertical-align: -5px;» />
11. 0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»180″ style=»vertical-align: -5px;» />
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 

– производная суммы (разницы).

– производная произведения.

– производная частного.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Примеры решений производных

Задача

Найти производную функции

Решение

Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:

Ответ

Задание

Найти производную функции

Решение

Обозначим , где . Тогда, согласно правила вычисления производной сложной функции, получим:

Ответ

Задача

Найти производную функции при .

Решение

.
.

Ответ

.

Задача

Найти производную функции .

Решение

.
После приведения подобных членов получаем:
.

Ответ

Задача

Найти производную функции .

Решение

В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:

.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Задача

Найти производную функции .

Решение

Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.

Ответ

.

Задача

Найти производную функции .

Решение

По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.

Ответ

.