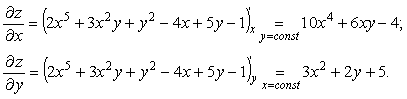Частные производные
Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2≡ z+(x-y)^(2/3)
Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
Пример 2 . Найти частные производные 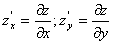
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:
Частные производные для функции от нескольких переменных
21 сентября 2015
Рассмотрим функцию от двух переменных:
\[f=f\left( x,y \right)\]
Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:
функции $f$ в точке $M=\left( <
_<0>>;< _<0>> \right)$ по переменной $x$ — это предел
Аналогично можно определить частную производную по переменной $y$ :
Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.
Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:
Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.
Что такое «частная производная»?
Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $y\left( x \right)$ или $t\left( x \right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.
Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.
Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.
Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $z\left( xy \right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.
На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.
Задачи с радикалами и многочленами
Задача № 1
Чтобы не терять время зря, с самого начала начнем с серьезных примеров.
Для начала напомню такую формулу:
Это стандартное табличное значение, которое мы знаем из стандартного курса.
В этом случае производная $z$ считается следующим образом:
Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $\frac
Возвращаемся к нашему выражению и записываем:
В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:
Ответ найден. Теперь займемся $y$:
Задача № 2
Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.
Приступаем к делу:
Однако многим ученикам такая запись непонятна, поэтому запишем вот так:
Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.
Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:
Подставим полученные выражения в нашу формулу и получим:
По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:
За счет симметрии мы посчитали это выражение гораздо быстрее.
Нюансы решения
Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».
Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:
Далее мы точно таким же образом считаем еще две конструкции, а именно:
Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:
Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.
Задачи с тригонометрическими функциями и логарифмами
Задача № 1
\[z\left( x,y \right)=\sqrt
Запишем следующие стандартные формулы:
Вооружившись этими знаниями, попробуем решить:
Отдельно выпишем одну переменную:
Возвращаемся к нашей конструкции:
Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:
Опять же посчитаем одно выражение:
Возвращаемся к исходному выражению и продолжаем решение:
Задача № 2
\[z\left( x,y \right)=\ln \left( x+\ln y \right)\]
Запишем необходимую нам формулу:
Теперь посчитаем по $x$:
По $x$ найдено. Считаем по $y$:
Нюансы решения
Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.
Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.
Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $\cos \frac
Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:
Задачи с показательными функциями и логарифмами
Задача № 1
Для начала запишем такую формулу:
Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:
Давайте решим отдельно следующее выражение:
Возвращаемся к нашей исходной конструкции и продолжаем решение:
Все, по $x$ посчитано.
Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:
В этом запишем так:
В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.
Теперь посчитаем по $y$:
Давайте решим одно выражение отдельно:
Продолжим решение нашей исходной конструкции:
Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.
Задача № 2
\[z\left( x,y \right)=x\ln \left( <
Давайте посчитаем одно выражение отдельно:
Продолжим решение исходной конструкции: $$
Вот такой ответ.
Осталось по аналогии найти по $y$:
Одно выражение посчитаем как всегда отдельно:
Продолжаем решение основной конструкции:
Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.
Нюансы решения
Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:
При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:
В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.
Задачи с тригонометрической функция и функцией с тремя переменными
Задача № 1
Давайте запишем такие формулы:
Давайте теперь решать наше выражение:
Отдельно посчитаем такую конструкцию:
Продолжаем решать исходное выражение:
Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:
Решим одно выражение отдельно:
Решаем до конца нашу конструкцию:
Задача № 2
На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.
Теперь разберемся с $y$:
Теперь остается найти по $z$:
Мы посчитали третью производную, на чем решение второй задачи полностью завершено.
Нюансы решения
Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.
В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.
Ключевые моменты
Окончательные выводы из сегодняшнего видеоурока следующие:
- Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
- При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.
Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!
Методическое пособие для преподавателей математики и студентов средних специальных учебных заведений. Частные производные. Дифференциальные уравнения в частных производных
Разделы: Математика
I Основные понятия функции нескольких переменных
1.1 Понятие функции нескольких переменных
Пусть D – некоторое множество пар действительных чисел и пусть каждой паре (x; y) из D поставлено в соответствие число Z. Тогда говорят, что на множестве D задана функция двух переменных Z = f(x,y).
Переменные x,y называют независимыми переменными (или аргументами), Z — зависимой переменной; говорят также, что f(x,y) есть значение функции f в точке (x;y).
Множество D называют областью определения функции.
Все значения, которые принимает функция f(x,y) (при (x,y) принадлежащих области её определения), образуют область значений функции.
Аналогично можно ввести понятие функции трех переменных u = f(x,y,z), определенной на множестве D, состоящем не из действительных чисел (как для функции одной переменной) и не из пар действительных чисел (как для функции двух переменных), а из троек действительных чисел (x,y,z), рассматриваемых в определенном порядке. Можно ввести понятие функции четырех, пяти и вообще любого конечного числа переменных – все такие функции называют функциями нескольких переменных.
Примеры функций нескольких переменных:
S = xy – площадь прямоугольника со сторонами x, y есть функция двух переменных;
U = IR (закон Ома) – напряжение U на участке электрической цепи есть функция двух переменных: силы тока I и сопротивления R;
V = xyz — объем прямоугольного параллелепипеда со сторонами x,y,z есть функция трех переменных.
Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции.
Наиболее употребительным (как и в случае функций одной переменной) является способ задания функции с помощью формулы Z = f(x,y), где f(x,y) – некоторое выражение с переменными x,y. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Значение функции Z = f(x,y) в точке M(x0,y0) называется частным значением функции и обозначается f(x0,y0) или f(M).
Дана функция Вычислить
1.2 Область определения
Область определения функции Z = f(x,y)в простейших случаях представляет собой либо часть плоскости, ограниченную замкнутой кривой, причем точки этой кривой (границы области) могут принадлежать или не принадлежать области определения, либо всю плоскость, либо, наконец, совокупность нескольких частей плоскости xOy
Геометрическим изображением функции Z = f(x,y) в прямоугольной системе координат Oxyz (графиком функции) является некоторая плоскость.
Для аналитически заданной функции иногда не указывают явно область ее определения. В таком случае подразумевают, что область определения функции Z = f(x,y) совпадает с областью определения выражения Z = f(x,y), т.е. с множеством тех значений x,y, при которых выражение f(x,y) имеет смысл.
Пример: Найти область определения функции:
а) Функция не определена лишь в случае, когда y = x. Геометрически это означает, что область определения функции состоит из двух полуплоскостей, одна из которых лежит выше, а другая ниже прямой y = x.
б) Функция определена при условии , т.е. . Это круг с центром в начале координат и радиусом

= 1.
в) Функция определена при условии — 4 > 0, т.е.
> 4. Это часть плоскости, лежащая вне круга с центром в начале координат и радиусом 2, не включающая границу круга, т.е. окружность
= 4
г) Функция определена при (x,y,z), удовлетворяющих одновременно условиям x 0, y
0, z
0.
1.3 Частные производные
Пусть задана функция Z = f(x,y).
Переменной x дадим приращение dx, а y оставим без изменения. Если существует предел:
то он называется частной производной от функции Z = f(x,y) по переменной x.
Обозначать частную производную от функции Z = f(x,y) по переменной x можно любым из символов:
Чтобы найти частную производную от функции Z = f(x,y) по переменной x, нужно найти производную от этой функции по x, считая, что x является постоянной.
Аналогично, частной производной от функции Z = f(x,y) по переменной y, называется предел:
и обозначается одним из символов:
Частная производная от функции Z = f(x,y) по переменной y — это производная от функции Z = f(x,y) по переменной 
Частные производные от функции нескольких переменных находятся как производные от функции одной переменной при условии, что все остальные переменные считаются на момент дифференцирования постоянными.
Частными производными второго порядка от функции Z = f(x,y) называются частные производные от частных производных первого порядка:
Частные производныеназываются смешанными частными производными второго порядка.
В точках, где смешанные производные непрерывны, они равны, т.е.:
Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1. Найти
.
Рассматривая y как постоянную величину, получим
Рассматривая x как постоянную, найдем
Пример 3. Найти
Найдем частные производные:
Дифференцируя повторно, получим
Пример 4.
.
Пример 6. Требуется показать, что функция удовлетворяет равенству:
Найдем частные производные первого порядка
Найдем смешанную производную
Подставим найденные производные в равенство
т.е. равенство верно.
Ответ: Функция удовлетворяет равенству
.
http://www.berdov.com/works/proizvodnaya/chastnie-proizvodnie/
http://urok.1sept.ru/articles/413219
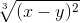 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)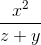 ≡ x^2/(z+y)
≡ x^2/(z+y) 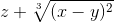 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)