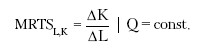Производственная функция фирмы имеет вид уравнение изокосты

Производственная функция Кобба-Дугласа. Изокванты и изокосты

Факторы производства и производственная функция

В современном мире нам не удастся выжить, орудуя одной лишь «палкой-копалкой», верно служившей нашим далёким предкам. Стол, кресло, компьютер, одежда, посуда, — всё стало настолько сложным, что одному человеку никак не справиться, и одновременно настолько простым, что десятки тысяч этих товаров каждую секунду сходят с конвейеров по всему миру.

Чтобы произвести что-нибудь, нужны ресурсы: сырьё, материалы, оборудование, энергия, информация, деньги, труд людей.

Факторы производства – это используемые в процессе производства ресурсы.

В простейшей модели производства рассматривают два основных фактора:

Результат производства – это некоторое количество Q выпущенного продукта.

Производственная функция – это зависимость количества выпущенного продукта от величины затрат факторов производства:

Пусть $Q = 1,5 \sqrt$.

Тогда при затратах K = 100 ед. капитала и L = 16 ед. труда, будет получено $Q = 1,5 \cdot \sqrt <100 \cdot 16>= 1,5 \cdot 10 \cdot 4 = 60$ ед. продукции.

Степенная производственная функция Кобба-Дугласа

Производственные функции можно строить по-разному.

Часто используется модель, в которой оба фактора – труд и капитал – входят в виде произведения степеней:

где A – технологический коэффициент (зависит от применяемой технологии);

$0 \le a \le 1$ — коэффициент эластичности.

Такие производственные функции называют функциями Кобба-Дугласа в честь американских исследователей, которые получили:

в 1927 году для обрабатывающей промышленности США.

Свойства производственной функции Кобба-Дугласа:

1. Если K = 0 или L = 0, то Q = 0, т.е. производство невозможно при отсутствии хотя бы одного фактора производства.

2. При увеличении затрат фактора производства, величина выпуска продукции возрастает: $K \uparrow \Rightarrow Q \uparrow, L \uparrow \Rightarrow Q \uparrow$

Тогда при затратах K=81 ед. капитала и L=16 ед. труда, будет получено $Q = 2,5 \cdot \sqrt[4] <81 \cdot 16^3>= 2,5 \cdot 3 \cdot 8 = 60$ ед. продукции.

Изокванты – линии равного выпуска

Пусть предприятие планирует выпустить $Q_0$ единиц продукции.

В этом случае, мы можем найти зависимость затрат капитала от затрат труда.

Эту зависимость можно изобразить на плоскости LOK в виде кривой.

Для каждого плана выпуска будет отдельная кривая.

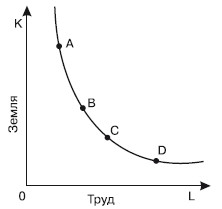
Множество точек (L;K) на плоскости LOK, которые соответствуют одному плану выпуска, называют изоквантой или линией равного выпуска .

Построим изокванты для $Q_0 = \<25;50;75;100 \>$ единиц готовой продукции.

1. Чем больше используется труда, тем меньше нужно капитала для производства заданного количества продукции. И наоборот: чем меньше труда, тем больше капитала. Труд и капитал взаимно заменяют друг друга.

2. Через каждую точку (L;K) проходит единственная изокванта.

3. Изокванты, соответствующие разным количествам продукции $Q_1 \neq Q_2$, не пересекаются.

Изокосты – линии равной стоимости

Согласно полученному выше графику, произвести $Q_0$ = 100 единиц продукции можно потратить 50 единиц труда и 20 единиц капитала, или же по 40 единиц труда и капитала, или же множество других сочетаний L и K.

Как нам определить, какое из сочетаний будет самым удачным? Очевидно, исходя из цены каждого ресурса. Пусть r — цена единицы капитала, а w – цена единицы труда. Тогда для некоторого набора ресурсов (L,K ), их общая стоимость:

На плоскости LOK это будет прямая с угловым коэффициентом $k = -\frac$.

Множество точек (L;K) на плоскости LOK, которые соответствуют одной величине затрат на ресурсы (бюджету), называют изокостой или линией равной стоимости .

Пусть цена ресурсов r = 5, w = 3.

Построим изокосты для общей суммы затрат C =

$$ \frac = \frac<3> <5>= 0,6, \frac = \frac <5>= 0,2C, K = -0,6L+0,2C $$

1. Угловой коэффициент изокосты равен отношению цен на ресурсы $k = -\frac$.

2. Изокоста для данного бюджета затрат C проходит через точки $(\frac,0)$ и $(0;\frac)$.

3. Для заданных цен на ресурсы изокосты для $C_1 \neq C_2$ являются параллельными прямыми.

План производства с минимальными затратами на ресурсы

Теперь поставим главную задачу:

При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, найти такое сочетание труда L и капитала K, при котором затраты на эти ресурсы минимальны:

$$ <\left\< \begin Q_0 = A \cdot K^a L^ <1-a>\\ C = wL+rK \rightarrow min \end \right.> $$

При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, затраты на ресурсы будут минимальными в точке $(L_0,K_0)$, в которой изокоста $C_0 (L_0,K_0)$ является касательной для изокванты $Q_0 (K,L)$, т.е. имеет с ней только одну общую точку.

Величина затрат для оптимальной изокванты:

Оптимальный объем ресурсов:

Пусть $Q = 2,5 \cdot K^\frac<1> <4>L^\frac<3><4>$. План выпуска продукции $Q_0 = 100$ единиц.

Цена ресурсов r = 5, w = 3.

Найти оптимальное отношение труда к капиталу $\frac$, при котором затраты на ресурсы будут минимальными.

$$ = 40 \cdot 2^2 \cdot \sqrt[4] <5>= 160 \sqrt[4] <5>$$

Оптимальный объем ресурсов:

Объем труда в 5 раз больше объема капитала при оптимальных затратах.

В плоскости LOK:

Таким образом, точка $(40 \sqrt[4]<5>;8 \sqrt[4]<5>)$ является точкой касания изокосты с минимальным бюджетом затрат $C_0 = 160 \sqrt[4]<5>$ и изокванты с планом выпуска $Q_0 = 100$.

Изокванта и изокоста. Равновесие производителя. Отдача от масштаба

ИЗОКВАНТА – кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска.

Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе. При этом увеличение одного фактора и уменьшение другого не вызывают изменений в объеме выпускаемой продукции. Данная зависимость изображена на рис. 21.1.

Положительный наклон изокванты означает, что увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора.

Изокванты выпуклы в направлении начала координат, поскольку хотя факторы могут быть заменяемы один другим, однако они не являются абсолютными заменителями.

Кривизна изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и отражает то, насколько легко один фактор может быть заменен другим. В том случае, когда изокванта похожа на прямой угол, вероятность замещения одного фактора другим крайне невелика. Если же изокванта имеет вид прямой линии с наклоном вниз, то вероятность замены одного фактора другим значительна.

Изокванты схожи с кривыми безразличия с той лишь разницей, что кривые безразличия выражают положение в сфере потребления, а изокванты – в сфере производства. Другими словами, кривые безразличия характеризуют замену одного блага другим (MRS), а изокванты – замену одного фактора другим (MRTS).

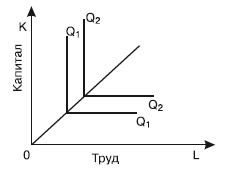
Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Крутизна наклона изокванты выражает предельную норму технического замещения (MRTS), которая измеряется соотношением изменения объема выпуска продукции. Предельная норма технического замещения трудом капитала (MRTS_LK) определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объема выпуска продукции. Предельная норма технического замещения в любой точке изокванты равна наклону касательной в этой точке, умноженному на -1:

Изокванты могут иметь различную конфигурацию: линейную, жесткой дополняемости, непрерывной замещаемости, ломаной изокванты. Здесь выделим две первые.

Линейная изокванта – изокванта, выражающая совершенную замещаемость факторов производства (MRTS_LK = const) (рис. 21.2).

Рис. 21.2. Линейная изокванта

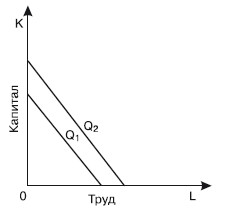
Жесткая дополняемость факторов производства представляет такую ситуацию, при которой труд и капитал сочетаются в единственно возможном соотношении, когда предельная норма технического замещения равна нулю (MRTS_LK = 0), так называемая изокванта леонтьевского типа (рис. 21.3).

Рис. 21.3. Жесткая изокванта

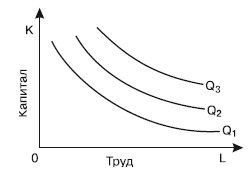
Карта изоквант представляет собой набор изоквант, каждая из которых иллюстрирует максимально допустимый объем производства продукции при любом данном наборе факторов производства. Карта изоквант является альтернативным способом изображения производственной функции.

Смысл карты изоквант аналогичен смыслу карты кривых безразличия для потребителей. Карта изоквант схожа с контурной картой горы: все большие высоты показаны посредством кривых (рис. 21.4).

Карта изоквант может быть использована для того, чтобы показать возможности выбора среди множества вариантов организации производства в рамках короткого периода, когда, например, капитал является постоянным фактором, а труд – переменным фактором.

Рис. 21.4. Карта изоквант

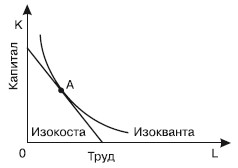
ИЗОКОСТА – линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег. Изокосту иначе называют линией равных издержек. Изокосты являются параллельными прямыми, поскольку допускается, что фирма может приобрести любое желаемое количество факторов производства по неизменным ценам. Наклон изокосты выражает относительные цены факторов производства (рис. 21.5). На рис. 21.5 каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Эти линии прямые, поскольку факторные цены имеют отрицательный наклон и параллельны.

Рис. 21.5. Изокоста и изокванта

Совместив изокванты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается (но не пересекает) изокосты, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного объема продукта (рис. 21.5). На рис. 21.5 показан метод определения точки, в которой минимизируются издержки производства заданного объема производства продукта. Эта точка расположена на самой нижней изокосте, где изокванта соприкасается с ней.

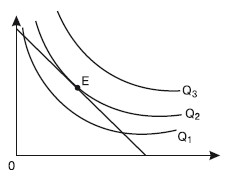
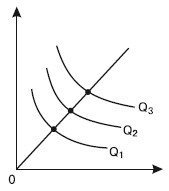
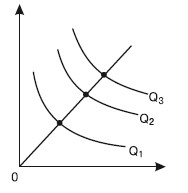
РАВНОВЕСИЕ ПРОИЗВОДИТЕЛЯ – состояние производства, при котором использование факторов производства позволяет получить максимальный объем продукции, т. е. когда изокванта занимает самую отдаленную от начала координат точку. Чтобы определить равновесие производителя, необходимо совместить карты изоквант с картой изокост. Максимальный объем выпуска будет в точке касания изокванты с изокостой (рис. 21.6).

Рис. 21.6. Равновесие производителя

Из рис. 21.6 видно, что изокванта, расположенная ближе к началу координат, дает меньшее количество производимой продукции (изокванта 1). Изокванты, расположенные выше и правее изокванты 2, вызовут изменение большего объема факторов производства, нежели позволяет бюджетное ограничение производителя.

Таким образом, точка касания изокванты и изокосты (на рис. 21.6 точка Е) является оптимальной, поскольку в этом случае производитель получает максимальный результат.

ОТДАЧА ОТ МАСШТАБА выражает реакцию объема производства продукции на пропорциональное изменение количества всех факторов производства.

Различают три положения отдачи от масштаба.

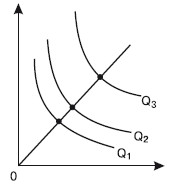
Возрастающая отдача от масштаба – положение, при котором пропорциональное увеличение всех факторов произволства приводит ко все большему увеличению объема выпуска продукта (рис. 21.7). Предположим, что все факторы производства увеличились в два раза, а объем выпуска продукта увеличился в три раза. Возрастающая отдача от масштаба обусловлена двумя основными причинами. Во-первых, повышением производительности факторов вследствие специализации и разделения труда при росте масштаба производства. Во-вторых, увеличение масштаба производства зачастую не требует пропорционального увеличения всех факторов производства. Например, увеличение вдвое производства цилиндрического оборудования (такого, как трубы) потребует увеличения металла меньше чем вдвое.

Постоянная отдача от масштаба – это изменение количества всех факторов производства, которое вызывает пропорциональное изменение объема выпуска продукта. Так, вдвое большее количество факторов ровно вдвое увеличивает объем выпуска продукта (рис. 21.8).

Убывающая отдача от масштаба – это ситуация, при которой сбалансированный рост объема всех факторов производства приводит ко все меньшему росту объема выпуска продукта. Иначе говоря, объем выпускаемой продукции увеличивается в меньшей степени, чем затраты факторов производства (рис. 21.9). Например, все факторы производства увеличились в три раза, а объем производства продукции – только в два раза.

Рис. 21.7. Возрастающая отдача от масштаба

Рис. 21.8. Постоянная отдача от масштаба

Рис. 21.9. Убывающая отдача от масштаба

Таким образом, в производственном процессе имеют место возрастающая, постоянная и убывающая отдачи от масштаба производства, когда пропорциональное увеличение количества всех факторов приводит к увеличившемуся, постоянному или убывающему приросту объема выпуска продукта.

Западные экономисты считают, что в настоящее время в большинстве видов производственной деятельности достигается постоянная отдача от масштаба. Во многих отраслях экономики возрастающая отдача от масштаба потенциально значима, однако с некоторого момента она может смениться убывающей отдачей, если не будет преодолен процесс увеличения числа гигантских фирм, что затрудняет управление и контроль, несмотря на то что технология производства стимулирует создание таких фирм.

Примеры решений задач: производственная функция

Производственная функция — экономико-математическая количественная зависимость между величиной выпуска (объемом продукции фирмы) и факторами производства, такими как затраты ресурсов, уровень технологий.

Наиболее известные примеры производственных функций: функция Кобба-Дугласа вида $Y=A\cdot L^<\alpha>\cdot K^<\beta>$, в которой предполагается постоянные эластичности ($\alpha$ и $\beta$) выпуска по факторам производства $K$ и $L$ соответственно (капитал и трудовые затраты); линейная производственная функция: $Y=aK+bL$, функция Леонтьева и т.д.

В этом разделе вы найдете подробно решенные задачи, касающиеся производственной функции (в том числе модели Кобба-Дугласа).

Производственная функция: задачи с решениями

Задача 1. Производственная функция коммерческого предприятия имеет вид $f=10\sqrt\cdot \sqrt$, где $f$ — товарооборот, тыс. руб.; $x_1$ — производственная площадь, м ; $x_2$ — численность работников, сотни человек. Рассмотрите изокванту уровня $y_0$ и найдите точку $C_1$ и точку $C_2$. Сделайте вывод о возможности замены ресурсов. Полученные результаты изобразите графически.

Задача 2. Исходные данные. Фирма, производящая продукцию при заданной рынком системе цен по технологии, отображающейся производственной функцией $Q = 20 L^<0,5>$, может продавать любой объем своей продукции по цене Р = 6. Фирма может использовать любое количество труда по цене w = 40.
1. Какой тип производственной функции представлен в задании? В чем ее особенность? Приведите пример подобного производства. Изобразите график заданной производственной функции, а также графики среднего и предельного продуктов переменного фактора (труда).
2. На основе представленных данных выведите функции общих, средних и предельных затрат фирмы, функцию индивидуального предложения фирмы и определите объем предложения при заданной цене блага.
3. Дайте характеристику статуса фирмы на товарном и факторном рынках в представленном примере. Раскройте различия в поведении фирмы-совершенного конкурента и фирмы-монопсониста на рынке фактора. Приведите примеры подобного поведения фирм на рынке труда.
4. Выведите функцию спроса фирмы на труд, если цена блага P = 6 и остается неизменной. Определите объем спроса на труд при w = 40. Решение сопроводите графиком. Укажите несколько факторов (не менее трех), влияющих на спрос фирмы на труд.

Задача 3. Процесс производства некоторого товара описывается с помощью производственной функции $q=f(x_1, x_2)=54x_1^<1/2>x_2^<2/3>$. Для плана (2,5) найти первый второй предельные продукты. Дайте экономическую интерпретацию полученным результатам. Выясните, характеризуется ли ПФ той или иной разновидностью эффекта масштаба. Предполагая, что производитель приобретает ресурсы по ценам (2,7) найдите функцию переменных издержек $C_v(q)$.

Модель Кобба-Дугласа: задачи с решениями

Задача 4. Производственная функция фирмы имеет вид: $Q = К^<0,5>\cdot L^<0,5>$. Предположим, что в день затрачивается 4 часа труда (L = 4) и 4 часа работы машин (К = 4).
Определить:
1) максимальное количество выпускаемой продукции;
2) средний продукт труда;
3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?

Задача 5. Задана производственная функция Кобба-Дугласа
Изобразить изокванту, соответствующую плану (36,27). Какое количество продукта выпускается при этом плане?
Найти первый, второй предельные продукты для плана (36,27) и дать экономическую интерпретацию полученным результатам.
Каким эффектом от расширения масштабов производства характеризуется производственная функция
Каковы затраты производителя на покупку ресурсов при плане производства (36,27) и заданном векторе цен на ресурсы (3,4)?
Найти самый дешевый (оптимальный) план по ресурсам, обеспечивающий выпуск такого же количества продукции, что и для плана (36,27). Найти аналитически решение этой задачи
методом Лагранжа
методом подстановки.
Сделать геометрическую иллюстрацию решения задачи, изобразив ОДР и целевую функцию линиями уровня.

Задача 6. На основании представленных в таблице ниже данных построить ПФ типа Кобба-Дугласа. Сделать прогноз объема производства отрасли на 2000 год, если планируются увеличение основных фондов на 20% и одновременное уменьшение трудовых ресурсов на 5% относительно предыдущего года. Пусть заданы агрегированные основные показатели некоторой отрасли за четыре года:

Задача 7. Для построенной в самостоятельной работе производственной функции рассчитать предельные производительности, предельные нормы замещения ресурсов в 1993 и 1999 годах, сделать сравнительный экономический анализ. При расчетах предположить, что ресурсы в исследуемом году заданы, объем производства вычисляется.

Задача 8. Пусть производственная функция имеет вид $Y = 0.94 \cdot K^<1.17>\cdot L^<1.57>$. Для базового года $K_0 = 727$ млн ден. ед., $L_0 = 97.7$ тыс. человек. Для отчётного года $K_1 = 977$ млн ден. ед., $L_1 = 127.7$ тыс. человек. Подсчитать индексы изменения характеристик, масштаб и экономическую эффективность производства. Дать экономическую интерпретацию.

Задача 9. Производственная функция фирмы, выпускающая линолеум, имеет вид $Y=177 K^ <0.356>L^<0.644>$. Здесь $Y$ – сотни м*м, $K$ – тыс. ден. ед., $L$ – сотня рабочих (сот. р.).
Стоимость ресурсов W=5,13 тыс. ден. ед./сот. раб.
q = 10 тыс. ден. ед./тыс. ден. ед.
Издержки производства ограничены суммой C = 1770 тыс. ден. ед.
Найти максимальный выпуск продукции, оптимальное количество рабочих и стоимость капитальных фондов.
Построить график изокванты и изокосты. Отметить оптимальную точку.
Оценить, как изменится выпуск продукции, если:
а) увеличить заработную плату на 8%;
б) уменьшить цену на фонды в два раза;
в) ввести дополнительные инвестиции в производство в количестве 57,7 тыс. ден. ед.

Задача 10. Найти объем продукции, произведенной за период $[0;52]$, если функция Кобба-Дугласа имеет вид: $f(t)=(364+7t)e ^<1/104 t>$

Задача 11. 1. Выпуск продукции фирмой описывается функцией Кобба-Дугласа $Y=AK^<\alpha>L^<1-\alpha>$. Ставка заработной платы равна $p_L$, норма процента на используемый капитал — $p_K$.
2. По заданному уровню выпуска продукции $Y$ определить объемы факторов $K$ и $L$, при которых общие издержки будут минимальны, и величину этих издержек.
3. По известной величине общих издержек $TC$ определить объем факторов $K$ и $L$, обеспечивающие максимальный выпуск продукции, и соответствующий объем выпуска.

Задача 12. На основании следующих данных построить производственную функцию Кобба-Дугласа.
Здесь $Y_i$ — производственный национальный доход (млрд. руб.), $K_i$ — среднегодовые основные производственные фонды (млрд. руб.), $L_i$ — среднегодовая численность занятых в материальном производстве (млн. чел.). Имеется прогноз на 1997 год: основных производственных фондов $K_<1996>\cdot N$ млн. руб. и трудовых ресурсов $L_<1996>\cdot N$, где $N$ (номер) млн. чел. На основании полученной производственной функции сделать точечный прогноз национального дохода на 1997 год.

Задача 13. Производственная функция задается формулой $Q = 150 K^<0,9>L^<0,5>$, где Q — выпуск, K – капитал, L — труд.
Найти:
a) Предельные продукты труда и капитала при K=16, L=125.
б) Коэффициенты эластичности выпуска по труду и капиталу и объяснить их экономический смысл для полученных значений.