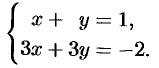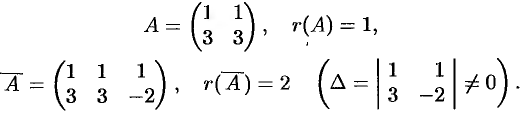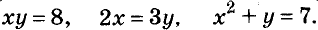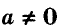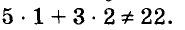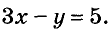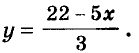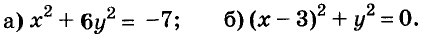Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа
Метод Лагранжа (вариация постоянных)
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1) .
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка, также применим и для уравнений более высоких порядков.
Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.
Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений. Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.
Шаг 1. Решение однородного уравнения
Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2) .
Общее решение такого уравнения имеет вид:
(3) .
Здесь – произвольные постоянные; – n линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.
Шаг 2. Вариация постоянных – замена постоянных функциями
На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x :
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4) .
Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n функций . При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n уравнений, из которых можно определить n функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций . Продемонстрируем это.
Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы и произведения:
.
Сгруппируем члены. Сначала выпишем члены с производными от , а затем – члены с производными от :
.
Наложим на функции первое условие:
(5.1) .
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1) .
Тем же способом находим вторую производную:
.
Наложим на функции второе условие:
(5.2) .
Тогда
(6.2) .
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций , к нулю.
Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k) ,
то первые производных по будут иметь наиболее простой вид:
(6.k) .
Здесь .
Подставляем в исходное уравнение (1):
(1) ;
.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7) .
В результате мы получили систему линейных уравнений для производных :
(5.1) ;
(5.2) ;
(5.3) ;
. . . . . . .
(5.n-1) ;
(7′) .
Решая эту систему, находим выражения для производных как функции от x . Интегрируя, получим:
.
Здесь – уже не зависящие от x постоянные. Подставляя в (4), получаем общее решение исходного уравнения.
Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты ai являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения (2).
Далее рассмотрены примеры решения уравнений методом Лагранжа.
Примеры
Решить уравнения методом вариации постоянных (Лагранжа).
Решение примеров > > >
Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 22-06-2017
Решение систем линейных уравнений
Решение систем линейных уравнений. Теорема Кронекера-Капелли
Пусть дана произвольная система 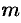
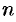
Исчерпывающий ответ па вопрос о совместности этой системы дает теорема Кронекера-Капелла.
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений
- Найти ранги основной и расширенной матриц системы. Если
, то система несовместна.
- Если
, система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять
уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные
неизвестных называют свободными и переносят в правые части уравнений.
- Найти выражения главных неизвестных через свободные. Получено общее решение системы.
- Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример №4.1.
Исследовать на совместность систему
Решение:
Таким образом, 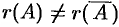
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
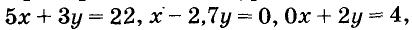
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 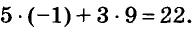
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 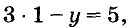
Уравнение 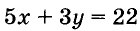
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 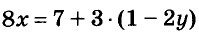
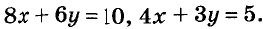
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 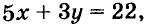
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 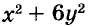
б) Значение выражения 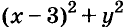
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 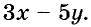
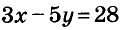
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 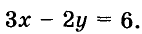
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://lfirmal.com/reshenie-sistem-linejnyih-uravnenij/
http://www.evkova.org/sistemyi-linejnyih-uravnenij

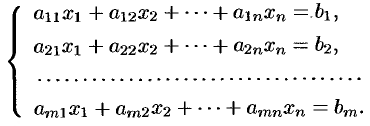
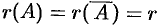 , система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять
, система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять 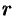 уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные
уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные 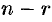 неизвестных называют свободными и переносят в правые части уравнений.
неизвестных называют свободными и переносят в правые части уравнений.