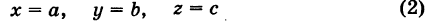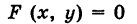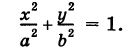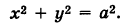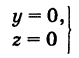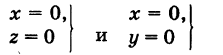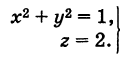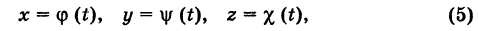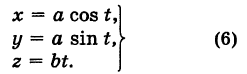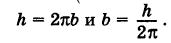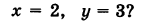Простейшие поверхности и их уравнения

Поверхности и линии в пространстве и их уравнения

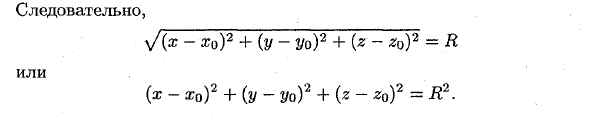
Поверхности и линии в пространстве и их уравнения

• ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ И ИХ УРАВНЕНИЯ 1. Поверхность и ее уравнение. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке 0 \ есть геометрическое место всех точек пространства, находящихся от точки 0 \ на расстоянии R. Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и г -. Их координаты Свойства, общая все точки поверхности, можно записать в виде уравнения, связывающая координата всех точек поверхности.

которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой Поверхностные координаты, точки и z в уравнении Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение Р (х, у, г) = 0 с тремя переменными х, у и г, Людмила Фирмаль

И не удовлетворяю Если центр сферы 0 \ соответствует точке начала координат, то уравнение сферы принимает вид х2 -4у2 4-2 -4у Если такое же дано уравнение вида F (x; у; z) = 0, то оно, вообще говоря, определяется в пространскопне Выражение «вообще говоря» означает, что в отдельных случаях уравнение F (х \ у \ г) = 0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ.

Примеры решения и задачи с методическими указаниями

• Говорят, «поверхность вырождается». . Так, уравнению 2х2 + у1 4- z2 4-1 = 0 не удовлетворяют никакие действительные значения гг, у, г Уравнению 0 • х2 4- у2 + z2 = 0 удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: 2 / = 0, z = 0, а ж-любое число). Итак, поверхность в пространстве может быть геометрической и аналитической. 1. Уравнение этой поверхности. 2. Дано уравнение F (x \ y \ z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве Fx (x-y \ z) = b F2 (x; y> z) = 0 Геометрия и геометрия Fx (x \ y \ z) = 0, F3 (®; y; *) = 0.Уравнение системы (1) 1-2 = 0

= О — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными Людмила Фирмаль

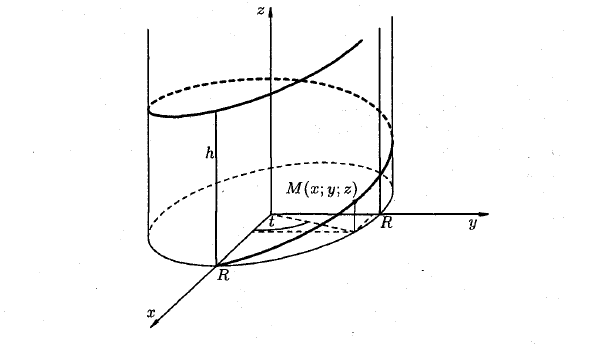
Траектории движения точки. (2) M (x \ y \ z) f = r (t) или параметрическими уравнениями х = х (т), У = 2 / (*), г = z (т) проекциями (2) на оси координат. Например, параметрические уравнения х = Я стоимость, у-R sin t, * = Если точка М равномерно двигается по образующей круговой цилиндру, а сам цилиндр равномерно вращается вокруг оси, то точка М описывает винтовая линия.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Уравнения поверхности и линии в пространстве

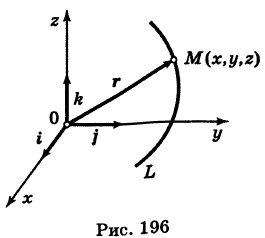
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

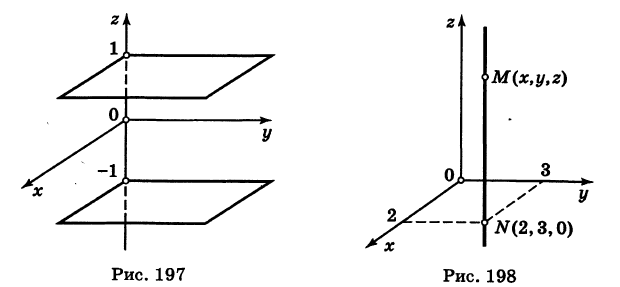
Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

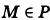
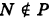
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

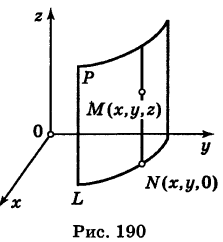
Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 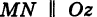(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

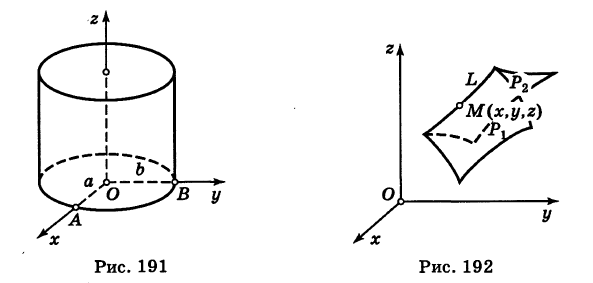
Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

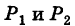
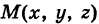
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 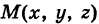, координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

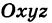
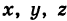
Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

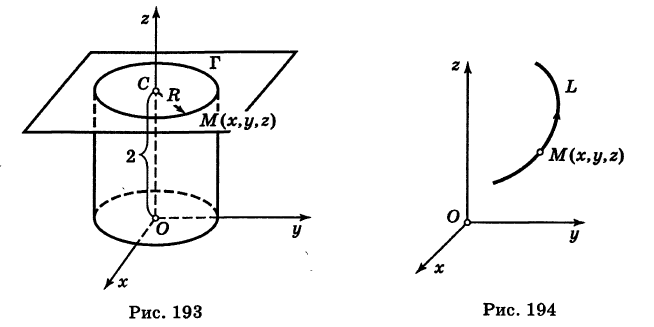
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 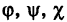— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

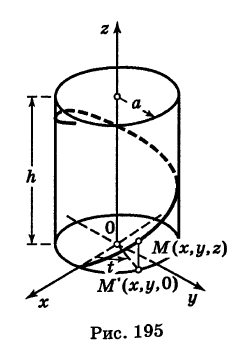
Написать уравнения винтовой линии радиуса а и шага 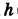(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 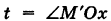и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

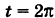
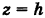
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 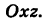. Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

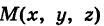
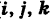
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

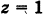
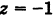
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Поверхности

Простые поверхности.

Будем говорить, что функция \(f(u, v)\) непрерывно дифференцируема на замкнутом множестве \(E \subset \boldsymbol^<2>\), если она определена и имеет непрерывные частные производные \(\partial f/\partial u\) и \(\partial f/\partial v\) на открытом множестве \(G\), содержащем замкнутое множество \(E\).

Пусть \(\Omega\) — ограниченная область в \(\boldsymbol^<2>\), а функции \(\varphi(u, v)\), \(\psi(u, v)\) и \(\chi(u, v)\) непрерывно дифференцируемы на замкнутом множестве \(\overline <\Omega>= \Omega \cup \partial \Omega\), где \(\partial \Omega\) — граница области \(\Omega\). Тогда отображение \(F: \overline <\Omega>\rightarrow \boldsymbol^<3>\), определяемое формулами
$$
x = \varphi(u, v),\quad y = \psi(u, v),\quad z = \chi(u, v),\quad (u, v) \in \overline<\Omega>,\label
$$
называется непрерывно дифференцируемым.

Если при этом в каждой точке \((u, v) \in \Omega\) ранг функциональной матрицы
$$
\begin\varphi_(u, v)&\psi_(u, v)&\chi_(u, v)\\\varphi_(u, v)&\psi_(u, v)&\chi_(u, v)\end\label
$$
равен двум, то отображение \(F: \rightarrow \boldsymbol^<3>\) называется гладким.

Если \(\overline<\Omega>\) есть замкнутое ограниченное множество в \(\boldsymbol^<2>\), a \(F: \overline <\Omega>\rightarrow \boldsymbol^<3>\) есть такое гладкое отображение, что соответствие между множествами \(\overline<\Omega>\) и \(\Sigma = F(\overline<\Omega>)\) является взаимно однозначным, то будем множество \(\Sigma\) называть простой поверхностью в \(\boldsymbol^<3>\), а уравнения \eqref будем называть параметрическими уравнениями простой поверхности \(\Sigma\).

Пусть область \(\Omega\) ограничена простым гладким или кусочно гладким контуром \(\gamma\). Образ кривой \(\gamma\) при гладком отображении \(F: \overline <\Omega>\rightarrow \boldsymbol^<3>\) будем называть краем простой поверхности \(\Sigma\) и обозначать через \(\partial \Sigma\).

Если уравнение кривой \(\gamma\) имеет вид
$$
u = u(t),\quad v = v(t),\quad \alpha \leq t \leq \beta,\nonumber
$$
то уравнение \(\partial\Sigma\) задается следующими формулами:
$$
x = \varphi(u(t), v(t)),\quad y = \psi(u(t), v(t)),\quad z = \chi(u(t), v(t)),\quad \alpha \leq t \leq \beta.\label
$$

График функции \(z = f(x, y)\), непрерывно дифференцируемой на замкнутом ограниченном множестве \(\overline <\Omega>\subset \boldsymbol^<2>\), есть простая поверхность, определяемая параметрическими уравнениями
$$
x = u,\quad y = v,\quad z = f(u, v),\quad (u, v) \in \overline<\Omega>.\label
$$

В этом случае матрица \(\beginx_&x_\\x_&y_\end\) является единичной, а поэтому ранг матрицы \eqref равен двум.

Например, график функции \(z = x^ <2>+ y^<2>\), \((x, y) \in \overline<\Omega>\), где \(\overline <\Omega>= \ <(x, y): x^<2>+ y^ <2>\leq 1\>\), есть простая поверхность. Окружность, получаемая при пересечении параболоида вращения \(z = x^ <2>+ y^<2>\) и плоскости \(z = 1\), является краем рассматриваемой простой поверхности.

Уравнения \eqref простой поверхности можно записать и в векторной форме:
$$
\boldsymbol = \boldsymbol(u, v),\quad (u, v) \in \overline<\Omega>,\quad \boldsymbol(u, v) = \varphi(u, v) \boldsymbol + \psi(u, v) \boldsymbol + \chi(u, v) \boldsymbol.\label
$$

С механической точки зрения формулы \eqref определяют гладкую (без разрывов и изломов) деформацию плоской области \(\Omega\) в множество \(\Sigma\) (простую поверхность в пространстве \(\boldsymbol^<3>\)). Для практических целей только простых поверхностей недостаточно. Например, сфера \(x^ <2>+ y^ <2>+ z^ <2>= a^<2>\) не является простой поверхностью в \(\boldsymbol^<3>\). Интуитивно ясно, что сферу нельзя получить никакой гладкой деформацией плоской области.

Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.

Пусть \(\Omega\) — плоская область и \(F: \overline <\Omega>\rightarrow \boldsymbol^<3>\) — непрерывно дифференцируемое отображение. Будем множество \(\Sigma = F(\overline<\Omega>)\) называть почти простой поверхностью в \(\boldsymbol^<3>\), если найдется расширяющаяся последовательность ограниченных областей \(\<\Omega_\>\) таких, что \(\overline<\Omega>_ \subset \Omega_\), \(\Omega = \displaystyle\bigcup_^<\infty>\Omega_\) и поверхности \(\Sigma_ = F(\overline<\Omega>_)\) простые.

Сфера \(S = \ <(x, y, z): x^<2>+ y^ <2>+ z^ <2>= a^<2>\>\) есть почти простая поверхность.

\(\vartriangle\) Введем сферические координаты. Тогда сфера \(S\) есть образ прямоугольника \(\overline <\Omega>= \displaystyle\left\<(\varphi, \psi): 0 \leq \varphi \leq 2\pi,\ -\frac<\pi> <2>\leq \psi \leq \frac<\pi><2>\right\>\) при непрерывно дифференцируемом отображении \(F: \overline <\Omega>\rightarrow S\), определяемом формулами
$$
x = a \cos \varphi \cos \psi,\qquad y = a \sin \varphi \cos \psi,\qquad z = a \sin \psi.\nonumber
$$

Образами отрезков \(\varphi = \varphi_<0>\), \(\displaystyle-\frac<\pi> <2>\leq \psi \leq \frac<\pi><2>\) являются меридианы, а при \(\displaystyle|\psi_<0>| Рис. 52.1

Конус \(K = \ <(x, y, z): x^<2>+ y^ <2>= z^<2>\>\) есть почти простая поверхность.

\(\vartriangle\) Введем цилиндрические координаты. Тогда конус \(K\) есть образ полуполосы
$$
\overline <\Omega>= \ <(r, \varphi): 0 \leq r Рис. 52.2

Легко проверить, что \(\overline<\Omega>_ \subset \Omega_\), \(\Omega = \displaystyle\bigcup_^<\infty>\Omega_\) и что поверхности \(\Sigma_ = F(\overline<\Omega>_)\) являются простыми. Поэтому конус \(K\) — почти простая поверхность. \(\blacktriangle\)

Если \(\Sigma\) есть простая поверхность, заданная векторным уравнением \eqref, а непрерывно дифференцируемые функции
$$
u = u(u’, v’),\ v = v(u’, v’),\ (u’, v’) \in \Omega’\nonumber
$$
задают взаимно однозначное отображение замыкания области \(\Omega’\) на замыкание ограниченной области \(\Omega\), причем якобиан отображения
$$
\frac<\partial(u, v)> <\partial(u’, v’)>= \begin\displaystyle\frac<\partial u><\partial u’>&\displaystyle\frac<\partial u><\partial v’>\\\displaystyle\frac<\partial v><\partial u’>&\displaystyle\frac<\partial v><\partial v’>\end\nonumber
$$
отличен от нуля в \(\overline<\Omega>’\), то уравнение
$$
\boldsymbol = \boldsymbol (u(u’, v’), v(u’, v’)) \equiv \boldsymbol<\rho>(u’, v’);\quad (u’, v’) \in \Omega’,\label
$$
определяет ту же простую поверхность, что и уравнение \eqref. Уравнения \eqref и \eqref называют различными параметризациями поверхности \(\Sigma\).

Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области \(\Omega\).

\(\vartriangle\) Переход от уравнений \eqref к уравнениям \eqref задается формулами
$$
u = a \cos \varphi \cos \psi,\quad v = a \sin \varphi \cos \psi,\quad (\varphi, \psi) \in \Omega’.\label
$$

Якобиан отображения \eqref равен \(a^ <2>\sin \varphi \cos \psi\) и обращается в нуль при \(\psi = 0\), то есть на части границы области \(\Omega’\). Это приводит к тому, что при переходе к параметризации \eqref частные производные функции \(z = \sqrt-u^<2>-v^<2>>\) стремятся к бесконечности при приближении точки \(u, v\) к окружности \(u^ <2>+ v^ <2>= a^<2>\). \(\blacktriangle\)

Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.

Криволинейные координаты на поверхности.

Пусть простая поверхность \(\Sigma\) задана векторным уравнением \eqref. Предположим, что область \(\Omega\) выпукла, \([a, b]\) есть проекция области \(\Omega\) на ось \(u\). Если \(u_ <0>= \in (a, b)\), то прямая \(u = u_<0>\) будет пересекаться с областью \(\Omega\) по отрезку \(u = u_<0>\), \(\alpha \leq v \leq \beta\) (рис. 52.3). Образ этого отрезка при отображении \eqref есть кривая
$$
\boldsymbol = \boldsymbol (u_<0>, v),\ \alpha \leq v \leq \beta,\label
$$
лежащая на поверхности \(\Sigma\). Будем называть ее координатной кривой \(u = u_<0>\). Придавая \(u_<0>\) все значения из отрезка \([a, b]\), получим семейство координатных кривых \(u = \operatorname\). Аналогично строится и семейство координатных кривых \(v = \operatorname\).

Рис. 52.3

В силу взаимной однозначности отображения \eqref каждая точка \(A\) поверхности \(S\) однозначно определяется как пересечение двух координатных кривых, \(u = u_<0>\) и \(v = v_<0>\). Пара чисел \((u_<0>, v_<0>)\) называется криволинейными координатами точки \(A\) поверхности. Запись \(A(u_<0>, v_<0>)\) означает, что точка \(A\) поверхности \(\Sigma\) задана криволинейными координатами \((u_<0>, v_<0>)\).

Например, в сферических координатах часть сферы \(x^ <2>+ y^ <2>+ z^ <2>= a^<2>\), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах \(\varphi\), \(\psi\) следующим образом:
$$
\varphi_ <1>\leq \varphi \leq \varphi_<2>,\quad \psi_ <1>\leq \psi \leq \psi_<2>.\nonumber
$$

На сфере координатные кривые \(\varphi = \operatorname\) — меридианы, а координатные кривые \(\psi = \operatorname\) — параллели.

На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.

Вектор-функция \(\boldsymbol (u_<0>, v)\) есть непрерывно дифференцируемая функция параметра \(v\), и, следовательно, координатная кривая \(u = u_<0>\), определяемая равенством \eqref, является непрерывно дифференцируемой. Вектор \(\boldsymbol_ (u_<0>, v_<0>)\) является касательным к этой кривой в точке \(A(u_<0>, v_<0>)\). Аналогично, вектор \(\boldsymbol_ (u_<0>, v_<0>)\) касателен к координатной кривой \(v = v_<0>\) в точке \(A(u_<0>, v_<0>)\). Заметим, что векторы \(\boldsymbol_ (u_<0>, v_<0>)\) и \(\boldsymbol_ (u_<0>, v_<0>)\) не могут обратиться в нуль, так как в этом случае ранг матрицы \eqref будет меньше двух. Следовательно, для простой поверхности координатные кривые являются гладкими.

Если область \(\Omega\) не является выпуклой, а точка \((u_<0>, v_<0>)\) лежит внутри \(\Omega\), то нужно взять выпуклую окрестность точки \((u_<0>, v_<0>)\), лежащую внутри \(\Omega\). Тогда образ этой выпуклой окрестности будет куском поверхности \(\Sigma\) и координатные кривые можно строить на этом куске поверхности (локально).

Касательная плоскость и нормаль к поверхности.

Пусть \(\Sigma\) есть простая поверхность, заданная уравнениями \eqref или векторным уравнением \eqref. Рассмотрим точку \(A(u, v)\) на поверхности \(\Sigma\), где \((u, v)\) — внутренняя точка области \(\Omega\). Построим координатные линии \(u = \operatorname\) и \(v = \operatorname\), проходящие через точку \(A(u, v)\). Векторы \(\boldsymbol_ (u, v)\) и \(\boldsymbol_ (u, v)\) будут касательными к соответствующим координатным линиям.

В любой точке \(A(u, v)\) простой поверхности \(\Sigma\) векторы \(\boldsymbol_ (u, v)\) и \(\boldsymbol_(u, v)\) неколлинеарны. Направление вектора \(N = [\boldsymbol_, \boldsymbol_]\) при изменении способа параметризации или не меняется, или изменяется на противоположное.

\(\circ\) Рассмотрим вектор \(N = [\boldsymbol_, \boldsymbol_]\) во всех точках поверхности \(\Sigma\). Тогда
$$
\boldsymbol=\beginy_&z_\\y_&z_\end\boldsymbol + \beginz_&x_\\z_&x_\end\boldsymbol + \beginx_&y_\\x_&y_\end\boldsymbol.\nonumber
$$
Если \(\boldsymbol = \boldsymbol<0>\), то все компоненты вектора \(\boldsymbol\) равны нулю, и ранг матрицы \eqref будет меньше двух, что невозможно для простой поверхности. Пусть поверхность \(\Sigma\) параметризована двумя способами, \eqref и \eqref. Тогда, воспользовавшись правилом нахождения частных производных сложной функции и аддитивностью и кососимметричностью векторного произведения, получаем
$$
\boldsymbol’ = [\boldsymbol<\rho>_, \boldsymbol<\rho>_] = [\boldsymbol_ \frac<\partial u> <\partial u’>+ \boldsymbol_ \frac<\partial v><\partial u’>,\ \boldsymbol_ \frac<\partial u> <\partial v’>+ \boldsymbol_ \frac<\partial v><\partial v’>] =\\= [\boldsymbol_, \boldsymbol_] \left(\frac<\partial u><\partial u’>\frac<\partial v><\partial u’>-\frac<\partial u><\partial v’>\frac<\partial v><\partial v’>\right) = [\boldsymbol_, \boldsymbol_] \frac<\partial(u, v)><\partial(u’, v’)>,\nonumber
$$
то есть
$$
\boldsymbol’ = \boldsymbol \frac<\partial(u, v)><\partial(u’, v’)>.\label
$$
Так как якобиан \(J = \displaystyle\frac<\partial(u, v)><\partial(u’, v’)>\) не обращается в нуль в области \(\Omega’\), то векторы \(\boldsymbol’\) и \(\boldsymbol\) коллинеарны. Эти векторы сонаправлены, если \(J > 0\), и противоположно направлены, если \(J Лемма 2.

Вектор нормали к простой поверхности \(\Sigma\) в точке \(A(u_<0>, v_<0>)\) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку \(A(u_<0>, v_<0>)\).

\(\circ\) В самом деле, такая кривая есть образ при отображении \eqref некоторой гладкой кривой, лежащей в области \(\Omega\) и задаваемой уравнениями \(u = u(t)\), \(v = v(t)\), \(\alpha \leq t \leq \beta\).

Уравнение кривой на поверхности тогда имеет вид
$$
\boldsymbol = \boldsymbol(u(t), v(t)),\ \alpha \leq t \leq \beta,\ u(t_<0>) = u_<0>,\ v(t_<0>) = v_<0>.
$$

Касательный вектор \(\boldsymbol<\tau>\) к этой кривой в точке \(A\) есть
$$
\boldsymbol <\tau>= \frac