Простейшие тригонометрические уравнения и неравенства конспект

Простейшие тригонометрические уравнения. Простейшие тригонометрические неравенства
план-конспект занятия

1) образовательная: организовать деятельность студентов по изучению и первичному закреплению простейших тригонометрических уравнений и неравенств;

2) воспитательная: воспитывать самостоятельность, информационную компетентность;

3) развивающая: развивать внимание, память, познавательный интерес к учебной дисциплине.

Скачать:

Предварительный просмотр:

Технологическая карта практического занятия

Название УД, ПМ, раздела, МДК: Математика

Специальность, группа: 09.02.07 Информационные системы и программирование, 14 группа

Тема занятия: Простейшие тригонометрические уравнения. Простейшие тригонометрические неравенства

1) образовательная: организовать деятельность студентов по изучению и первичному закреплению простейших тригонометрических уравнений и неравенств;

2) воспитательная: воспитывать самостоятельность, информационную компетентность;

3) развивающая: развивать внимание, память, познавательный интерес к учебной дисциплине.

• обеспечение сформированности представлений о социальных, культурных и исторических факторах становления математики;

• обеспечение сформированности логического, алгоритмического и математического мышления;

• обеспечение сформированности умений применять полученные знания при решении различных задач;

сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

Умение организовать собственную деятельность, определение методов и способов выполнения профессиональных задач, оценивание их эффективности и качества.

Уровень освоения: 1,2.

Междисциплинарные связи: истоки, выход

Материально-техническое оснащение: ПК, презентация, проектор, интерактивна доска.

Учебно-методическое оснащение: рабочая программа, презентация, КТП, технологическая карта урока, практическая работа.

План -конспект урока алгебры в 10 классе Тема урока: Простейшие тригонометрические уравнения и их решения

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

ГУ « Средняя общеобразовательная школа 5» отдела образования акимата г. Костаная

ФИО (полностью) Пластун Сергей Владимирович

Предмет Алгебра и начала анализа

Базовый учебник ОҚУЛЫҚ: АЛГЕБРА и НАЧАЛА АНАЛИЗА, АЛМАТЫ «МЕКТЕП», 2016

Авторлары: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

УЧЕБНИК: АЛГЕБРА И НАЧАЛА АНАЛИЗА, АЛМАТЫ «МЕКТЕП», 2016

Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

Дополнительная литература ОҚУЛЫҚ: АЛГЕБРА И НАЧАЛА АНАЛИЗА, ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ, АЛМАТЫ «МЕКТЕП», 2016

УЧЕБНИК: АЛГЕБРА, ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ, АЛМАТЫ «МЕКТЕП», 2013

Тема урока: Простейшие тригонометрические уравнения и их решения

Образовательная

ввести понятия – тригонометрическое уравнение, простейшее тригонометрическое уравнение;

ввести формулы корней простейших тригонометрических уравнений;

сформировать умение решать простейшие тригонометрические уравнения на репродуктивном уровне.

Развивающая

развивать и совершенствовать умения применять имеющиеся знания в измененной ситуации;

развивать умение делать выводы, анализировать;

развивать и совершенствовать навыки самоконтроля.

Воспитательная

выработка привычки к постоянной занятости каким-либо полезным делом;

Форма: частично- поисковый

Оборудование: дидактические материалы

на листочках напечатаны основные тригонометрические формулы дидактические материалы

Тип урока: изучение новой темы (по основной дидактической цели): комбинированный

Метод: частично поисковый

Этап проверки домашнего задания.

Ознакомление с темой урока. Постановка целей и задач.

Этап усвоения новых знаний и способов действий.

Этап первичной проверки понимания изученного.

Этап закрепления и всесторонней проверки знаний (контроля и самоконтроля знаний и способов действий).

Этап информации о домашнем задании.

Этап подведения итогов. Рефлексия.

свойства тригонометрических функций;

арксинус, арккосинус, арктангенс и арккотангенс;

Межпредметная связь – информатика (алгоритм, свойства алгоритма

СТРУКТУРА И ХОД УРОКА

иллюстрация, демонстрация и т. д.)

Мотивационное начало урока.

Вводная беседа с использованием презентации

Проверка домашнего задания

Повторение пройденного материала

Индивидуальная работа по карточкам

Подведение итогов, постановка домашнего задания

Организационный момент . Взаимное приветствие учителя и учащихся. Определение отсутствующих, проверка подготовленности учащихся к уроку, организация внимания учащихся

Проверка домашнего задания : Выявления уровня знаний учащимися заданного на дом материала; определение типичных недостатков в знаниях и причин их появления; ликвидация обнаруженных недочетов.

Всесторонняя проверка знаний : Стимулировать опрашиваемых и весь класс к овладения рациональными приемами умения и самообразования

Постановка цели: Подготовка учащихся к активному и сознательному усвоению знаний. Сообщение темы, цели и задачи изученного материала. Постановка перед учащимися цели урока.

Задача: подготовить учащихся к работе на уроке.

установить наличие, правильность и осознанность выполнения д/з всеми учащимися;

выявить пробелы в знаниях и способах деятельности учащихся, которые будут устранены в ходе урока.

1) Проверка д/з по кодоскопу (наличие и правильность).

Учитель выясняет, что учащиеся не поняли, при выполнении каких заданий были совершены ошибки. Ученики проверяют д/з, делают исправления.

2) Всему классу предлагается устный диктант.

Назовите область определения для функции y = sin x , y = cos x , y = tg x .

Что называется arcsin a ? В каких пределах лежит число а?

Что называется arccos a ? В каких пределах лежит число а?

При каких значениях х имеют смысл выражения: а) arcsin 4 x ; в) arccos (3 x – 2).

В промежутке [0;  ] найдите значения аргумента х, если: а) cos x =; в) ctg х = .

Учитель следит за правильностью ответов учащихся.

3) Самостоятельная работа (задания подобны д/з, проверка осознанности выполнения д/з).

КСР (контролирующая самостоятельная работа).

Вычислите, пользуясь таблицей и свойствами:

а) ; б) ; в) ; г) ; д) .

Найдите значения выражений: а) ; б) .

3) Найдите количество корней уравнения на отрезке [ —  ; 0].

Решите уравнение: . Указание: воспользуйся определением арккосинуса числа.

Учитель следит за выполнением с/р. По истечении времени предлагает учащимся осуществить взаимопроверку работы по «ключу». Учащиеся проверяют работу друг друга, записывают Ф.И. проверяющего.

III . Ознакомление с темой урока. Постановка целей и задач.

Задача: обеспечить мотивацию учения школьников; постановка целей через показ конечных результатов.

Вводная беседа учителя. Записывается тема урока. Учитель задает учащимся вопросы:

что называется уравнением;

что означает «решить уравнение».

Учитель дает определение тригонометрических уравнений. Обращает внимание учащихся на плакат, предлагает проанализировать представленные уравнения и назвать те из них, которые не являются тригонометрическими (понимание нового термина):

1) 2sin x + = 0; 2) cos 4x = 0; 3) cos ; 4) 2sin x + 2 = 0;

5) 2cos x + 5 = 0; 6) cos  + х = 0; 7) с tg x +1 = 0; 8) 3tg x — = 0.

Ученики анализируют, поднимают руки, объясняют свой выбор.

Учитель внимательно слушает, поправляет, поощряет. Обращает внимание учащихся на плакат-схему «Тригонометрические уравнения», проводит классификацию тригонометрических уравнений (простейшие, решаемые с помощью формул тригонометрии, приводимые к квадратным, однородные и приводимые к ним). Обращает внимание на то, что на этом уроке будет идти речь только о простейших тригонометрических уравнениях, к которым сводятся все остальные виды.

Выделяет, что должны знать и уметь учащиеся. Оформляется блок «Опорные знания и умения».

Задача: обеспечить восприятие, осмысление и первичное запоминание учащимися изучаемого материала:

существенных признаков, понятий;

правил и построенных на их основе алгоритмов.

Учитель вводит понятие «простейшее тригонометрическое уравнение». При объяснении новой темы используется плакат «Уравнение y = sin x , y = cos x » (Таблицы по алгебре и началам анализа. 10 класс). Предлагает совместными усилиями построить блок-схему решения простейшего тригонометрического уравнения вида cos t = a . Рассматриваются частные случаи решения.

Задаются вопросы (межпредметная связь):

что называется алгоритмом;

Оформляется блок-схема (см. блок-схему).

После оформления блок-схемы учащимся предлагается задание – самостоятельно заполнить блок-схему решения уравнения вида sin t = a , используя текст параграфа (заполняют карандашом, время — 5 мин). По истечении времени на доску проецируется слайд с верным ответом. Учащиеся проверяют, делают исправления. Затем объясняется решение уравнений вида tg t = a , ctg t = a .

V . Этап первичной проверки понимания изученного.

Задача: установить усвоены ли понятия «простейшее тригонометрическое уравнение», «частные случаи решения».

(работа по формированию знаний)

Учитель предлагает, используя плакат, указать:

простейшие тригонометрические уравнения, заданные в явном виде;

среди этих уравнений указать те, которые не имеют решений; имеют частные случаи решения;

как привести уравнение 4) к простейшему виду.

1) sin x = ; 2) cos 4x = 0; 3) cos ; 4) sin 2x + = 0; 5) 2cos x = 5.

Ученики размышляют, анализируют, отвечают. Учитель подробно, используя блок-схему объясняет решение уравнений 1), 3). Затем вызванные по желанию учащиеся решают уравнения 4), 2) – комментированное решение.

VI . Этап закрепления и всесторонней проверки знаний и способов действий.

выявить уровень усвоения новых знаний и способов действий;

обеспечить развитие у школьников способности к оценочным действиям.

У доски решаются параллельно уравнения № 140 (а – с комментарием, б – объяснение решения дается после выполнения задания).

Учащимся предлагается выполнить СФН (самостоятельную работу по формированию навыков), дается инструктаж по ее выполнению

1) sin x = — 2; 2) cos x = 1; 3) cos x = —.

1) sin 2x =0; 2) 2sin – 1 = 0.

1) sin 2 x — 4sin x = 0; 2) cos 2 x + cos x = 0.

1) cos х = 2; 2) sin x = — 1; 3) sin x =.

1) cos 4x = — 1; 2) 2cos – 1 = 0.

1) cos 2 x + 3cos x = 0; 2) sin 2 x — sin x = 0.

Учитель по истечении времени предлагает учащимся цветной пастой проверить правильность выполнения самостоятельной работы (по «ключу»). Учащиеся проверяют свои работы, зачеркивают неверные ответы. Тетради собираются на проверку для последующего анализа.

Анализ выполнения такой работы помогает учителю:

выявить «слабые места» каждого ученика, и класса в целом;

скорректировать и организовать дальнейшее изучений темы с учетом «слабых мест»;

целенаправленно применять самостоятельные коррекционные работы или карточки.

VII . Этап информации о домашнем задании.

Задача: сообщить учащимся домашнее задание, дать инструктаж по его выполнению.

VIII . Этап подведения итогов. Рефлексия.

Задача: дать качественную оценку работы класса и отдельных учащихся. Цветограмма урока.

«В любом деле победа начинается с первого шага»

Перед уроком учитель выдает ученикам карточки трех цветов:

Карточка красного цвета обозначает: «Я удовлетворен уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, я получил заслуженную оценку, я понимал все, о чем говорилось и что делалось на уроке».

Карточка желтого цвета обозначает: «Урок был интересен, и я принимал в нем активное участие, урок был в определенной степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно».

Карточка зеленого цвета обозначает: «Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я был не готов».

В конце урока каждый ученик сдает учителю карточку того цвета, который соответствует его оценке урока (фамилия на карточках не указывается). Такой прием позволяет получить цветовой индекс дня в школе в целом, по каждому учителю отдельно и на каждый час.

Примечание. Эти цветные карточки можно прикрепить к доске, получится наглядная цветограмма урока.

Простейшие тригонометрические уравнения (задание 5) и неравенства

\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b\) , которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb\) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).

Рассмотрим несколько примеров:

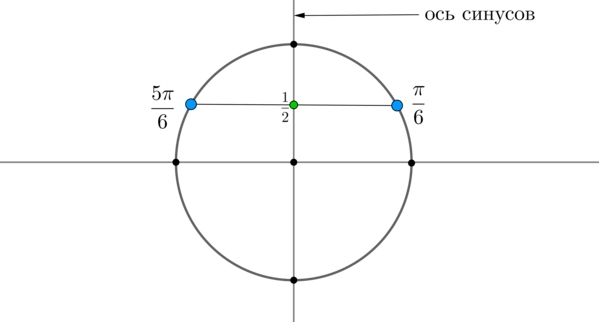
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .

Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb\) .

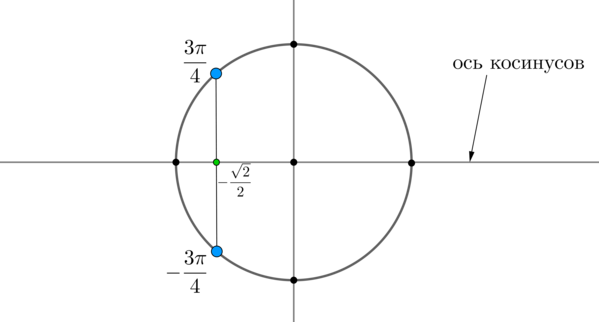
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .

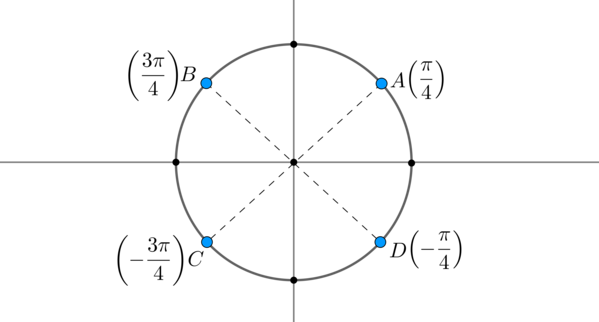
Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb\) .

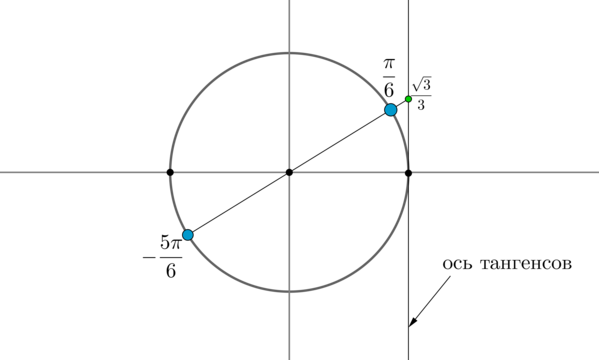
Пример 3. Решить уравнение \(\mathrm\,x=\dfrac<\sqrt3>3\) .

Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

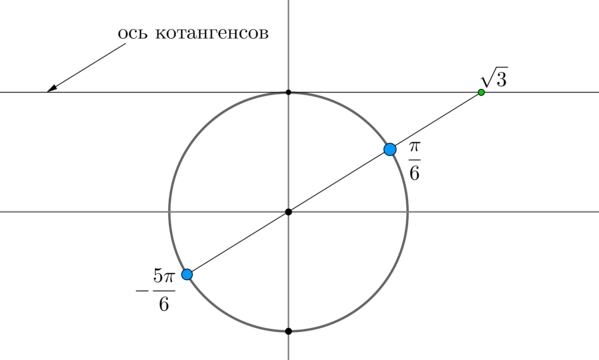
Пример 4. Решить уравнение \(\mathrm\,x=\sqrt3\) .

Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .

\(\blacktriangleright\) Любые уравнения вида \(\mathrm\,\big(f(x)\big)=a\) , (где \(\mathrm\) — одна из функций \(\sin, \ \cos, \ \mathrm,\ \mathrm\) , а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\) .

Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .

Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb\) .

Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb\) , где \(\alpha\) — один из этих углов.

Рассмотрим данную ситуацию на примере:

Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb\) . Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over\) равны \(\dfrac<\pi>2\) , то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb\) .

где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .

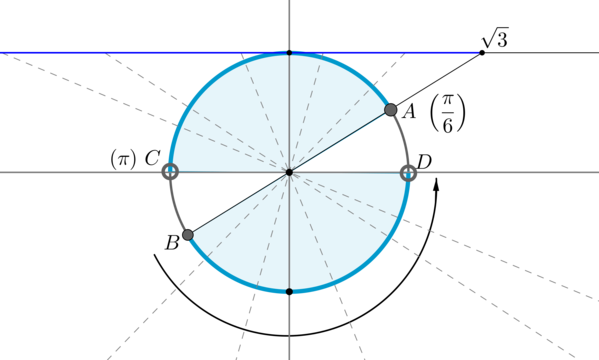
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .

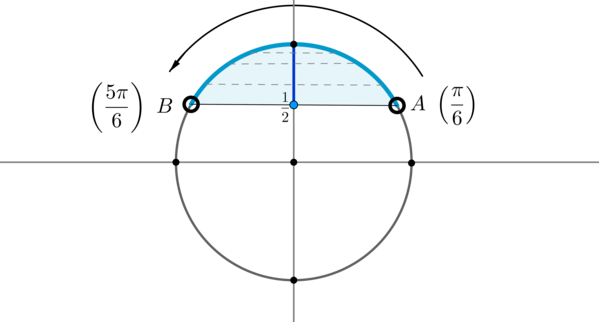
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb\) , т.к. у синуса период \(2\pi\) .

Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

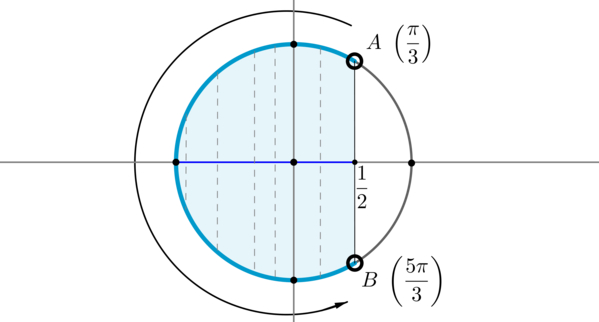
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb\) , т.к. у косинуса период \(2\pi\) .

Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm\, x \geq \dfrac<\sqrt<3>>3\) .

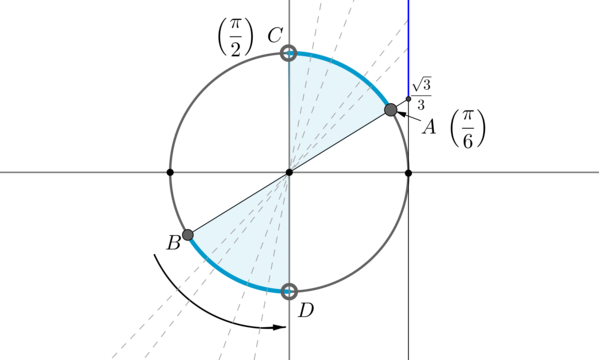
Для начала отметим на окружности корни уравнения \(\mathrm\, x = \dfrac<\sqrt<3>>3\) . Это точки \(A\) и \(B\) . Все точки, тангенс которых больше или равен \(\dfrac<\sqrt<3>>3\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac<\pi>2\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\dfrac<\pi>2\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb\) , т.к. у тангенса период \(\pi\) .

Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm\, x \leq \sqrt<3>\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \sqrt<3>\) . Это точки \(A\) и \(B\) . Все точки, котангенс которых меньше или равен \(\sqrt<3>\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\pi\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\pi\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb\) , т.к. период котангенса \(\pi\) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

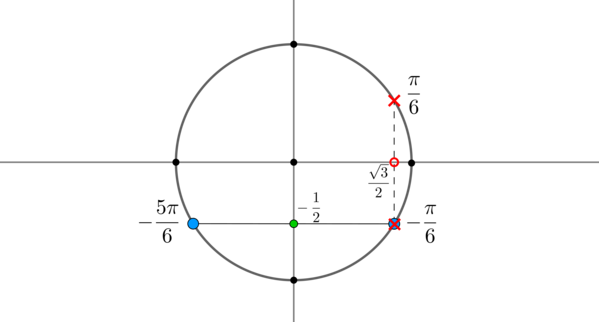
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb\) , решением второго являются \(x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb\) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb\) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему \(\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end\)

Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) . Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:

\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.

Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) .

Алгебраический способ.

Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .

Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb\) . Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq x_2\leq\pi\) :

\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .

Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .

Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.

Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :

Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .

Ответ: \((-5p-1; 3p+1), p\in\mathbb\) .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.

Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac2\) .

Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac2=\frac<2p+1>2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\) , то \(\frac2=\frac<2p+1+1>2=p+1= \) целому числу.

Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb\) .

Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb\) .