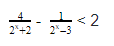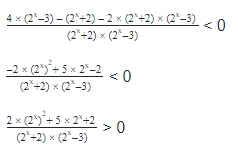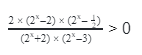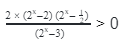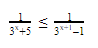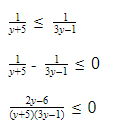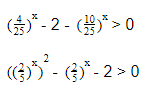Простейшие уравнения и неравенства 10 класс

Простейшие тригонометрические уравнения. Урок алгебры в 10-м классе

Презентация к уроку

Загрузить презентацию (608 кБ)

Тип урока: урок формирования новых знаний.

Форма урока: урок с применением информационно-коммуникационных технологий (работа с интерактивной доской).

— сформировать знания по новой теме в соответствии с программными требованиями;

— научить применять на практике основные формулы решения тригонометрических уравнений (общие и частные);

— научить применять основные методы решения простейших тригонометрических уравнений: введения новой переменной, разложение на множители при решении задач.

— развивать навыки работы с ИК-ресурсами;

— развивать навыки самоконтроля, математическую речь.

— формировать коммуникативную, информационную компетентности, компетентность по решению проблем.

Оборудование:

I. Организационный момент.

Цель: активизация внимания и мотивации учащихся к работе на уроке:

— настрой учащихся на работу, организация внимания;

— сообщение темы и цели урока;

— проверка домашнего задания.

Проверка домашнего задания проводится выборочно. На экран демонстрируется файл учащегося, который осуществляет голосовую защиту своего решения домашнего индивидуального задания (задания повышенной сложности).

II. Актуализация знаний учащихся. Фронтальный опрос.

Цель: установить уровень знаний и осознанность их применения в рамках изученного теоретического материала, повторение пройденного материала.

Для учащихся на интерактивной доске демонстрируются задания.

1. Вычисли устно:

2. Найди ошибку при решении неравенства:

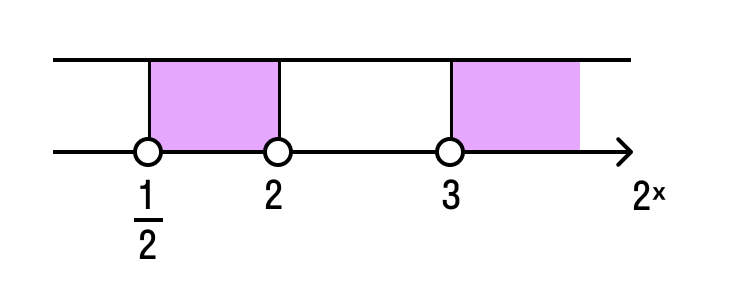
3. Какой рисунок соответствует решению соответствующего уравнения?

III. Объяснение нового материала.

Цель: формировать знания по новой теме в соответствии с программными требованиями и первичные навыки решения простейших тригонометрических уравнений; развивать математическую речь.

В ходе беседы учитель дает определение: тригонометрического уравнения, дает понятие простейшего уравнения. Проводит параллель между решением простейшего уравнения с использованием тригонометрического круга и нахождением корней тригонометрического уравнения с использованием общих формул. Затем учитель вместе с учащимися рассматривает частные случаи для решения тригонометрических уравнений (а=1, а=1, а=0). Все решения заносятся в таблицу. Объяснение нового материала сопровождается презентацией Microsoft Office Power Point. Данные таблицы представлены так же на интерактивной доске.

a=1	a=0	a= -1	,

Учитель делает акцент, что для значений лучше всего использовать частные формулы для корней тригонометрических уравнений и обращает внимание, что на столах у учащихся лежат памятки для решения тригонометрических уравнений. (Демонстрируется на слайде)

Далее учителем рассматриваются основные методы решения простейших тригонометрических уравнений и разбираются на примерах.

а) ; б) в) .

а) ,

Ответ :

б) ,

Если, то , ,

Если, то , ,

Ответ:,

в)

,

,

Ответ:, .

IV. Первичное закрепление нового материала.

Цели:

Учащимся предлагается выполнить проверочную работу обучающего характера на установление уровня усвоения нового материала. На партах лежат листы с заданиями базового и профильного уровня (уровень Б и П). Учащийся сам определяет, на каком уровне будет выполнять самостоятельную работу обучающего характера. Время на самостоятельную работу 5-6 минут.

В ответе запишите букву (код ответа) соответствующую ответу вашего решения.

По окончании самостоятельной работы учащимся предлагается выполнить самопроверку. На доске (слайд) приводятся правильные ответы.

Подводя итоги урока, учитель сопоставляет поставленные цели с результатами урока, оценивает деятельность учащихся и комментирует домашнее задание.

На экране выведено домашнее задание.

Задание на дом: §22. №№ 22.4(а), 22.5, 22.11-12(в, г),22.23(а, б), 22.25(а, б). Алгебра и начала анализа. 10 класс в 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2010 год

Дополнительное задание: (см. так же электронную почту)

Построить график функции .

Решить уравнение .

Простейшие тригонометрические уравнения (задание 5) и неравенства

\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b\) , которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb\) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).

Рассмотрим несколько примеров:

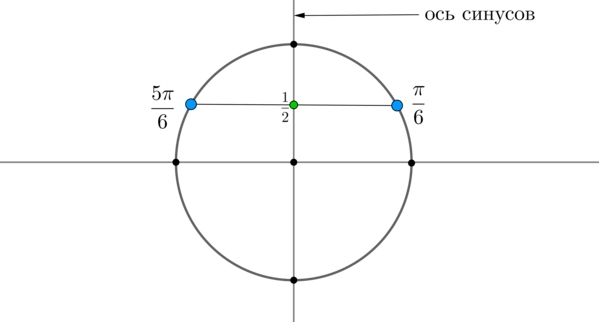
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .

Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb\) .

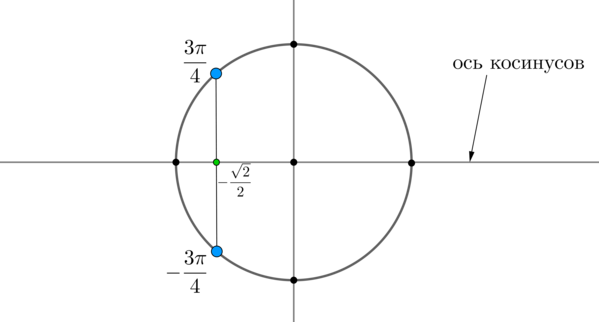
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .

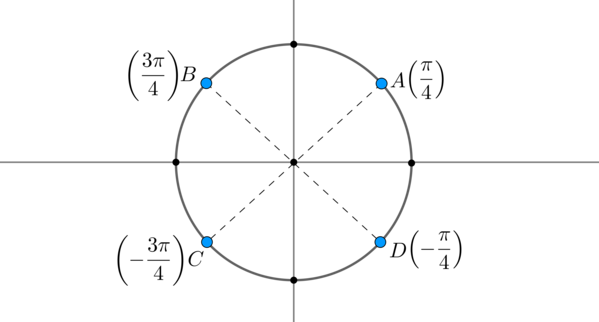
Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb\) .

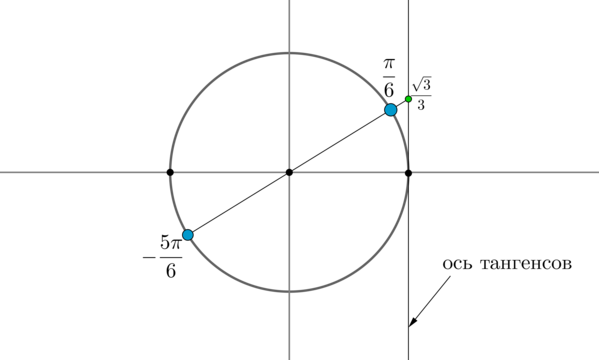
Пример 3. Решить уравнение \(\mathrm\,x=\dfrac<\sqrt3>3\) .

Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

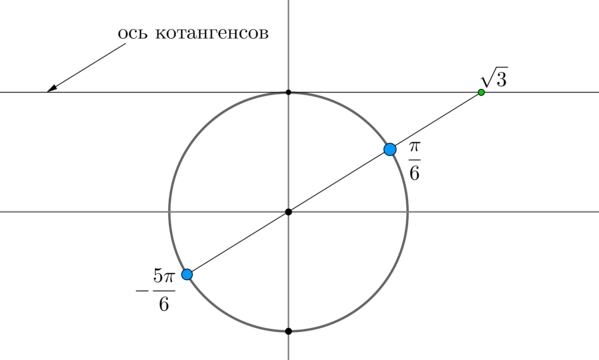
Пример 4. Решить уравнение \(\mathrm\,x=\sqrt3\) .

Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .

\(\blacktriangleright\) Любые уравнения вида \(\mathrm\,\big(f(x)\big)=a\) , (где \(\mathrm\) — одна из функций \(\sin, \ \cos, \ \mathrm,\ \mathrm\) , а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\) .

Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .

Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb\) .

Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb\) , где \(\alpha\) — один из этих углов.

Рассмотрим данную ситуацию на примере:

Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb\) . Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over\) равны \(\dfrac<\pi>2\) , то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb\) .

где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .

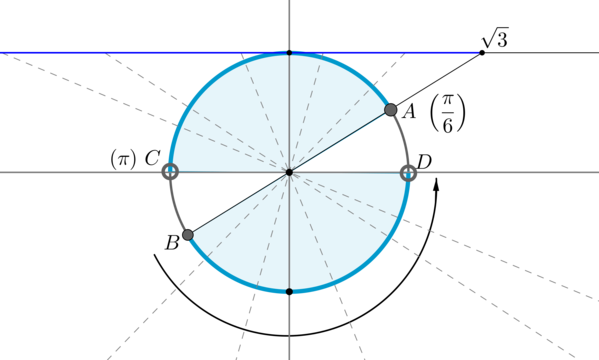
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .

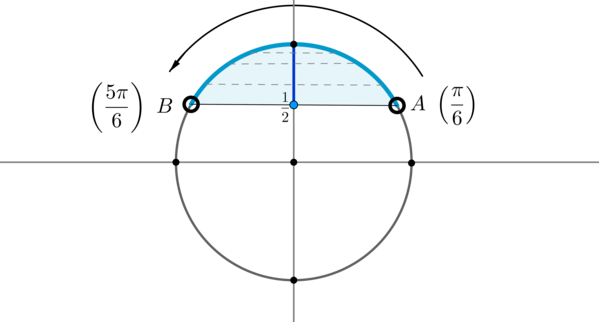
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb\) , т.к. у синуса период \(2\pi\) .

Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

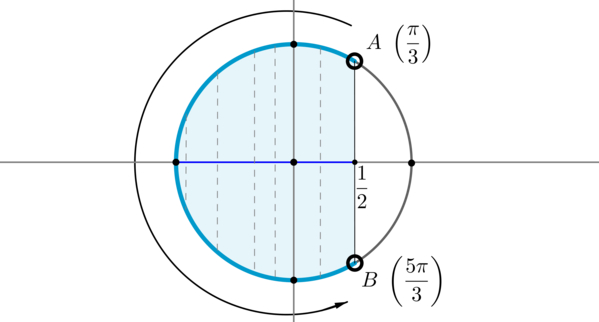
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb\) , т.к. у косинуса период \(2\pi\) .

Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm\, x \geq \dfrac<\sqrt<3>>3\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \dfrac<\sqrt<3>>3\) . Это точки \(A\) и \(B\) . Все точки, тангенс которых больше или равен \(\dfrac<\sqrt<3>>3\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac<\pi>2\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\dfrac<\pi>2\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb\) , т.к. у тангенса период \(\pi\) .

Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm\, x \leq \sqrt<3>\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \sqrt<3>\) . Это точки \(A\) и \(B\) . Все точки, котангенс которых меньше или равен \(\sqrt<3>\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\pi\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\pi\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb\) , т.к. период котангенса \(\pi\) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

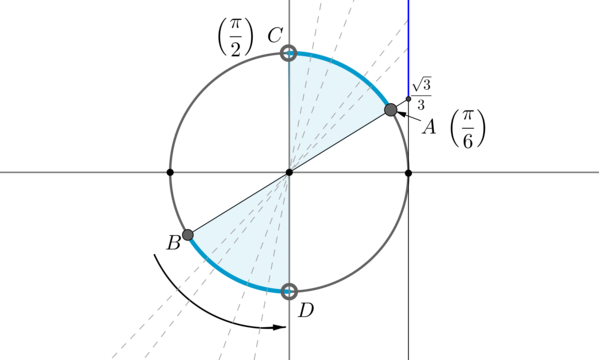
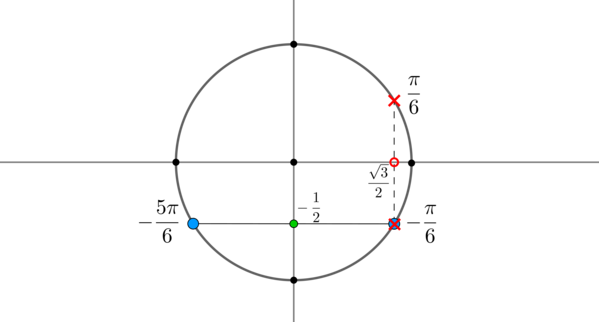
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb\) , решением второго являются \(x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb\) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb\) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему \(\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end\)

Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) . Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:

\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.

Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) .

Алгебраический способ.

Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .

Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb\) . Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq x_2\leq\pi\) :

\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .

Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .

Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.

Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :

Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .

Ответ: \((-5p-1; 3p+1), p\in\mathbb\) .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.

Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac2\) .

Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac2=\frac<2p+1>2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\) , то \(\frac2=\frac<2p+1+1>2=p+1= \) целому числу.

Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb\) .

Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb\) .

Показательные неравенства

О чем эта статья:

10 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательных неравенств

Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .

Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.

Для изучения этой темы стоит повторить:

И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.

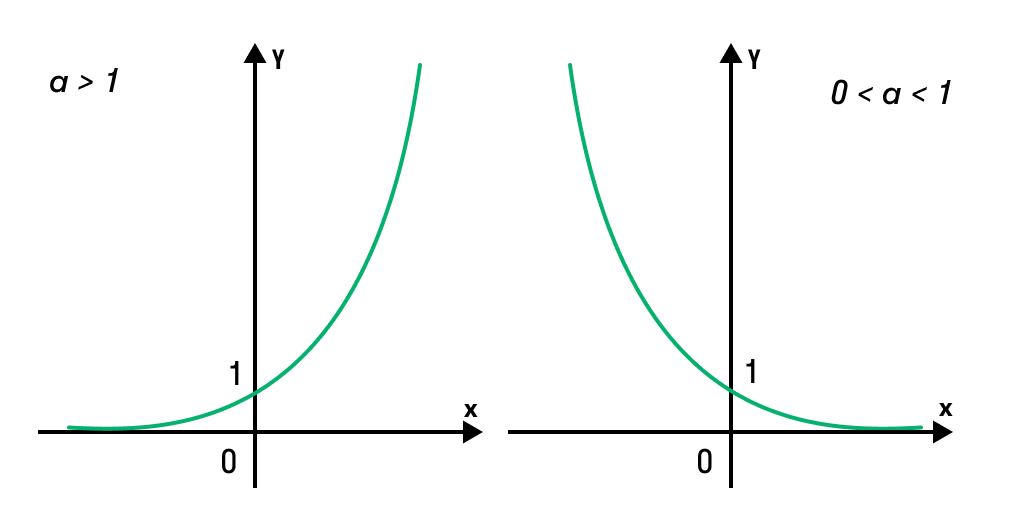
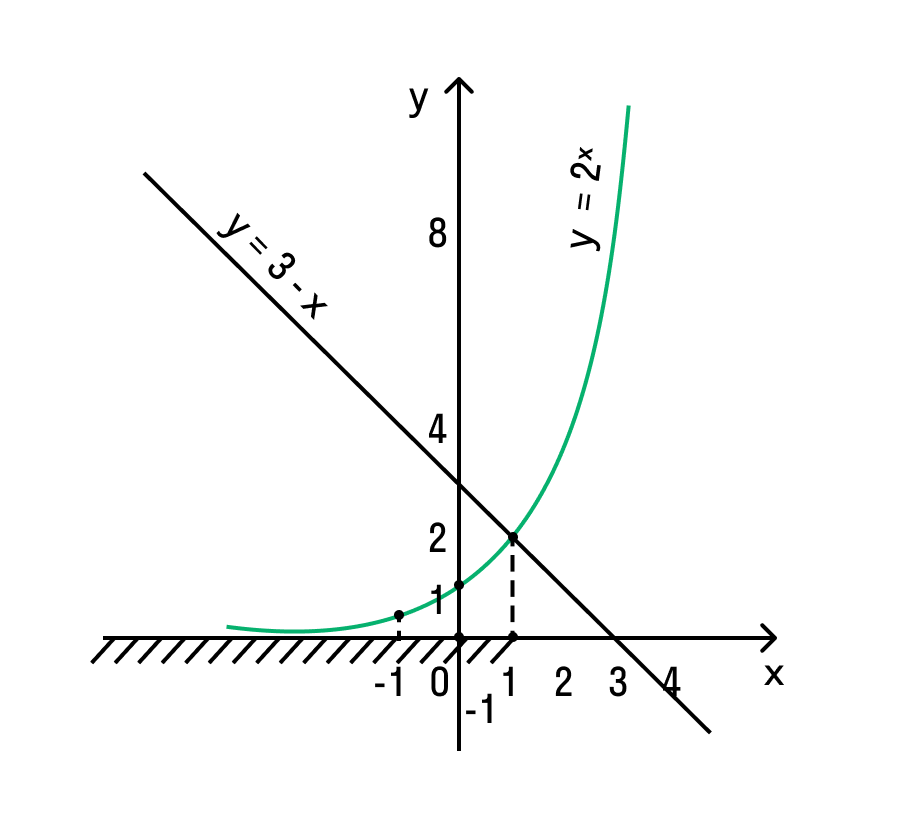
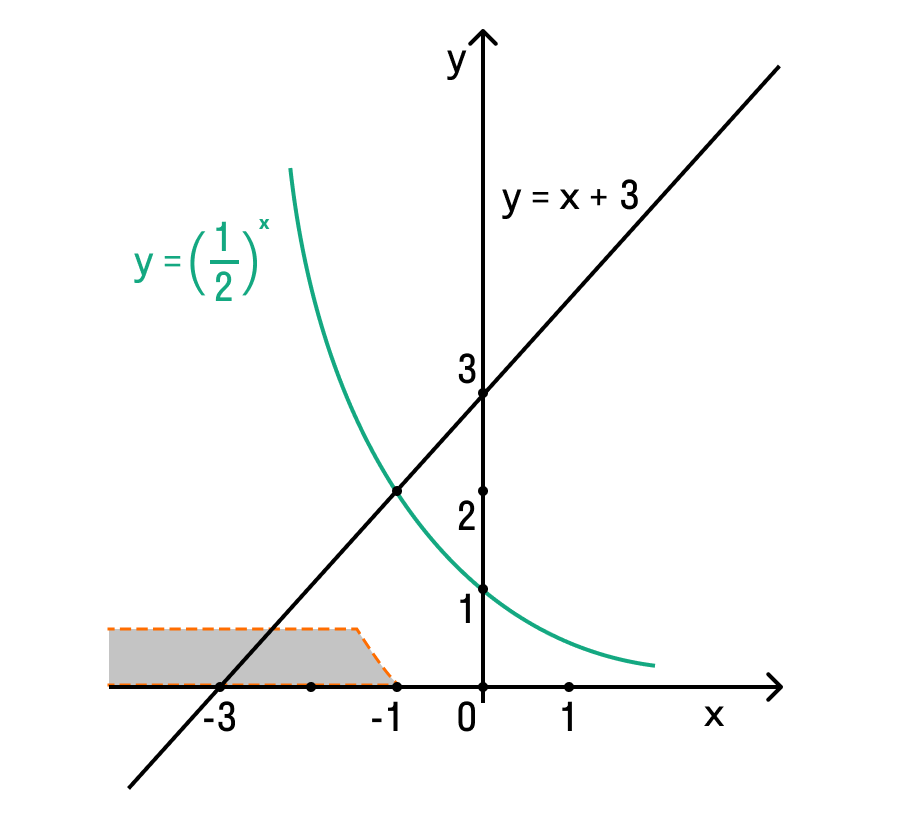
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.

При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.

Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.

Запишем следствие монотонности показательной функции в виде формул:

• a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
• a f(x) > a g(x) f(x)

Как решать показательные неравенства

Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.

Допустим, у нас есть простейшее показательное неравенство:

Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:

Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:

Проверим, верно ли в таком случае х > 2.

0,5 3 = 0, 125 и т. д.

Как видите, на самом деле в этом случае х

Если а > 1, то a x > a n a > n, и при решении неравенства можно просто убрать одинаковые основания степени.

Если 0 x > a n a

Наконец, если рассмотреть случай, когда а х > 9

Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:

Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.

Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Показательные неравенства, сводящиеся к простейшим

Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎

Попробуем на примере несложного показательного неравенства с разными основаниями.

Пример 1

Поскольку 3 больше 1, знак не меняем:

Показательные неравенства, сводящиеся к квадратным

Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.

Пример 1

Наименьший общий множитель в данном случае будет 3 х , обозначим его новой переменной у и перенесем все слагаемые в левую сторону.

(3 х ) 2 — 12 × 3 х + 27 х = у

y 2 — 12y + 27 х 1 х 2

Поскольку 3 > 1, мы не меняем знак.

1 2 x — 5 sinx + 2 2 — 5y + 2

Показательные неравенства, сводящиеся к рациональным

Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).

Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.

Пример 1

Преобразуем неравенство указанным выше способом:

(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).

Поскольку выражение 2 х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.

(2 х — 2) × (2 х — 1/2) × (2 х — 3) > 0

Пример 2

Обозначим 3 х через новую переменную y:

3 х = y, при условии что 3 х > 0.

Применим метод интервалов и получим:

Вернем на место нашу старую переменную:

Однородные показательные неравенства

Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова.

Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.

Пример 1

4 х — 2 × 5 2х — 2 х × 5 х > 0

2 × 2 х — 2 × 5 2х — 2 х × 5 х > 0

В левой части неравенства мы видим однородные функции относительно 2 х и 5 х . Следовательно, можно разделить обе части на 2 2х или 5 2х . Выберем 5 2х , т. е. 25 х . В итоге у нас получится:

Если обозначить (2/5) х новой переменной y, получим квадратное неравенство:

Неравенства, решаемые графическим методом

Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.

Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.

Пример 1

2 х х и 3 — х, а также точка их пересечения.

Очевидно, что точкой пересечения является х = 1, при этом график функции 2 х ниже в области от -∞ до 1.

Пример 2

Начертим графики этих двух функций, чтобы найти точку пересечения.

Искомой точкой будет х = -1, а областью, где функция (1/2) х находится выше — диапазон от -∞ до -1.