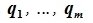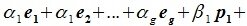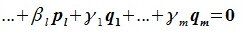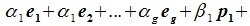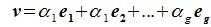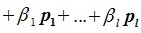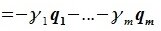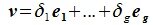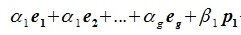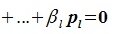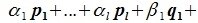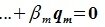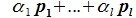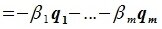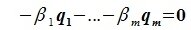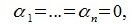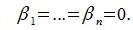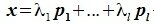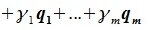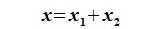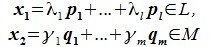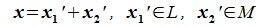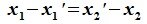Пространство и подпространство линейных уравнений

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.

Линейное пространство

Определения

Пусть дано множество $ \mathbb V_<>=\left\ < X,Y,Z,U,\dots \right\>$ элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения $ X+Y_<> $ и умножения на любое вещественное число $ \alpha_<> $: $ \alpha \cdot X_<> $, и множество $ \mathbb V_<> $ замкнуто относительно этих операций: $ X+Y \in \mathbb V ,\ \alpha \cdot X \in \mathbb V_<> $. Пусть эти операции подчиняются аксиомам:

1. $ X+Y=Y+X_<> $ для $ \ < X,\, Y\>\subset \mathbb V_<> $;

2. $ (X+Y)+Z_<>=X+(Y+Z) $ для $ \ < X,\, Y,\, Z \>\subset \mathbb V_<> $;

3. в $ \mathbb V_<> $ cуществует нулевой вектор $ \mathbb O_<> $ со свойством $ X+ \mathbb O =X_<> $ для $ \forall X\in \mathbb V_<> $;

4. для каждого $ X\in \mathbb V_<> $ существует обратный вектор $ X^<\prime>\in \mathbb V_<> $ со свойством $ X+X^<\prime>=\mathbb O_<> $;

5. $ 1\cdot X=X_<> $ для $ \forall X\in \mathbb V_<> $;

6. $ \lambda \left(\mu X \right)_<>= \left(\lambda \mu \right)X $ для $ \forall X\in \mathbb V_<> $, $ \ <\lambda ,\, \mu \>\subset \mathbb R_<> $ ;

7. $ (\lambda + \mu)X=\lambda X + \mu X_<> $ для $ \forall X\in \mathbb V_<> $, $ \<\lambda ,\, \mu \>\subset \mathbb R_<> $ ;

8. $ \lambda (X + Y) =\lambda X_<> + \lambda Y $ для $ \ < X,\, Y\>\subset \mathbb V_<> , \lambda \in \mathbb R $.

Тогда такое множество $ \mathbb V_<> $ называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из $ \mathbb R_<> $ — последние называются скалярами 1) . Пространство, состоящее из одного только нулевого вектора, называется тривиальным .

Элементарно доказывается единственность нулевого вектора, и единственность вектора, обратного вектору $ X\in \mathbb V_<> $: $ X^<\prime>=-1\cdot X_<> $, его привычно обозначают $ — X_<> $.

Подмножество $ \mathbb V_ <1>$ линейного пространства $ \mathbb V_<> $, само являющееся линейным пространством (т.е. $ \mathbb V_ <1>$ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ \mathbb V_<> $. Тривиальными подпространствами линейного пространства $ \mathbb V_<> $ называются само $ \mathbb V_<> $ и пространство, состоящее из одного нулевого вектора $ \mathbb O_<> $.

Примеры линейных пространств

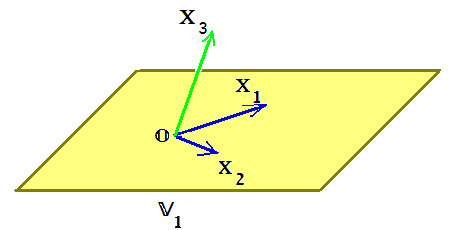
Пример 1. Пространство $ \mathbb R^ <3>$ упорядоченных троек вещественных чисел $ (a_1,a_2,a_<3>) $ с операциями, определяемыми равенствами:

$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3),\ \alpha (a_1,a_2,a_3) = ( \alpha a_1, \alpha a_2, \alpha a_3 ) \ . $$ Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_<3>) $. На рисунке показано и типичное подпространство пространства $ \mathbb R^ <3>$: плоскость, проходящая через начало координат. 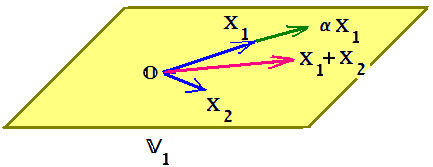Точнее говоря, элементами $ \mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения 2) очевидна.

Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ \mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор» 3) ) — оно определяет набор «сдвигов» точек пространства $ \mathbb R^ <3>$. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ \mathbb V_1 $.

Пример 3. Естественным обобщением $ \mathbb R^ <3>$ служит пространство $ \mathbb R_<>^ $: векторное пространство строк $ (a_1,\dots,a_) $ или столбцов $ (a_1,\dots,a_n)^ <^\top>$. Один из способов задания подпространства в $ \mathbb R_<>^ $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:

$$ \left\<\begin a_<11>x_1 +a_<12>x_2+\ldots+a_<1n>x_n &=&0,\\ a_<21>x_1 +a_<22>x_2+\ldots+a_<2n>x_n &=&0,\\ \ldots& & \ldots \\ a_x_1 +a_x_2+\ldots+a_x_n &=&0 \end\right. \iff AX=\mathbb O $$ образует линейное подпространство пространства $ \mathbb R_<>^ $. В самом деле, если $$x_1=\alpha_1,\dots, x_n=\alpha_n $$ — решение системы, то и $$x_1=t \alpha_1,\dots, x_n= t \alpha_n $$ — тоже решение при любом $ t \in \mathbb R $. Если $$x_1=\beta_1,\dots, x_n=\beta_n $$ — еще одно решение системы, то и $$x_1=\alpha_1+\beta_1,\dots,x_n=\alpha_n+\beta_n $$ — тоже будет ее решением.

Почему множество решений системы неоднородных уравнений не образует линейного подпространства?

Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей $ (a_1,\dots,a_n, \dots ) $, обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ \_ $ удовлетворяющие — при произвольных числах $ \ \> \subset \mathbb R $ — линейному однородному разностному уравнению $ n_<> $-го порядка, $$ x_=a_1 x_+ \dots+ a_n x_K \ npu \ K \in \ <0,1,2,\dots \>\ ; $$ здесь числа $ \< a_1,\dots,a_, a_n \ne 0 \> \subset \mathbb R $ считаются фиксированными.

Можно рассматривать строки (последовательности) «бесконечные в обе стороны» $ \< \dots,a_<-2>,a_<-1>,a_0,a_1,a_2,\dots \> $ — они используются в ТЕОРИИ СИГНАЛОВ.

Пример 5. Множество $ m\times n_<> $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ \mathbb R^ $.

В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.

Пример 6. Множество полиномов одной переменной $ x_<> $ степени в точности равной $ n_<> $ с коэффициентами из $ \mathbb A_<> $ (где $ \mathbb A_<> $ — любое из множеств $ \mathbb Z, \mathbb Q, \mathbb R_<> $ или $ \mathbb C_<> $) с обычными операциями сложения полиномов и умножения на число из $ \mathbb A_<> $ не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов $ f(x)=x^n -x+1 $ и $ g(x)=-x^n+x^-2 $ не будет полиномом $ n_<> $-й степени. Но вот множество полиномов степени не выше $ n_<> $ $$ \mathbb P_n= \left\ < p(x) \in \mathbb A [x] \big| \deg p(x) \le n \right\>$$ линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином 4) . Очевидными подпространствами $ \mathbb P_ $ являются $ \mathbb P_<0>, \mathbb P_1,\dots,\mathbb P_ $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_<> $. Множество всевозможных полиномов $$ \mathbb P= \bigcup_^ <\infty>\mathbb P_n $$ (без ограничения на степени) тоже образует линейное пространство.

Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,\dots, x_ <\ell>$ степени не выше $ n_<> $ с коэффициентами из $ \mathbb A_<> $. Например, множество линейных полиномов $$ \left\< a_1x_1+\dots+a_<\ell>x_<\ell>+b \big| (a_1,\dots,a_<\ell>,b) \in \mathbb A^ <\ell+1>\right\> $$ образует линейное пространство. Множество однородных полиномов (форм) степени $ n_<> $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.

Изоморфизм

Пусть имеются два линейных пространства разной природы: $ \mathbb V_<> $ с операцией $ +_<> $ и $ \mathbb W_<> $ с операцией $ \boxplus_<> $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.

Говорят, что пространства $ \mathbb V_<> $ и $ \mathbb W_<> $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_<> \leftrightarrow X^ <\prime>$ и $ Y_<> \leftrightarrow Y^ <\prime>$ то $ X+Y \leftrightarrow X_<>^ <\prime>\boxplus Y^ <\prime>$ и $ \lambda X_<> \leftrightarrow \lambda X^ <\prime>$.

При изоморфизме пространств $ \mathbb V_<> $ и $ \mathbb W_<> $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.

Пример. Пространство $ \mathbb R^_<> $ изоморфно пространству $ \mathbb P_^<> $. В самом деле, изоморфизм устанавливается соответствием $$ [a_1,\dots,a_n] \leftrightarrow a_1+a_2x+\dots + a_nx^ \ .$$

Пример. Пространство $ \mathbb R^ $ вещественных матриц порядка $ m_<>\times n $ изоморфно пространству $ \mathbb R_<>^ $. Изоморфизм устанавливается с помощью операции векторизации матрицы (матрица «вытягивается» в один столбец).

Пример. Пространство квадратичных форм от $ n_<> $ переменных изоморфно пространству симметричных матриц $ n_<> $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_<> $:

$$ a_<11>x_1^2+a_<12>x_1x_2+a_<13>x_1x_3+a_<22>x_2^2+a_<23>x_2x_3+a_<33>x_3^2 \leftrightarrow \left( \begin a_ <11>& \frac<1><2>a_ <12>& \frac<1><2>a_ <13>\\ \frac<1><2>a_ <12>& a_ <22>& \frac<1><2>a_ <23>\\ \frac<1><2>a_ <13>& \frac<1><2>a_ <23>& a_ <33>\end \right) \ . $$

Линейная зависимость, базис, координаты

Линейной комбинацией системы векторов $ \\> $ называется произвольный вектор $$ \alpha_1 X_1+\dots+ \alpha_m X_m $$ при каких-то фиксированных значениях скаляров $ \alpha_<1>, \dots, \alpha_ $.

Множество всевозможных линейных комбинаций системы векторов $ \\> $ $$ \left\< \alpha_1 X_1+\dots+ \alpha_m X_m \bigg| \<\alpha_1,\dots,\alpha_m\>\subset \mathbb R \right\> $$ называется линейной оболочкой векторов $ X_1,\dots,X_ $ и обозначается $ <\mathcal L>(X_1,\dots,X_) $.

Теорема 1. Линейная оболочка векторов $ X_1,\dots,X_ $ образует линейное подпространство пространства $ \mathbb V_<> $.

Пример. В пространстве $ \mathbb P_ $ полиномов степеней $ \le n_<> \ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида $ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ \le 3 $, имеющих корень $ \lambda_<>=0 $. ♦

Система векторов $ \< X_<1>,\dots,X_m \> $ называется линейно зависимой (л.з.) если существуют числа $ \alpha_<1>,\dots,\alpha_m $, такие что хотя бы одно из них отлично от нуля и $$ \alpha_1X_1+\dots+\alpha_mX_m=\mathbb O $$ Если же это равенство возможно только при $ \alpha_<1>=0,\dots,\alpha_m=0 $, то система векторов называется линейно независимой (л.н.з.).

Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)

$$ f_1=(x_1+x_2+x_3)^2,\quad f_2=x_1x_2+x_1x_3+x_2x_3,\quad f_3=x_1^2+x_2^2+x_3^2 $$ являются линейно зависимыми, поскольку $$ f_1-2\,f_2-f_3 \equiv 0 \ . $$ Полиномы $$ \tilde f_1=x_1+x_2+x_3,\quad f_2=x_1x_2+x_1x_3+x_2x_3,\quad f_3=x_1^2+x_2^2+x_3^2 $$ не являются линейно зависимыми, но являются функционально зависимыми, поскольку $$ \tilde f_1^2-2\,f_2-f_3 \equiv 0 \ . $$ ♦

Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.

б) Если система л.н.з., то и любая ее подсистема л.н.з.

в) При $ m>1 $ система $ \,\dots,X_m\> $ л.з. тогда и только тогда, когда по меньшей мере один ее вектор линейно выражается через остальные, т.е. существуют $ j\in \ <1,\dots,n \>$ и константы $ \gamma_<1>,\dots,\gamma_, \gamma_,\dots,\gamma_ $ такие, что $$ X_j=\gamma_1X_1+\dots+\gamma_X_+ \gamma_X_+\dots + \gamma_X_ .$$

Теорема 3. Если каждый из векторов системы $ \ < X_1,\dots,X_\> $ линейно выражается через векторы другой системы $ \< B_<1>,\dots,B_k \> $ с меньшим числом векторов: $ k ☞ ЗДЕСЬ.

Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.

Теорема 4. Системы векторов

$$ \ < X_1,\dots,X_\> \quad \mbox < и >\quad \< Y_<1>,\dots,Y_k \> $$ будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем: $$<\mathcal L>(X_1,\dots,X_m)=<\mathcal L>(Y_1,\dots,Y_k) \ . $$

Теорема 5. Если каждая из двух эквивалентных систем

$$ \ < X_1,\dots,X_\> \quad \mbox < и >\quad \< Y_<1>,\dots,Y_k \> $$ является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_<> $ .

Линейно независимая система векторов $ \\>\subset \mathbb V $ называется базисом этого пространства если каждый $ X\in \mathbb V $ можно представить в виде линейной комбинации указанных векторов: $$ X=\sum_ \alpha_j X_j \ . $$

При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ \left[a_<1>,a_2,\dots\, \right] $ имеет бесконечный базис, состоящий из векторов $$ [\underbrace<0,\dots,0,1>_j,0,\dots \, ] \quad npu \ j \in \mathbb N \ . $$

В случае, когда базис пространства $ \mathbb V_<> $ конечен, пространство $ \mathbb V_<> $ называется конечномерным, а число векторов базиса тогда называется размерностью пространства $ \mathbb V_<> $ и обозначается 5) : $ \dim \mathbb V_<> $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ \dim \ <\mathbb O_<>\>= 0 $.

Пример. Линейное пространство $ m\times n_<> $ матриц имеет размерность $ mn_<> $. Так, для случая $ m_<>=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц

$$ \left( \begin 1 & 0 \\ 0 & 0 \\ 0 & 0 \end \right) \ , \ \left( \begin 0 & 1 \\ 0 & 0 \\ 0 & 0 \end \right) \ , \ \left( \begin 0 & 0 \\ 1 & 0 \\ 0 & 0 \end \right) \ , \left( \begin 0 & 0 \\ 0 & 1 \\ 0 & 0 \end \right) \ , \ \left( \begin 0 & 0 \\ 0 & 0 \\ 1 & 0 \end \right) \ , \ \left( \begin 0 & 0 \\ 0 & 0 \\ 0 & 1 \end \right) \ . $$ ♦

Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_<> $.

Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

под умножением цвета на положительное число $ k_<> $ — увеличение в $ k_<> $ раз яркости цвета

Анимация ☞ ЗДЕСЬ (1500 K, gif)

под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения. ♦

Если $ \dim \mathbb V=d_<> $ и вектора $ X_1,\dots,X_ $ являются базисными для $ \mathbb V_<> $, то разложение вектора $ X \in \mathbb V_<> $ в сумму: $$ X=\alpha_1 X_1+\dots+ \alpha_d X_d \ .$$ называется разложением вектора $ X_<> $ по базису $ X_1,\dots,X_ $; при этом числа $ \alpha_1,\dots, \alpha_ $ называются координатами вектора $ X_<> $ в данном базисе.

Теорема 6. Если $ \dim \mathbb V=d>0 $, то любая система из $ d_<> $ линейно независимых векторов пространства образует базис этого пространства.

Доказательство. Пусть $ \ $ — л.н.з. система. Рассмотрим произвольный $ X\in \mathbb V_<> $. Если система $ \ $ л.н.з., то $ \dim \mathbb V \ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно зависима: $ \alpha_0X+\alpha_1Y_1+\dots+\alpha_dY_d=\mathbb O $ при каком-то из чисел $ \<\alpha_j\>_^ $ не равном нулю. Если $ \alpha_0=0 $, то $ \alpha_1Y_1+\dots+\alpha_dY_d=\mathbb O $ при каком-то ненулевом коэффициенте. Это означает, что система $ \ $ линейно зависима, что противоречит предположению. Следовательно $ \alpha_0\ne 0 $, но тогда вектор $ X_<> $ может быть представлен в виде линейной комбинации векторов $ Y_1,\dots,Y_d $: $$X=- <\alpha_1>/ <\alpha_0>Y_1-\dots —<\alpha_d>/<\alpha_0>Y_d \ .$$ По определению, система $ \ $ является базисом $ \mathbb V $. ♦

Теорема 7. Любой вектор $ X \in \mathbb V_<> $ может быть разложен по фиксированному базису пространства единственным образом.

Очевидно, $ \dim \mathbb R^ = n $: строки из $ n_<> $ элементов $$[1,0,0,\dots,0],\ [0,1,0,\dots,0],\ [0,0,1,\dots,0],\ \dots , [0,0,0,\dots,1] $$ образуют базис этого пространства.

Имеются два способа задания линейных подпространств в $ \mathbb R^_<> $. Пусть $$ \mathbb V_1 = <\mathcal L>(A_1,\dots,A_k) \quad npu \ \ \subset \mathbb R^n \ .$$ В разделе ☞ РАНГ установлено, что $$ \dim \mathbb V_1 = \operatorname \ < A_1,\dots,A_k \>= \operatorname (A) \ ,$$ где $ A_<> $ — матрица, составленная из строк (столбцов) $ A_<1>,\dots,A_k $.

Пример. Найти базис подпространства

Решение. Ищем $$ \operatorname \left( \begin 1 & 2 & 1 & 1 \\ -1&0&-1&0 \\ -1& 2 &-1 &1 \\ 0& 1& 0 & 1 \end \right) $$ по методу окаймляющих миноров. Существует минор третьего порядка $$ \left| \begin 1 & 2 & 1 \\ -1&0&0 \\ 0& 1 & 1 \end \right| $$ отличный от нуля, а определитель самой матрицы равен нулю. Замечаем, что найденный отличный от нуля минор расположен в первой, второй и четвертой строках матрицы. Именно эти строки и образуют базис.

Ответ. Базис составляют, например, первая, вторая и четвертая строки.

Другим способом задания линейного подпространства в $ \mathbb R^ $ может служить задание набора ограничений, которым должны удовлетворять векторы подпространства. Таким набором ограничений может являться, например, система уравнений $$ \left\<\begin a_<11>x_1 +a_<12>x_2+\ldots+a_<1n>x_n &=&0,\\ a_<21>x_1 +a_<22>x_2+\ldots+a_<2n>x_n &=&0,\\ \ldots& & \ldots \\ a_x_1 +a_x_2+\ldots+a_x_n &=&0 \end\right. \qquad \iff \qquad AX=\mathbb O . $$ Какова размерность подпространства решений этой системы? На этот вопрос мы ответим сразу же, если вспомним определение фундаментальной системы решений (ФСР). Именно, ФСР — как набор линейно независимых решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.

Теорема 8. Множество решений системы однородных уравнений $ AX=\mathbb O_<> $ образует линейное подпространство пространства $ \mathbb R^ $. Размерность этого подпространства равна $ n-\operatorname (A) $, а фундаментальная система решений образует его базис.

Пример. В пространстве $ \mathbb P_ $ полиномов степеней $ \le n_<> $ каноническим базисом можно взять систему мономов $ \ <1,x,x^2,\dots, x^n \>$, т.е. $ \dim \mathbb P_ =n+1 $. Координатами полинома

$$ f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например, $ \ <1, x-c,(x-c)^2,\dots,(x-c)^n \>$ при произвольном числе $ c_<> $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора: $$ f(x) \equiv f(c)+ \frac(c)> <1!>(x-c) + \frac(c)> <2!>(x-c)^2+ \dots + \frac(c)> (x-c)^ \ . $$

Найти координаты полинома

Теорема 9. Любое векторное пространство $ \mathbb V_<> $ размерности $ d_<> $ изоморфно $ \mathbb R^ $.

Доказательство. Изоморфизм можно установить следующим соответствием. Если $ \ $ — какой-то базис $ \mathbb V_<> $, то вектору $ X \in \mathbb V $ поставим в соответствие набор его координат в этом базисе: $$ X=x_1X_1+\dots+x_d X_d \ \Rightarrow \ X \mapsto [x_1,\dots,x_d]\in \mathbb R^d . $$ На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным, а проверка двух свойств изоморфизма тривиальна. ♦

Критерии линейной зависимости

Теорема . Строки

$$ \<(a_<11>,\dots,a_<1n>),\dots, (a_,\dots,a_)\> \subset \mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ \left|\begin a_<11>&\dots & a_ <1n>\\ \dots & & \dots \\ a_& \dots & a_ \end \right|=0 \, . $$

Теорема . Строки

$$ \<(a_<11>,\dots,a_<1n>),\dots, (a_,\dots,a_)\> \subset \mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ \operatorname A

$$ \<(a_<11>,\dots,a_<1n>),\dots, (a_,\dots,a_)\> \subset \mathbb R^n $$ линейно зависимы тогда и только тогда, когда $$ \det (A^ <\top>A) = 0 \, . $$ (Определитель в левой части можно интерпретировать как определитель Грама системы строк.)

Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),\dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан

Относительный базис

В настоящем пункте $ \mathbb V_1 $ обозначает линейное подпространство пространства $ \mathbb V_<> $, отличное от тривиального; обозначаем $ d_1=\dim \mathbb V_1 $.

Теорема. Произвольный базис подпространства $ \mathbb V_1 $ можно дополнить до базиса пространства $ \mathbb V_<> $.

Доказательство. Пусть $ \ \> $ — какой-то базис $ \mathbb V_1 $. В пространстве $ \mathbb V_<> $ найдется вектор $ X_ $ такой, что система $ \, X_\> $ будет л.н.з. (В противном случае, $ \dim \mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если $ d_1+1=d = \dim \mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый базис построен. Если же $ d_1+1 ♦

Говорят, что система векторов $ \ $ линейно независима относительно подпространства $ \mathbb V_1 $ пространства $ \mathbb V_<> $ если $$<.>_<> \mbox < из условия >\quad \alpha_1X_1+\dots+\alpha_k X_k \in \mathbb V_1 \quad \mbox < следует >\quad \alpha_1=\dots=\alpha_k=0 \ .$$

Теорема. Обозначим $ \\> $ — произвольный базис $ \mathbb V_1 $. Система $ \,\dots,X_k\> $ л.н.з. относительно $ \mathbb V_1 $ тогда и только тогда, когда система $ \,X_1,\dots,X_k\> $ линейно независима.

Пример. Найти все значения параметра $ <\color\alpha > $, при которых система

Решение. Базисом подпространства $ \mathbb V_1 $ является произвольная ФСР заданной системы однородных уравнений, например $ \>,\ Y_2=[6,-5,0,1]^<^<\top>>\> $. Теорема утверждает, что система $ \ < X_1, X_2\>$ л.н.з. относительно $ \mathbb V_1 $ тогда и только тогда, когда система $ \ < X_1, X_2,Y_1,Y_2\>$ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная из этих векторов, должна иметь ранг равный $ 4_<> $. $$\operatorname \left( \begin 1 & 1 &-1 & 6 \\ 2 & \ <\color\alpha > & 2 & -5 \\ <\color\alpha > & 2 & 1 & 0 \\ 1 & 1 & 0 & 1 \end \right)=4 \ \iff \ \left| \begin 1 & 1 &-1 & 6 \\ 2 & <\color\alpha > & 2 & -5 \\ <\color\alpha > & 2 & 1 & 0 \\ 1 & 1 & 0 & 1 \end \right|= <\color\alpha >^2-10\, <\color\alpha > +16 \ne 0 \ . $$

Ответ. $ <\color\alpha >\not \in \ < 2,\, 8\>$.

Говорят, что система векторов $ \ $ образует базис пространства $ \mathbb V_<> $ относительно (или над) $ \mathbb V_1 $ если она л.н.з. относительно $ \mathbb V_1 $ и любой вектор $ X\in \mathbb V_<> $ можно представить в виде $$ X=c_1X_1+\dots+c_kX_k+Y, \quad \mbox < где >\quad Y\in \mathbb V_1 \ . $$

Теорема. Обозначим $ \ < Y_1,\dots,Y_\> $ — произвольный базис подпространства $ \mathbb V_1 $. Система $ \ $ образует базис $ \mathbb V_<> $ относительно $ \mathbb V_1 $ тогда и только тогда, когда система $ \ < X_1,\dots,X_k,Y_1,\dots,Y_\> $ образует базис $ \mathbb V_<> $.

Доказательство. Действительно, любой вектор $ X\in \mathbb V_<> $ выражается через векторы $ X_1,\dots,X_k,Y_1,\dots,Y_ $. По предыдущей теореме для линейной независимости этих векторов необходимо и достаточно относительной линейной независимости $ X_1,\dots,X_k $. ♦

Базис $ \mathbb V_<> $ строится дополнением базиса $ \mathbb V_1 $ векторами $ X_1,\dots,X_k $ линейно независимыми относительно $ \mathbb V_1 $. Поэтому $$<.>_<> \mbox <число векторов относительного базиса >\ = \dim \mathbb V — \dim \mathbb V_1 \ .$$

Это число называется коразмерностью 6) подпространства $ \mathbb V_1 $ в пространстве $ \mathbb V $.

Сумма и пересечение линейных подпространств

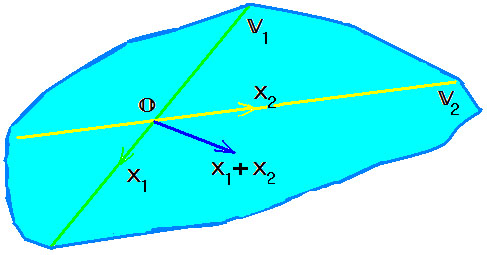
Пусть $ \mathbb V_1 $ и $ \mathbb V_2 $ — подпространства линейного пространства $ \mathbb V_<> $. Множество $$ \mathbb V_1+ \mathbb V_2 = \left\$$ называется суммой, а множество $$ \mathbb V_1 \cap \mathbb V_2 = \left\$$ — пересечением подпространств $ \mathbb V_1 $ и $ \mathbb V_2 $. Аналогично определяется сумма и пересечение произвольного количества подпространств.

Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.

Теорема. $ \mathbb V_1+ \mathbb V_2 $ и $ \mathbb V_1 \cap \mathbb V_2 $ являются подпространствами линейного пространства $ \mathbb V_<> $.

Докажите, что $ \mathbb V_1+ \mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ \mathbb V_1 $, так и $ \mathbb V_2 $.

Теорема. Имеет место формула:

$$ \dim \, \mathbb V_1 + \dim \, \mathbb V_2=\dim \, (\mathbb V_1 \cap \mathbb V_2) + \dim \, (\mathbb V_1 + \mathbb V_2) \ . $$

Доказательство ☞ ЗДЕСЬ.

Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:

$$\dim \, \mathbb V_1 + \dim \, \mathbb V_2 + \dim \, \mathbb V_3 — $$ $$ -\left\ <\dim \, (\mathbb V_1 \cap \mathbb V_2) + \dim \, (\mathbb V_1 \cap \mathbb V_3) + \dim \, (\mathbb V_2 \cap \mathbb V_3) \right\>+ $$ $$+ \dim \, (\mathbb V_1 \cap \mathbb V_2 \cap \mathbb V_3) =\dim \, (\mathbb V_1 + \mathbb V_2 + \mathbb V_3) \ ?$$

Теорема. Имеет место формула:

Пример. Найти базис суммы и размерность пересечения

$$\mathbb V_1=<\mathcal L>\left( \left[ \begin 0 \\1 \\ 1 \\ 1 \end \right] , \left[ \begin 1 \\1 \\ 1 \\ 2 \end \right] , \left[ \begin -2 \\0 \\ 1 \\ 1 \end \right] \right) \quad \mbox < и >\quad \mathbb V_2=<\mathcal L>\left( \left[ \begin -1 \\3 \\ 2 \\ -1 \end \right] , \left[ \begin 1 \\1 \\ 0 \\ -1 \end \right] \right) $$

Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов $$ \left( \begin 0 & 1 & -2 & -1 & 1 \\ 1 & 1 & 0 & 3 & 1 \\ 1 & 1 & 1 & 2 & 0 \\ 1 & 2 & 1 & -1 & -1 \end \right) $$ и ищем ее ранг методом окаймляющих миноров. Имеем: $ \operatorname = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.

Ответ. Базис $ \mathbb V_1 + \mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $; $ \dim \, (\mathbb V_1 \cap \mathbb V_2) = 3+2 — 3 =2 $.

Алгоритм нахождения базиса $ <\mathcal L>(X_1,\dots,X_m) \cap <\mathcal L>(Y_1,\dots,Y_<\ell>) $ проиллюстрируем на примере.

Пример. Найти базис $ \mathbb V_1 \cap \mathbb V_2 $ при

$$ \begin \mathbb V_1= <\mathcal L>\left( \left[ \begin 1 \\ -1 \\ 1 \\ -1 \\ 1 \end \right],\, \left[ \begin 1 \\ 2 \\ 1 \\ 2 \\ 1 \end \right],\, \left[ \begin 0 \\ 1 \\ 0 \\ 1 \\ 0 \end \right] \right) \\ <>_<> \qquad \qquad \quad X_1 \quad \quad \ X_2 \quad \quad X_3 \end ,\ \begin \mathbb V_2= <\mathcal L>\left( \left[ \begin 1 \\ 0 \\ 0 \\ 0 \\ 1 \end \right],\, \left[ \begin 1 \\ 1 \\ 0 \\ 1 \\ 1 \end \right],\, \left[ \begin 0 \\ 1 \\ 1 \\ 1 \\ 0 \end \right] \right) \\ <>_<> \quad \qquad \qquad Y_1 \qquad \ Y_2 \quad \quad Y_3 \end \ . $$

Решение. 1. Сначала найдем базисы каждого из подпространств: $$\dim \mathbb V_1=2, \ \mathbb V_1=\mathcal L(X_1, X_2) \ ; \ \dim \mathbb V_2=3,\ \mathbb V_2=\mathcal L(Y_1, Y_2, Y_3) \ . $$

2. Произвольный вектор $ Z\in \mathbb R^5 $, принадлежащий $ \mathbb V_1 \cap \mathbb V_2 $, должен раскладываться по базису каждого из подпространств: $$Z=\alpha_1 X_1 + \alpha_2 X_2= \beta_1 Y_1 + \beta_2 Y_2 + \beta_3 Y_3 \ .$$ Для определения неизвестных значений координат составляем систему уравнений $$ \begin \qquad X_1 \ X_2 \\ \qquad <\color\downarrow> \ \ \ <\color\downarrow> \\ \left( \begin 1 & 1 & -1 & &-1 & & \ 0 \\ -1 & 2 & 0 & & -1 & & \ -1 \\ 1 & 1 & 0 & & 0 & & \ -1 \\ -1 & 2 & 0 & & -1 & & \ -1 \\ 1 & 1 & -1 & & -1 & &\ 0 \end \right) \\ \qquad \qquad \qquad <\color\uparrow> \qquad \ \ <\color\uparrow> \qquad \quad <\color\uparrow> \\ \quad \qquad \qquad -Y_1 \quad — Y_2 \quad -Y_3 \end \left( \begin \alpha_1 \\ \alpha_2 \\ \beta_1 \\ \beta_2 \\ \beta_3 \end \right)= \mathbb O_ <5\times 1>$$ и решаем ее по методу Гаусса с нахождением фундаментальной системы решений: $$ \left( \begin 1 & 1 & -1 & -1 & 0 \\ 0 & 3 & -1 & -2 & -1 \\ 0 & 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end \right) \left( \begin \alpha_1 \\ \alpha_2 \\ \beta_1 \\ \beta_2 \\ \beta_3 \end \right)= \mathbb O \quad \Rightarrow \qquad \mbox < ФСР >\qquad \begin \alpha_1 & \alpha_2 & \beta_1 & \beta_2 & \beta_3 \\ \hline -1/3 & 1/3 & -1 & 1 & 0 \\ 1/3 & 2/3 & 1 & 0 & 1 \end $$

3. Получившиеся значения координат позволяют выразить базис пересечения — либо через базис подпространства $ \mathbb V_1 $ (если использовать полученные значения для $ \alpha_1,\alpha_2 $), либо через базис подпространства $ \mathbb V_2 $ (если использовать $ \beta_1,\beta_2, \beta_3 $). Например, $$ Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^<^<\top>>,\ $$ $$ Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^<^<\top>> \ . $$

Найти базисы суммы и пересечения подпространств

Решение ☞ ЗДЕСЬ.

Прямая сумма линейных подпространств

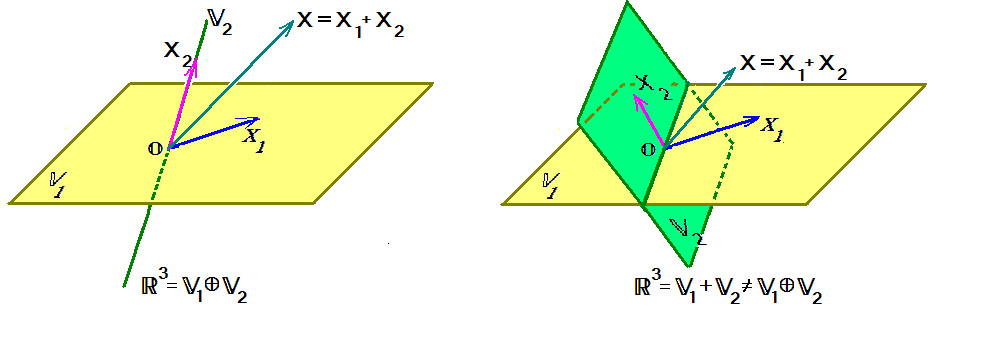
Пусть $ \mathbb V_1 $ и $ \mathbb V_2 $ — подпространства линейного пространства $ \mathbb V_<> $. Говорят, что $ \mathbb V_<> $ раскладывается в прямую сумму подпространств $ \mathbb V_1 $ и $ \mathbb V_2 $ если любой вектор $ X\in \mathbb V_<> $ может быть представлен в виде $ X=X_1+X_2 $, где $ X_1\in \mathbb V_1,X_2\in \mathbb V_2 $ и такое представление единственно. Этот факт записывают: $ \mathbb V= \mathbb V_1 \oplus \mathbb V_2 $. Вектор $ X_ <1>$ называется проекцией вектора $ X_<> $ на подпространство $ \mathbb V_1 $ параллельно подпространству $ \mathbb V_ <2>$.

Пример. Линейное пространство квадратных матриц порядка $ n_<> $ раскладывается в прямую сумму подпространств: подпространства симметричных матриц и подпространства кососимметричных матриц. В самом деле, для матрицы $ A_ $ справедливо разложение

$$A=\frac<1> <2>\left(A+A^ <^\top>\right) + \frac<1> <2>\left(A-A^ <^\top>\right) $$ и в правой части первая скобка дает симметричную матрицу, а вторая — кососимметричную. Покажите, что не существует иного разложения матрицы $ A_<> $ в сумму симметричной и кососимметричной.

Теорема. Пусть $ \mathbb V=\mathbb V_1 + \mathbb V_2 $. Эта сумма будет прямой тогда и только тогда, когда подпространства $ \mathbb V_1 $ и $ \mathbb V_2 $ имеют тривиальное пересечение:

$$\mathbb V_1 \cap \mathbb V_2=\ <\mathbb O \>\ .$$

Доказательство. Необходимость. Пусть сумма $ \mathbb V_1 + \mathbb V_2 $ — прямая, но существует вектор $ X\ne \mathbb O $, принадлежащий $ \mathbb V_1 \cap \mathbb V_2 $. Но тогда и вектор $ (-X) $ принадлежит $ \mathbb V_1 \cap \mathbb V_2 $. Для нулевого вектора $ \mathbb O $ получаем два представления в виде суммы проекций на подпространства: $$ \mathbb O = \mathbb O + \mathbb O = X+ (-X) \, . $$ Это противоречит понятию прямой суммы.

Достаточность. Если $ \mathbb V_1 \cap \mathbb V_2=\ <\mathbb O \>$, но существует вектор $ X \in \mathbb V_1 + \mathbb V_2 $, имеющий два различных разложения в сумму проекций $$ X=X_1+X_2 =Y_1+ Y_2 \quad npu \quad \ \subset \mathbb V_1, \ \ \subset \mathbb V_2, $$ то $$ (X_1-Y_1)+(X_2-Y_2) =\mathbb O \quad \Rightarrow \quad X_1-Y_1=Y_2-X_2 \, , $$ т.е. вектор $ X_1-Y_1 $ принадлежит $ \mathbb V_1 \cap \mathbb V_2 $. Но, по предположению, $ \mathbb V_1 \cap \mathbb V_2=\ <\mathbb O \>$, следовательно, $ X_1-Y_1=\mathbb O $, но тогда и $ Y_2-X_2=\mathbb O $. ♦

Сумма $ \mathbb V=\mathbb V_1 + \mathbb V_2 $ будет прямой тогда и только тогда, когда базис $ \mathbb V_<> $ может быть получен объединением базисов $ \mathbb V_ $.

Пример [2]. Доказать, что сумма подпространств

$$\mathbb V_1=<\mathcal L>\left( \left[ \begin 2 \\3 \\ 11 \\ 5 \end \right] , \left[ \begin 1 \\1 \\ 5 \\ 2 \end \right] , \left[ \begin 0 \\1 \\ 1 \\ 1 \end \right] \right) \quad \mbox < и >\quad \mathbb V_2=<\mathcal L>\left( \left[ \begin 2 \\1 \\ 3 \\ 2 \end \right] , \left[ \begin 1 \\1 \\ 3 \\ 4 \end \right] , \left[ \begin 5 \\2 \\ 6 \\ 2 \end \right] \right) $$ будет прямой и найти проекции вектора $ Z=[2,0,0,3]^ <\top>$ на эти подпространства.

Решение. Базисы $ \mathbb V_1 $ и $ \mathbb V_2 $ составляют соответственно системы $ \ $ и $ \ < Y_1,Y_2 \>$, т.е. $ \dim \, \mathbb V_1=\dim \, \mathbb V_2 =2 $. На основании следствия достаточно установить, что объединенная система $ \ $ л.н.з. Для этого достаточно проверить, что определитель матрицы $$ A=\left( \begin 1 & 0 & 2 & 1 \\ 1 & 1 & 1 & 1 \\ 5 & 1 & 3 & 3 \\ 2 & 1 & 2 & 4 \end \right) $$ отличен от нуля. Поскольку это условие выполнено, то сумма $ \mathbb V_1 + \mathbb V_2 $ — прямая и базис этой суммы состоит из взятых векторов. Для нахождения разложения вектора $ X_<> $ по этому базису решаем систему уравнений $$A \left[ \begin \alpha_2 \\ \alpha_3 \\ \beta_1 \\ \beta_2 \end \right] = Z $$ и получаем единственное решение: $ \alpha_2=-1,\, \alpha_3=-1,\, \beta_1 =1\, , \beta_2=1 $. Разложение $ Z=Z_1+Z_2 $ составляют векторы $ Z_1=\alpha_2 X_2+\alpha_3 X_3 $ и $ Z_2=\beta_1 Y_1+\beta_2 Y_2 $.

Линейные многообразия

Пусть $ \mathbb V_1 $ — линейное подпространство пространства $ \mathbb V_<> $, а $ X_ <0>$ — произвольный фиксированный вектор из $ \mathbb V_<> $. Множество $$ \mathbb M = X_0+ \mathbb V_1 = \left\ $$ называется линейным многообразием (порожденным подпространством $ \mathbb V_1 $). Размерностью этого многообразия называется размерность порождающего его подпространства: $ \dim \mathbb M = \dim \mathbb V_1 $. В случае $ 1 ☞ ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее общее решение можно представить как сумму какого-то одного ее решения и общего решения соответствующей однородной системы $ AX= \mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX= <\mathcal B>$ допускает «параметрическое представление»: $$\mathbb M=X_0+ <\mathcal L>(X_1,\dots,X_>)= $$ $$=\left\> X_> \mid (t_1,\dots, t_>) \in \mathbb R^> \right\> \ ; $$ здесь $ X_ <0>$ означает частное решение системы (т.е. $ AX_0= <\mathcal B>$),

$ \>\> $ — ФСР для системы $ AX= \mathbb O $,

а $ \mathfrak r= \operatorname A= \operatorname [A\mid \mathcal B] $.

Получаем, следовательно, $ (n-<\mathfrak r>) $-мерную плоскость в $ \mathbb R^n $, a в случае $ (n-<\mathfrak r>)=1 $ — прямую $$\mathbb M=X_0+tX_1 \quad npu \ t \in \mathbb R \ ; $$ в последнем случае вектор $ X_ <1>$ называют направляющим вектором этой прямой.

Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Пусть L и M — два подпространства пространства R.

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

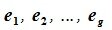
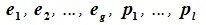
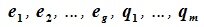
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

Из уравнений (6.4) и (6.5) имеем:

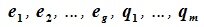
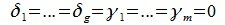
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

В силу линейной независимости базиса подпространства L имеем:

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

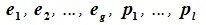
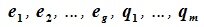
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов а y — линейной комбинацией векторов. Следовательно векторы (6.10) порождают подпространство F. Получили, что векторы (6.10) образуют базис F=L+M.

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

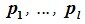
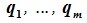
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M= 0, то

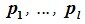
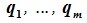
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:

Вычитая (6.19) из (6.17), получим

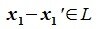
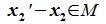
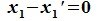
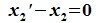
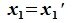
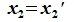
Так как , и L∩M= 0, то и . Следовательно и . ■

Подпространства линейного пространства

Определение линейного подпространства

Непустое подмножество линейного пространства называется линейным подпространством пространства , если

1) (подпространство замкнуто по отношению к операции сложения);

2) и любого числа (подпространство замкнуто по отношению к операции умножения вектора на число).

Для указания линейного подпространства будем использовать обозначение , а слово «линейное» опускать для краткости.

1. Условия 1, 2 в определении можно заменить одним условием: и любых чисел и . Разумеется, что здесь и в определении речь идет о произвольных числах из того числового поля, над которым определено пространство .

2. В любом линейном пространстве имеются два линейных подпространства:

а) само пространство , т.е. ;

б) нулевое подпространство , состоящее из одного нулевого вектора пространства , т.е. . Эти подпространства называются несобственными, а все остальные — собственными.

3. Любое подпространство линейного пространства является его подмножеством: , но не всякое подмножество является линейным подпространством, так как оно может оказаться незамкнутым по отношению к линейным операциям.

4. Подпространство линейного пространства само является линейным пространством с теми же операциями сложения векторов и умножения вектора на число, что и в пространстве , поскольку для них выполняются аксиомы 1-8. Поэтому можно говорить о размерности подпространства, его базисе и т.п.

5. Размерность любого подпространства линейного пространства не превосходит размерности пространства . Если же размерность подпространства равна размерности конечномерного пространства , то подпространство совпадает с самим пространством: .

Это следует из теоремы 8.2 (о дополнении системы векторов до базиса). Действительно, взяв базис подпространства , будем дополнять его до базиса пространства . Если это возможно, то . Если нельзя дополнить, т.е. базис подпространства является базисом пространства , то . Учитывая, что пространство есть линейная оболочка базиса (см. следствие 1 теоремы 8.1), получаем .

6. Для любого подмножества линейного пространства линейная оболочка является подпространством и .

В самом деле, если (пустое множество), то по определению , т.е. является нулевым подпространством и . Пусть . Нужно доказать, что множество замкнуто по отношению к операциям сложения его элементов и умножения его элементов на число. Напомним, что элементами линейной оболочки служат линейные комбинации векторов из . Так как линейная комбинация линейных комбинаций векторов является их линейной комбинацией, то, учитывая пункт 1, делаем вывод, что является подпространством , т.е. . Включение — очевидное, так как любой вектор можно представить как линейную комбинацию , т.е. как элемент множества .

7. Линейная оболочка подпространства совпадает с подпространством , т.е. .

Действительно, так как линейное подпространство содержит все возможные линейные комбинации своих векторов, то . Противоположное включение следует из пункта 6. Значит, .

Примеры линейных подпространств

Укажем некоторые подпространства линейных пространств, примеры которых рассматривались ранее. Перечислить все подпространства линейного пространства невозможно, за исключением тривиальных случаев.

1. Пространство , состоящее из одного нулевого вектора пространства , является подпространством, т.е. .

2. Пусть, как и ранее, — множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно. Если прямая принадлежит плоскости, то . Напротив, множество единичных векторов не является линейным подпространством, так как при умножении вектора на число, не равное единице, получаем вектор, не принадлежащий множеству.

3. В n-мерном арифметическом пространстве рассмотрим множество «полунулевых» столбцов вида с последними элементами, равными нулю. Сумма «полунулевых» столбцов является столбцом того же вида, т.е. операция сложения замкнута в . Умножение «полунулевого» столбца на число дает «полунулевой» столбец, т.е. операция умножения на число замкнута в . Поэтому , причем . Напротив, подмножество ненулевых столбцов не является линейным подпространством, так как при умножении на нуль получается нулевой столбец, который не принадлежит рассматриваемому множеству. Примеры других подпространств приводятся в следующем пункте.

4. Пространство решений однородной системы уравнений с неизвестными является подпространством n-мерного арифметического пространства . Размерность этого подпространства определяется матрицей системы: .

Множество решений неоднородной системы (при ) не является подпространством , так как сумма двух решений неоднородной ; системы не будет решением той же системы.

5. В пространстве квадратных матриц порядка л рассмотрим два подмножества: множество симметрических матриц и множество кососимметрических матриц. Сумма симметрических матриц является симметрической матрицей, т.е. операция сложения замкнута в . Умножение симметрической матрицы на число также не нарушает симметричность, т.е. операция умножения матрицы на число замкнута в . Следовательно, множество симметрических матриц является под пространством пространства квадратных матриц, т.е. . Нетрудно найти размерность этого подпространства. Стандартный базис образуют : л матриц с единственным ненулевым (равным единице) элементом на глав ной диагонали: , а также матрицы с двумя ненулевыми (равными единице) элементами, симметричными относительно главной диагонали: . Всего в базисе будет матриц. Следовательно, . Аналогично получаем, что и .

Множество вырожденных квадратных матриц n-го порядка не является подпространством , так как сумма двух вырожденных матриц может оказаться невырожденной матрицей, например, в пространстве

6. В пространстве многочленов с действительными коэффициентами можно указать естественную цепочку подпространств

Множество четных многочленов является линейным подпространством , так как сумма четных многочленов и произведение четно го многочлена на число будут четными многочленами. Множество нечетных многочленов также является линейным пространством. Множество многочленов, имеющих действительные корни, не является линейным подпространством, так как при сложении таких двух многочленов может получиться многочлен, который не имеет действительных корней, например, .

7. В пространстве можно указать естественную цепочку подпространств:

Многочлены из можно рассматривать как функции, определенные на . Так как многочлен является непрерывной функцией вместе со своими производными любого порядка, можно записать: и . Пространство тригонометрических двучленов является подпространством , так как производные любого порядка функции непрерывны, т.е. . Множество непрерывных периодических функций не является подпространством , так как сумма двух периодических функций может оказаться непериодической функцией, например, .