Педагогические тестовые материалы для проверки знаний студентов по дисциплинам «Вычислительная математика», «численные методы»
Министерство образования Российской Федерации
Владивостокский государственный университет

Филиал в г. Находке
ПЕДАГОГИЧЕСКИЕ ТЕСТОВЫЕ МАТЕРИАЛЫ
ДЛЯ ПРОВЕРКИ ЗНАНИЙ СТУДЕНТОВ
«ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА», «ЧИСЛЕННЫЕ МЕТОДЫ»
Направления: 654700 Информационные системы
350000 Междисциплинарные специальности
Специальности: 220100 Вычислительные машины, комплексы
351400 Прикладная информатика (в экономике)
Министерство образования Российской Федерации
Владивостокский государственный университет
экономики и сервиса
Филиал в г. Находке
ПЕДАГОГИЧЕСКИЕ ТЕСТОВЫЕ МАТЕРИАЛЫ ДЛЯ ПРОВЕРКИ ЗНАНИЙ СТУДЕНТОВ
Направления: 654600 Информатика и вычислительная техника
350000 Междисциплинарные специальности
Специальности: 220100 Вычислительные машины, комплексы,
351400 Прикладная информатика (в экономике)
Печатается по решению ученого совета филиала ВГУЭС в г. Находке.
Авторы – составители: Ф. А. Юн, к. т.н., доцент
Рецензент: зав. Кафедрой математики и информатики НФ ДВГАЭУ,
д-р ф.- м. н, профессор
© Юн Ф. А., , составление, 2003
© Институт технологии и бизнеса, 2003
I. ПЕРЕЧЕНЬ ПЕДАГОГИЧЕСКИХ ТЕСТОВЫХ ЗАДАНИИ
1. Норма матрицы 
а) вектор – строка; б) число; в) вектор – столбец.
2. Норма 2 матрицы 
2. Норма 2 матрицы
а) 30; б) 39; в) 28,6356.
3. Процесс построения значения корней системы с заданной точностью в виде предела последовательности некоторых векторов называется
а) итерационным; б) сходящимся; в) расходящимся.
4. Процесс Зейделя для линейной системы 
к единственному решению при любом выборе начального приближения, если какая-нибудь из норм матрицы
а) больше единицы; б) меньше единицы; в) равна единице.
5. Процесс нахождения приближенных значений корней уравнения разбивается на
а) построение графика и уточнение корней до заданной степени точности;
б) отделение корней и уточнение корней до заданной степени точности;
в) уточнение корней до заданной степени точности и определение
погрешности приближения.
6. Количество действительных положительных корней алгебраического уравнения 
а) Декарта; б) Штурма; в) Лагранжа.
7. Верхняя граница положительных корней уравнения 
а) 


б) 
в) 

8. Интерполяционным многочленом называется многочлен,
а) значения которого в узлах интерполяции равны значению табличной функции в этих узлах;
б) 
в) параболического вида.
9. Конечные табличные разности используются в интерполяционной формуле
а) Гаусса для равноотстоящих узлов интерполяции;
б) Эйткина для равноотстоящих узлов интерполяции;
в) Ньютона для равноотстоящих узлов интерполяции;
г) Лагранжа для равноотстоящих узлов интерполяции.
10. Первый интерполяционный многочлен Лагранжа имеет вид:
а) 
б)

в)
11. Квадратурная формула Гаусса имеет вид
а) 
б) 
в) 
г) 
12. По методу Пикара любое приближение решения дифференциального уравнения определяется по формуле
а) 

б) 
в) 

г) 
д) 

1. Максимальная сумма модулей элементов матрицы по строкам есть
а) норма 2; б) норма 3; в) норма 1.
2. Норма 3 матрицы 
2. Норма 2 матрицы
а) 30; б) 39; в) 28,6356.
3. Итерационный процесс построения приближений по формуле 
а) методом Зейделя;
б) методом Ньютона;
в) методом итерации.
4. Процесс Зейделя для линейной системы 
к единственному решению при любом выборе начального приближения, если
а) какая — ни будь из норм матрицы 
б) и только если норма 1 матрицы 
в) и только если норма 1 матрицы 
5. К способам уточнения корней не относится
а) метод проб, метод хорд, метод касательных, метод итераций;
б) метод проб, метод хорд, метод касательных, метод Зейделя;
в) метод проб, метод хорд, метод касательных.
6. Число отрицательных корней уравнения 
а) перемен знака в последовательности коэффициентов 
б) постоянств знака в последовательности коэффициентов 
в) постоянств знака в последовательности коэффициентов 
7. Верхняя граница положительных корней уравнения 
а) 


б) 
в) 

8. Разность между значениями функции в соседних узлах интерполяции называется
а) центральной разностью первого порядка;
б) конечной разностью первого порядка;
в) разделенной разностью первого порядка.
9. Центральные табличные разности используются в интерполяционной формуле
а) Ньютона для равноотстоящих узлов интерполяции;
б) Гаусса для равноотстоящих узлов интерполяции;
в) Эйткина для равноотстоящих узлов интерполяции;
в) Лагранжа для равноотстоящих узлов интерполяции.
10. Квадратурными формулами называются
а) формулы приближенного интегрирования;
б) формула квадратного трехчлена;
в) формулы нахождения квадрата суммы.
11. Операция представления функции 
а) почленным интегрированием;
в) гармоническим анализом.
12. По методу Эйлера 
а) 

б) 
в) 

г) 
д) 

1. Максимальная сумма модулей элементов матрицы по столбцам есть
а) норма 2; б) норма 3; в) норма 1.
2. Норма 3 матрицы 
2. Норма 2 матрицы
а) 38; б) 26; в) 26,4244.
3. Итерационный процесс построения приближений по формуле
а) методом Зейделя; б) методом Ньютона; в) методом итерации.
4. Для оценки погрешности метода Зейделя применяется формула
а)


5. Идея метода хорд состоит в том, что на достаточно малом промежутке 


а)
б) 
в) 
6. Если уравнение полное, то
а) количество его положительных корней равно числу перемен знака
в последовательности коэффициентов или на четное число меньше, а
количество отрицательных корней — числу постоянств знака или на
четное число меньше;
б) количество его положительных корней равно числу постоянств
знака в последовательности коэффициентов или на четное число меньше, а количество отрицательных корней — числу перемен знака или на
четное число меньше;
в) количество его положительных корней равно числу постоянств
знака в последовательности коэффициентов или на четное число меньше.
7. Верхняя граница положительных корней уравнения
по правилу кольца находится по формуле
а) 


б) 
в) 

8. Конечные табличные разности используются в интерполяционной формуле
а) Ньютона; б) Гаусса; в) Эйткина; г) Лагранжа.
9. Разделенные табличные разности используются в интерполяционной формуле
а) Ньютона для равноотстоящих узлов интерполяции;
б) Гаусса для равноотстоящих узлов интерполяции;
в) Ньютона для неравноотстоящих узлов интерполяции;
г) Эйткина для равноотстоящих узлов интерполяции;
д) Лагранжа для неравноотстоящих узлов интерполяции.
10. Формула приближенного вычисления интеграла методом прямоугольников имеет вид
а) 
б) 
в) 
г) 
11. График решения обыкновенного дифференциального уравнения
называется
а) интегральной кривой;
б) кривой второго порядка;
12. По методу Эйлера — Коши приближение решения дифференциального уравнения определяется по формуле
а) 
б) 
в) 

г) 
д) 

1. Корень квадратный из суммы квадратов модулей всех элементов матрицы есть
а) норма 2; б) норма 3; в) норма 1.
2. Норма 2 матрицы 
2. Норма 2 матрицы
а) 38; б) 26; в) 26,4244.
3. Процесс интеграции для системы 
а) больше единицы; б) меньше единицы; в) равно единице.
4. Если для получения значения функции по данному значению аргумента нужно выполнить арифметические операции и возведение в степень с рациональным показателем, то функция называется
а) алгебраической; б) трансцендентной; в) рациональной.
5. Идея метода касательных состоит в том, что на достаточно малом промежутке 


а)
б) 
в) 
6. Число действительных корней уравнения 
а) один положительный корень, два отрицательных корня;
б) два положительных корня, один отрицательный корень;
в) три положительных корня.
7. Основными характеристиками табличных функций являются
а) название функций, объем, шаг, количество знаков табулируемой функции, количество входов;
б) начальное значение, объём, шаг, количество знаков табулируемой функции, количество входов;
в) название функций, объём, шаг, начальное и конечное значения, количество входов.
8. Центральные табличные разности используются в интерполяционной формуле
а) Ньютона; б) Гаусса; в) Эйткина; г) Лагранжа.
9. Интерполяционный многочлен Лагранжа имеет вид:
а) 
б)

в)
10. Формула приближенного вычисления интеграла методом прямоугольников имеет вид
а) 
б) 
в) 
г) 
11. Всякое решение, которое может быть получено из общего при определенных числовых значениях произвольных постоянных, входящих в общее решение, называется
а) допустимым решением дифференциального уравнения;
б) общим решением дифференциального уравнения;
в) частным решением дифференциального уравнения.
12. По методу Эйлера — Коши приближение решения дифференциального уравнения определяется по формуле
а) 
б) 
в) 

г) 
д) 

1. Норма 1 матрицы 
a) 30; 6) 39; в) 28,6356.
2. Норма 1 матрицы 
a) 38; 6) 26; в) 26,4244.
3. Для оценки погрешности метода итерации применяется формула
а)


4. Если для получения значения функции по данному значению
аргумента нужно выполнить арифметические операции и возведение в степень с целым показателем, то функция называется
а) алгебраической; б) трансцендентной; в) рациональной.
5. Идея метода итерации состоит в том, что уравнение
заменяется равносильным ему уравнением 
приближенного значения корня принимается значение, которое
определяется формулой
а)


6. Отделение корней уравнения 
а) 
б) 
в) 
7. Процесс вычисления значений функции в точках 
от узлов интерполяции, называют
8. Разделенные табличные разности используются в интерполяционной формуле
а) Ньютона; б) Гаусса; в) Эйткина; г) Лагранжа.
9. Второй интерполяционный многочлен Ньютона имеет вид:
а) 
б)

в)
10. Квадратурная формула Симпсона имеет вид
а) 
б) 
в) 
г) 
11. Задача отыскания решения дифференциального уравнения,
удовлетворяющего начальным условиям, называется задачей
а) Коши; б) Липшица; в) Пикара.
12. По методу Рунге — Кутта приближенное решение дифференциального уравнения определяется по формуле
а) 
б) 
в) 

г) 
д) 

КЛЮЧИ ПРАВИЛЬНЫХ ОТВЕТОВ
ПО ДИСЦИПЛИНАМ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА», «ЧИСЛЕННЫЕ МЕТОДЫ»
Приближенное вычисление корней в уравнениях
Приближенное вычисление корней в уравнениях
- Приближённое решение уравнений :
1.1 Способ хорд (или способ линейной интерполяции).
- Способ касательных (или способ Ньютона).
- Комбинированный способ (комбинированное применение способов хорд и касательных).
Приближённое решение уравнений.
Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.
В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:
Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.
На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.
Пусть нужно решить уравнение:
Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)
C осью Ох (рисунок №1)
С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.
Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а
Способ хорд (или способ линейной интерполяции).
Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.
Уравнение хорды имеет вид:
Поэтому в точке С:
Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).
Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:
x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)
( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0
Найдём первое приближённое значение корня по формуле (2):
так как f(1,588)=-0,817 0
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.2 Способ касательных (или способ Ньютона).
В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:
и поэтому в точке Д:
Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:
х2` = x1`- f( x1`)/ f`( x1`).
Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:
все более точных приближённых значений корня, причём:
xn+1`= xn`- f(xn`)/ f`( xn`) (8)
Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е
Пример №2. Методом касательных найдём положительный корень уравнения
с точностью до 0,01.
В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:
f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:
x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда
Применяем второй раз способ касательных:
х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;
f(1,643)=0,004, f` (1,643)=15,740;
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.3 Комбинированный способ
(комбинированное применение способов хорд и касательных).
Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:
x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:
Формулы (10) дают:
При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:
При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
http://studyport.ru/referaty/tochnyje-nauki/3800-priblizhennoe-vychislenie-kornej-v-uravnenijah
http://www.bestreferat.ru/referat-284431.html






 Министерство образования и науки РФ
Министерство образования и науки РФ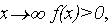 при
при 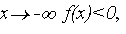 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.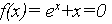 видим, что
видим, что 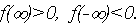 Обнаружив, что
Обнаружив, что 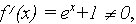 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).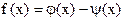 и строить графики функций
и строить графики функций 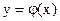 и
и 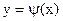 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.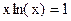 .
.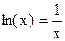 , т.е.
, т.е. 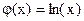 и
и 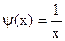 .
.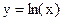 и
и 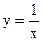 .
.