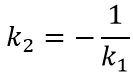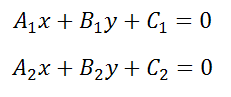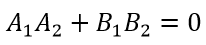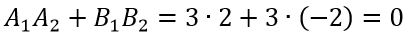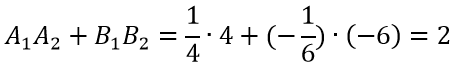Проверить перпендикулярность прямых заданных уравнениями

Перпендикулярные прямые, условие перпендикулярности прямых.

В этой статье подробно рассмотрим перпендикулярные прямые на плоскости и в трехмерном пространстве. Начнем с определения перпендикулярных прямых, покажем обозначения и приведем примеры. После этого приведем необходимое и достаточное условие перпендикулярности двух прямых и детально разберем решения характерных задач.

Навигация по странице.

Перпендикулярные прямые – основные сведения.

Угол между пересекающимися прямыми на плоскости и в трехмерном пространстве может быть равен девяноста градусам. В этом случае говорят, что прямые пересекаются под прямым углом, а прямые называют перпендикулярными. Если угол между скрещивающимися прямыми в трехмерном пространстве равен , то скрещивающиеся прямые также называют перпендикулярными. Таким образом, перпендикулярные прямые на плоскости являются пересекающимися, перпендикулярные прямые в пространстве могут быть как пересекающимися, так и скрещивающимися.

Отметим, что фразы «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» равноправны. Поэтому можно слышать, что перпендикулярные прямые называют взаимно перпендикулярными.

Учитывая все сказанное, дадим общее определение перпендикулярных прямых.

Две прямые называются перпендикулярными, если угол между ними равен .

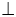
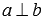
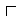
Для обозначения перпендикулярных прямых используют знак перпендикулярности вида «». То есть, если прямые a и b перпендикулярны, то кратко записывают . На чертежах угол между перпендикулярными прямыми отмечают значком прямого угла вида «».

В качестве примера перпендикулярных прямых на плоскости можно привести прямые, на которых лежат стороны квадрата с общей вершиной. В прямоугольной системе координат Oxyz в трехмерном пространстве координатные прямые Ox и Oz , Ox и Oy , Oy и Oz перпендикулярны.

Перпендикулярность прямых — условия перпендикулярности.

Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.

А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?

Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.

Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b .

Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.

Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданы уравнения прямой на плоскости некоторого вида, определяющие прямые a и b . Обозначим направляющие векторы прямых а и b как и соответственно. По уравнениям прямых a и b можно определить координаты направляющих векторов этих прямых – получаем и . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов и , то есть, чтобы скалярное произведение векторов и равнялось нулю: .

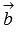
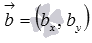
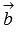
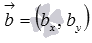
Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид , где и — направляющие векторы прямых a и b соответственно.

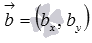
Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.

В прямоугольной системе координат Oxy заданы три точки . Перпендикулярны ли прямые АВ и АС ?

Векторы и являются направляющими векторами прямых АВ и АС . Обратившись к статье координаты вектора по координатам точек его начала и конца, вычисляем . Векторы и перпендикулярны, так как . Таким образом, выполняется необходимое и достаточное условие перпендикулярности прямых АВ и АС . Следовательно, прямые АВ и АС перпендикулярны.

да, прямые перпендикулярны.

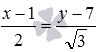
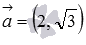
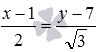
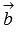
Являются ли прямые и перпендикулярными?

— направляющий вектор прямой , а — направляющий вектор прямой . Вычислим скалярное произведение векторов и : . Оно отлично от нуля, следовательно, направляющие векторы прямых не перпендикулярны. То есть, не выполняется условие перпендикулярности прямых, поэтому, исходные прямые не перпендикулярны.

нет, прямые не перпендикулярны.

Аналогично, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxyz в трехмерном пространстве имеет вид , где и — направляющие векторы прямых a и b соответственно.

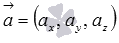
Перпендикулярны ли прямые, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

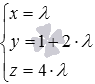
Числа, стоящие в знаменателях канонических уравнений прямой в пространстве, являются соответствующими координатами направляющего вектора прямой. А координатами направляющего вектора прямой, которая задана параметрическими уравнениями прямой в пространстве, являются коэффициенты при параметре. Таким образом, и — направляющие векторы заданных прямых. Выясним, перпендикулярны ли они: . Так как скалярное произведение равно нулю, то эти векторы перпендикулярны. Значит, выполняется условие перпендикулярности заданных прямых.

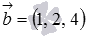
Для проверки перпендикулярности двух прямых на плоскости существуют другие необходимые и достаточные условия перпендикулярности.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы нормальный вектор прямой a был перпендикулярен нормальному вектору прямой b .

Озвученное условие перпендикулярности прямых удобно использовать, если по заданным уравнениям прямых легко находятся координаты нормальных векторов прямых. Этому утверждению отвечает общее уравнение прямой вида , уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом .

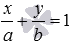
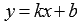
Убедитесь, что прямые и перпендикулярны.

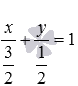
По заданным уравнениям прямых легко найти координаты нормальных векторов этих прямых. – нормальный вектор прямой . Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .

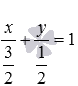
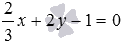
Векторы и перпендикулярны, так как их скалярное произведение равно нулю: . Таким образом, выполняется необходимое и достаточное условие перпендикулярности заданных прямых, то есть, они действительно перпендикулярны.

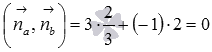
В частности, если прямую a на плоскости определяет уравнение прямой с угловым коэффициентом вида , а прямую b – вида , то нормальные векторы этих прямых имеют координаты и соответственно, а условие перпендикулярности этих прямых сводится к следующему соотношению между угловыми коэффициентами .

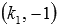
Перпендикулярны ли прямые и ?

Угловой коэффициент прямой равен , а угловой коэффициент прямой равен . Произведение угловых коэффициентов равно минус единице , следовательно, прямые перпендикулярны.

заданные прямые перпендикулярны.

Можно озвучить еще одно условие перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы направляющий вектор одной прямой и нормальный вектор второй прямой были коллинеарны.

Этим условием, очевидно, удобно пользоваться, когда легко находятся координаты направляющего вектора одной прямой и координаты нормального вектора второй прямой, то есть, когда одна прямая задана каноническим уравнением или параметрическими уравнениями прямой на плоскости, а вторая – или общим уравнением прямой, или уравнением прямой в отрезках, или уравнением прямой с угловым коэффициентом.

Являются ли прямые и перпендикулярными?

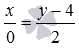
Очевидно, — нормальный вектор прямой , а — направляющий вектор прямой . Векторы и не коллинеарны, так как для них не выполняется условие коллинеарности двух векторов (не существует такого действительного числа t , при котором ). Следовательно, заданные прямые не перпендикулярны.

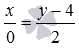
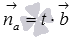
Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Условие перпендикулярности прямых

Условием перпендикулярности (ортогональности) двух прямых на плоскости, заданных уравнениями:

y₁=k₁x+b₁

y₂=k₂x+b₂

или

т.е. угловые коэффициенты k₁ , k₂ обратны по величине и противоположны по знаку и это значит, что прямые перпендикулярны, а если произведение угловых коэффициентов не равно -1, то прямые не перпендикулярны.

Если две прямые представлены следующими уравнениями

то условием их перпендикулярности (уравнение перпендикулярной прямой) есть

Пример 1
Прямые y=4x (прямая синего цвета) и y= -1/4x (прямая красного цвета) перпендикулярны, так как k₁·k₂=4·(-1/4)=-1

Пример 2
Прямые 2x+3y=7 и 3x-2y=4 перпендикулярны, так как A₁=2, A₂=3, B₁=3, B₂=-2, следовательно

Пример 3
Прямые 1/4x-1/6y=0 и 4x-6y=0 не перпендикулярны, так как здесь