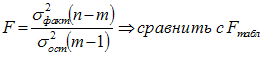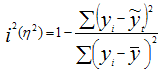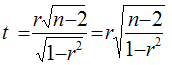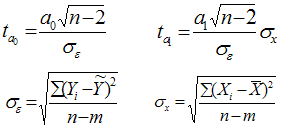Проверка адекватности уравнения регрессии осуществляется с помощью

$ AlexLat $

Оценка значимости уравнения регрессии в целом производится на основе F-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной (y) от среднего значения (y _ср. ) раскладывается на две части – «объясненную» и «необъясненную»:

Схема дисперсионного анализа имеет следующий вид (n –число наблюдений, m–число параметров при переменной x):

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия Фишера. Фактическое значение F -критерия Фишера сравнивается стабличным значением F _табл. (α, k ₁ , k ₂ ) при заданном уровне значимости α и степенях свободы k ₁ = m и k ₂ =n-m-1. При этом, если фактическое значение F-критерия больше табличного F _факт > F _теор , то признается статистическая значимость уравнения в целом. Для парной линейной регрессии m=1 , поэтому:

Эта формула в общем виде может выглядеть так:

Отношение объясненной части дисперсии переменной (у) к общей дисперсии называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи. Соотношение между объясненной и необъясненной частями общей дисперсии можно представить в альтернативном варианте:

Коэффициент детерминации R 2 принимает значения в диапазоне от нуля до единицы 0≤ R 2 ≤1. Коэффициент детерминации R 2 показывает, какая часть дисперсии результативного признака (y) объяснена уравнением регрессии.Чем больше R 2 , тем большая часть дисперсии результативного признака (y) объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между (у) и (x) коэффициент детерминации R 2 будет близок к нулю. Таким образом, коэффициент детерминации R 2 может применяться для оценки качества (точности) уравнения регрессии. Возникает вопрос, при каких значениях R 2 уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использование в анализе? Ответ на этот вопрос дает F — критерий Фишера F _факт > F _теор — делаем вывод о статистической значимости уравнения регрессии. Величина F — критерия связана с коэффициентом детерминации R 2 _xy ( r 2 _xy ), и ее можно рассчитать по следующей формуле:

Либо при оценке значимости индекса (аналог коэффициента) детерминации:

где: i 2 — индекс (коэффициент) детерминации, который рассчитывается:

Использование коэффициента множественной детерминации R 2 для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину R 2 . Поэтому, при большом количестве факторов, предпочтительнее использовать, так называемый, улучшенный, скорректированный коэффициент множественной детерминации R 2 , определяемый соотношением:

где p – число факторов в уравнении регрессии, n – число наблюдений. Чем больше величина p, тем сильнее различия между множественным коэффициентом детерминации R 2 и скорректированным R 2 . При использовании скорректированного R 2 , для оценки целесообразности включения фактора в уравнение регрессии, следует учитывать, что увеличение его величины (значения), при включении нового фактора, не обязательно свидетельствует о его значимости, так как значение увеличивается всегда, когда t-статистика больше единицы (|t|>1). При заданном объеме наблюдений и при прочих равных условиях, с увеличением числа независимых переменных (параметров), скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений, скорректированная величина коэффициента множественной детерминации R 2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель. Низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации R 2 может быть обусловлено следующими причинами: в регрессионную модель не включены существенные факторы; неверно выбрана форма аналитической зависимости, не реально отражающая соотношения между переменными, включенными в модель.

Для оценки значимости парного коэффициента корреляции (корень квадратный из коэффициента детерминации), при условии линейной формы связи между факторами, можно использовать t-критерий Стьюдента:

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия для параметров a 0 а 1 :

n-число наблюдений, m-число параметров уравнения регрессии, σ _ε -(остаточное) среднее квадратическое отклонение результативного признака от выровненных значений ŷ; σ _х -среднее квадратическое отклонение факторного признака от общей средней.

Вычисленные, по вышеприведенным формулам, значения сравнивают с критическими t, которые определяют по таблице значений Стьюдента с учетом принятого уровня значимости α и числа степеней свободы вариации k (ν)=n-2. В социально-экономических исследованиях уровень значимости α обычно принимают равным 0,05. Параметр признаётся значимым (существенным) при условии, если t _расч. > t _табл. В этом случае, практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.

Проверка адекватности линейного уравнения регрессии

Расчет коэффициентов ПФЭ при равном числе параллельных опытов в каждой точке факторного пространства

Коэффициенты находятся по формуле:

,

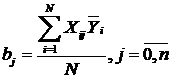
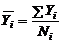
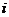
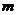
где — среднее значение параметра оптимизации, вычисленное по параллельным опытам – ой строки матрицы планирования .

Проверка значимости коэффициентов ПФЭ

Очевидно, что один фактор больше влияет на параметр оптимизации, другой – меньше. Поэтому можно проверить полученные коэффициенты регрессии на значимость, т.е. оценить величину влияния каждого фактора на значение параметра оптимизации. Если эта величина соизмерима с ошибкой эксперимента, то соответствующий коэффициент не несет дополнительной информации об объекте, и его можно приравнять к нулю, что упрощает математическую модель.

Значимость коэффициентов проверяется с помощью 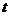– критерия Стьюдента.

Значения 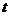– критерия вычисляются для каждого для каждого фактора по формуле:

,

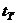
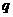
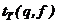
Полученные значения сравнивают с табличным значением критерия Стъюдента , которое находится по числу степеней свободы , и уровню значимости α — величина, характеризующая вероятность того, что решение будет неправильным. Обычно принимают, что α =0.05.

> ,

то коэффициент значимо отличается от нуля, если же , (1)

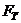
то линейное уравнение регрессии признается адекватным. Если это условие не выполняется, т.е.

При расчете F предполагается что 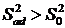. Если наблюдается обратное, то вывод об адекватности может быть сделан и без проверки условия (1).

Если модель адекватна, то ее можно использовать для поиска области оптимума объекта исследования или для предсказания отклика.

При неадекватной линейной модели наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента.

Итак, алгоритм расчета линейной модели с использованием ПФЭ следующий:

Задают матрицу планирования в кодированной форме для заданного числа факторов

Для каждого фактора задают базовую точку и интервал варьирования

Рассчитывают матрицу планирования в натуральной (размерной) форме

Проводят эксперименты, по матрице планирования, используя случайные числа.

Проводят серию опытов в центре плана, для определения ошибки опыта.

Электронная библиотека

Совокупность действий, связанных с составлением уравнения регрессии, называется регрессионным анализом. Регрессионный анализ результатов однофакторного эксперимента включает в себя следующие действия:

1) подбор вида уравнения регрессии. Осуществляется с помощью, например, функциональных шкал;

2) определение постоянных коэффициентов в уравнении регрессии. Осуществляется с помощью МНК;

3) проверку соответствия (адекватности) уравнения регрессии результатам опытов.

Проверка адекватности уравнения регрессии результатам опытов проводится следующим образом:

1) По результатам повторных изменений в каждом опыте вычисляются дисперсия функции отклика (σ_у 2 ), среднеквадратичная погрешность ( ), доверительный интервал 9 ), математическое ожидание ( ).

2) Осуществляется проверка однородности дисперсии , где j = 1,2,…, N – число опытов. Дисперсии называются однородными, если при неограниченном увеличении числа повторных измерений п в каждом из опытов они стремятся к общему пределу, т.е.

Дисперсии проверяются на однородность с помощью критериев Фишера, Кохрена, Бартлета. Наиболее просто осуществить проверку однородности с помощью критерия Фишера. Для этого из всех дисперсий ( ) выбирают две: наибольшую ( ) и наименьшую ( ).

Отношение / сравнивают с табличным значением критерия Фишера (F):

· если / F – дисперсии неоднородны.

Значения критерия Фишера берутся из таблицы 2.3, составленной при доверительной вероятности Р = 0,95, для числа степеней свободы числителя (дисперсии ) и числа степеней свободы знаменателя (дисперсии ).

Если в каждом из опытов число повторных измерений одинаково и равно п, то f_числ = f_знам = п – 1.

Если дисперсии и неоднородны, то это означает, что число повторных измерений недостаточно или что среди результатов повторных измерений опыта с дисперсией находится промах.

Следует очистить результаты повторных измерений от промахов, увеличить число повторных измерений, снова определить и проверить их однородность. Если все дисперсии и однородны, можно переходить к следующему действию.

3) Вычисляется дисперсия воспроизводимости (S 2 _воспр). Дисперсия воспроизводимости – это среднее из дисперсий ( ) всех опытов. Дисперсия воспроизводимости характеризует средний разброс результатов повторных измерений во всех опытах относительно своих математических ожиданий.

Если в каждом опыте число повторных измерений одинаково и равно п, то S 2 _воспр определяется по формуле:

где N – число опытов, – математическое ожидание в j-м опыте. Если в опытах число повторных измерений различно, то S 2 _воспр определяется как средневзвешенная величина

где — число повторных измерений в j—м опыте.

Число степеней свободы дисперсии воспроизводимости равно сумме чисел степеней свободы дисперсий опытов:

4) Вычисляется дисперсия адекватности (S 2 _ад). Дисперсия адекватности – это сумма квадратов отклонений расчётных и экспериментальных значений функции отклика в каждом опыте, отнесённая к числу степеней свободы. Она характеризует разброс экспериментальных результатов относительно расчётных и определяется по формуле:

где т – число постоянных коэффициентов в уравнении регрессии; — математическое ожидание в j—м опыте; N – m = f_ад – число степеней свободы дисперсии адекватности;

3) Проверяется однородность дисперсий адекватности и воспроизводимости. Дисперсии адекватности и воспроизводимости будут однородными, если их отношение будет меньше табличного значения критерия Фишера:

S 2 _ад / S 2 _воспр 2 _ад и S 2 _воспр однородны , то с доверительной вероятностью Р = 0,95 можно утверждать, что составленное уравнение регрессии адекватно. Это следует из того, что при и разброс экспериментальных значений функции отклика относительно её расчётных значений равен среднему разбросу результатов повторных измерений в каждом опыте относительно своих математических ожиданий.

Если S 2 _ад / S 2 _воспр > F, то выбранное уравнение регрессии неадекватно. Следует перейти к уравнению регрессии более высокого порядка или выбрать уравнение регрессии другого вида, определить значения коэффициента и снова проверить адекватность.

Если опыты состоят из однократных измерений, то адекватность уравнения регрессии не может быть проверена изложенным способом. В этом случае проверка адекватности уравнения регрессии может быть осуществлена сравнением доверительного интервала функции отклика (а_у) с отклонениями расчётных и экспериментальных значений функции отклика ( ). Очевидно, что, если Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00