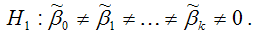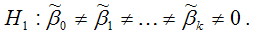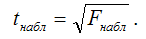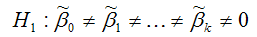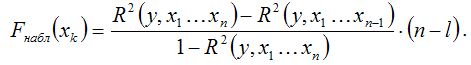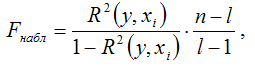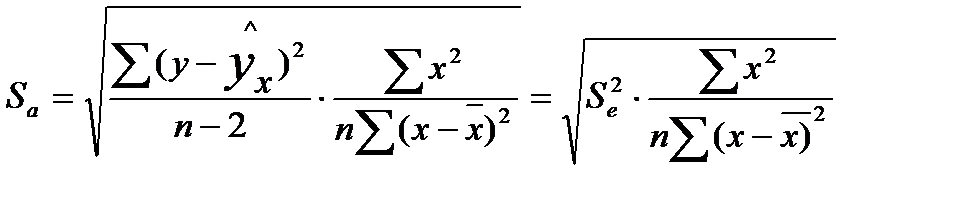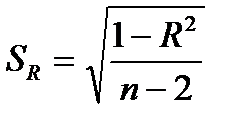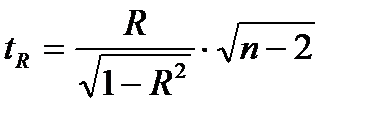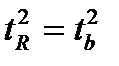Использование критерия Стьюдента для проверки значимости параметров регрессионной модели
Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:
где P — значение параметра;
Sp — стандартное отклонение параметра.
Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N—k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).
Если вычисленное значение tp выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.
Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.
Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.
Основная гипотеза состоит в предположении о незначимости коэффициентов модели множественной регрессии, т. е.
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов модели множественной регрессии, т. е.
Данные гипотезы проверяются с помощью t-критерия Стьюдента, который вычисляется посредством частного F-критерия Фишера-Снедекора.
При проверке основной гипотезы о значимости коэффициентов модели множественной регрессии применяется зависимость, которая существует между t-критерием Стьюдента и частным F-критерием Фишера-Снедекора:
При проверке значимости коэффициентов модели множественной регрессии критическое значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида
наблюдаемое значение частного F-критерия Фишера-Снедекора рассчитывается по формуле:
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение t-критерия больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
tнабл≥tкрит, то основная гипотеза о незначимости коэффициента βk модели множественной регрессии отвергается, и он является значимым.
Если наблюдаемое значение t-критерия меньше критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. tнабл , то основная гипотеза о незначимости коэффициента βk модели множественной регрессии принимается.
Проверка основной гипотезы о значимости модели множественной регрессии в целом состоит в проверке гипотезы о значимости коэффициента множественной корреляции или значимости параметров модели регрессии.
Если проверка значимости модели множественной регрессии в целом осуществляется через проверку гипотезы о значимости коэффициента множественно корреляции, то выдвигается основная гипотеза вида Н0:R(y,xi)=0, утверждающая, что коэффициент множественной корреляции является незначимым, и, следовательно, модель множественной регрессии в целом также является незначимой.
Обратная или конкурирующая гипотеза вида Н1:R(y,xi)≠0 утверждает, что коэффициент множественной корреляции является значимым, и, следовательно, модель множественной регрессии в целом также является значимой.
Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.
Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим.
При проверке значимости коэффициента множественной корреляции критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l–1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.
При проверке основной гипотезы вида Н0:R(y,xi наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:
где R 2 (y,xi) – коэффициент множественный детерминации.
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл>Fкрит, то с вероятностью а основная гипотеза о незначимости коэффициента множественной корреляции отвергается, и он признаётся значимым. Следовательно, модель множественной регрессии в целом также является значимой.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т.е. Fнабл≤Fкрит, то основная гипотеза о незначимости коэффициента множественной корреляции принимается, и он признаётся незначимым. В этом случае модель множественной регрессии признаётся незначимой.
Проверка на статистическую значимость коэффициентов уравнения регрессии и корреляции.
Качество подбора функции регрессии можно оценить с помощью стандартных ошибок или оценок параметров регрессии. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартного отклонения, т.е.:
Стандартные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
где 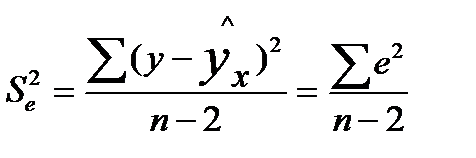
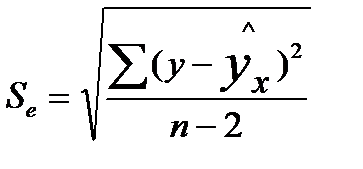
Сравнивая фактическое (расчетное) и критическое (табличное) значения t-статистики, т.е. tфакт и tкрит = t n-1;α — отвергаем или не отвергаем гипотезу Н0:
—если tкрит tфакт,то Н0 не отклоняется и признается случайная природа формирования a, b и R..
Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует, что в парной регрессии 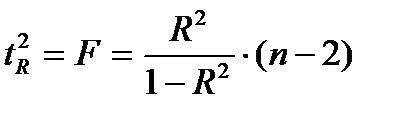
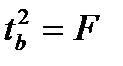
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
Формулы для расчета доверительных интервалов a, b имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, т.к. он не может одновременно принимать и положительное, и отрицательное значения.
8.Проверка общего качества уравнения регрессии. Для оценки качества построенной модели используют коэффициент (индекс) детерминации — R 2 , а также среднюю ошибку аппроксимации — А.
F-тест — оценивание качества уравнения регрессии – состоит в проверке гипотезы H0 о статистической не значимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fтабл определяется из соотношения значения объясненной и остаточной дисперсии, рассчитанных на одну степень свободы:
где n — объем выборки (объем статистической информации).
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a — вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.
Если Fтабл Fфакт, то гипотеза H0 не отклоняется и признаётся статистическая незначимость, ненадёжность уравнения регрессии.
9.Интервалы прогноза по линейному уравнению регрессии.В прогнозных расчетах по уравнению регрессии определяется предсказываемое (расчетное) упрог значение как точечный прогноз 
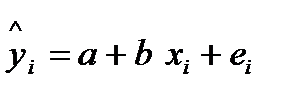



S 
Средняя стандартная ошибка прогноза Sпрогноз вычисляется по формуле:

а доверительный интервал прогноза строится по формуле:
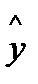

При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора.
10.Таблица дисперсионного анализа. Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:å 


где 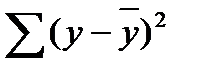
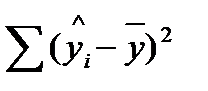
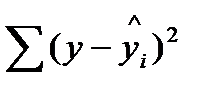
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Дисперсия на одну степень свободы |
| Общая | 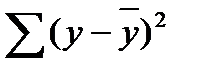 | n-1 | — |
| Факторная | 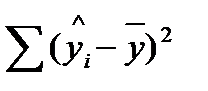 | m | 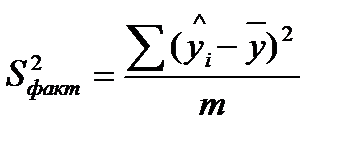 |
| Остаточная | 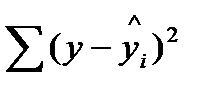 | n-m-1 |  |
Нелинейная регрессия
Нелинейная регрессия -частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако в силу однообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравнениями регрессии, безусловно, не даст положительного результата. Например, при рассмотрении спроса Y на некоторый товар от цены X данного товара в ряде случаев можно ограничиться линейным уравнением регрессии: Y=β0+β1X . Здесь β1 характеризует абсолютное изменение Y (в среднем) при единичном изменении X. Если же мы хотим проанализировать эластичность спроса по цене, то приведенное уравнение не позволит это осуществить. В этом случае целесообразно рассмотреть так называемую логарифмическую модель
При анализе издержек Y от объема выпуска X наиболее обоснованной является полиноминальная (точнее, кубическая) модель При рассмотрении производственных функций линейная модель является нереалистичной. В этом случае обычно используются степенные модели. Например, широкую известность имеет производственная функция Кобба-Дугласа Y=AK α L β (здесь Y – объем выпуска; K и L – затраты капитала и труда соответственно; A, α и β – параметры модели).
Достаточно широко применяются в современном эконометрическом анализе и многие другие модели, в частности обратная и экспоненциальная модели.
Построение и анализ нелинейных моделей имеют свою специфику. Приведенные выше примеры и рассуждения дают основания более детально рассмотреть возможные нелинейные модели.
http://be5.biz/ekonomika/e008/35.html
http://poisk-ru.ru/s51764t1.html