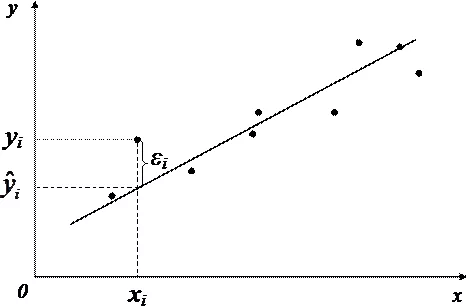
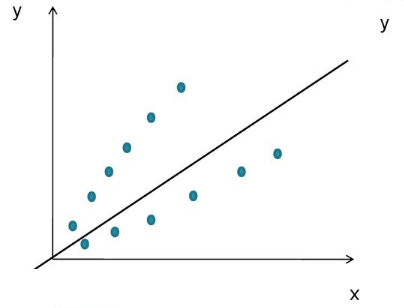
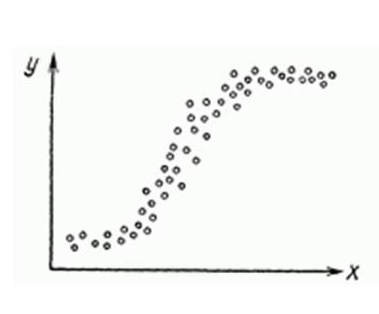
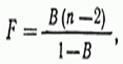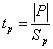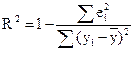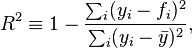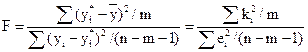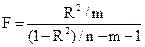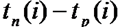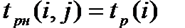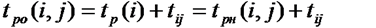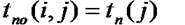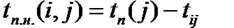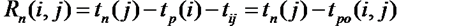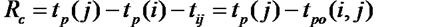Проверка значимости уравнения регрессии коэффициент детерминации

Пример нахождения статистической значимости коэффициентов регрессии

Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
,
где — оценка параметра регрессии, полученная по наблюдаемым данным;
μ_a – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
, где r_yx — оценка коэффициента корреляции, полученная по наблюдаемым данным; m_r – стандартная ошибка коэффициента корреляции r_yx.
Для линейного парного уравнения регрессии:
.
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ₍ _b ₌₀₎ = t ₍_r₌₀₎.

Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
69	124	4761	15376	8556	128.48	491.36	20.11	367.36
83	133	6889	17689	11039	141.4	173.36	70.56	26.69
92	146	8464	21316	13432	149.7	0.03	13.71	14.69
97	153	9409	23409	14841	154.32	46.69	1.73	78.03
88	138	7744	19044	12144	146.01	66.69	64.21	0.03
93	159	8649	25281	14787	150.63	164.69	70.13	23.36
74	145	5476	21025	10730	133.1	1.36	141.68	200.69
79	152	6241	23104	12008	137.71	34.03	204.21	84.03
105	168	11025	28224	17640	161.7	476.69	39.74	283.36
99	154	9801	23716	15246	156.16	61.36	4.67	117.36
85	127	7225	16129	10795	143.25	367.36	263.91	10.03
94	155	8836	24025	14570	151.55	78.03	11.91	34.03
1058	1754	94520	258338	155788	1754	1961.67	906.57	1239.67

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S _a = 0.2704
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).

Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.812):
(a — t_табл·S _a; a + t_табл·S_a)
(0.4325;1.4126)
(b — t_табл·S _b; b + t_табл·S_b)
(21.3389;108.3164)
2) F-статистики

Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.

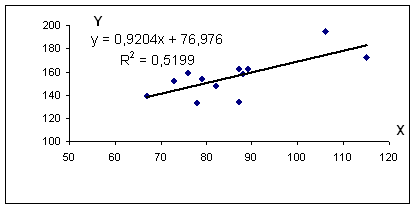
Пример №2 . По территориям региона приводятся данные за 199Х г.;

Среднедневная заработная плата, руб., у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Решение находим с помощью калькулятора.
Использование графического метода .
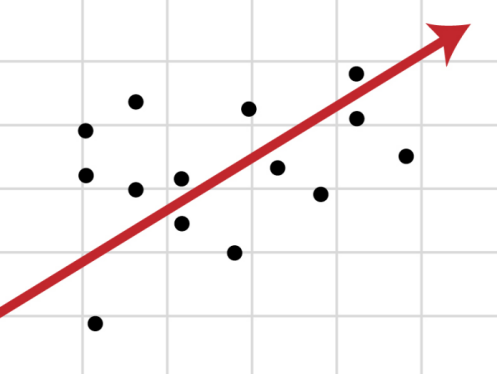
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.

Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.

y 2	x·y	y(x)	(y i — y ) 2	(y-y(x)) 2	(x i — x ) 2	\|y-y x \|:y
78	133	6084	17689	10374	148,77	517,56	248,7	57,51	0,1186
82	148	6724	21904	12136	152,45	60,06	19,82	12,84	0,0301
87	134	7569	17956	11658	157,05	473,06	531,48	2,01	0,172
79	154	6241	23716	12166	149,69	3,06	18,57	43,34	0,028
89	162	7921	26244	14418	158,89	39,06	9,64	11,67	0,0192
106	195	11236	38025	20670	174,54	1540,56	418,52	416,84	0,1049
67	139	4489	19321	9313	138,65	280,56	0,1258	345,34	0,0026
88	158	7744	24964	13904	157,97	5,06	0,0007	5,84	0,0002
73	152	5329	23104	11096	144,17	14,06	61,34	158,34	0,0515
87	162	7569	26244	14094	157,05	39,06	24,46	2,01	0,0305
76	159	5776	25281	12084	146,93	10,56	145,7	91,84	0,0759
115	173	13225	29929	19895	182,83	297,56	96,55	865,34	0,0568
1027	1869	89907	294377	161808	1869	3280,25	1574,92	2012,92	0,6902

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим t_крит:
t_крит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bx_p ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 94

(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (10;0.05) = 1.812

Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-t_a)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Проверка значимости коэффициента детерминации.

При выполнении процедуры проверки значимости коэффициента детерминации выдвигается нулевая гипотеза Нo против альтернативной H1 которые заключаются в следующем:

Нo: существенного различия между выборочным коэффициентом детерминации и коэффициентом детерминации генеральной совокупности B(r) = 0 нет.

Эта гипотеза равносильна гипотезе Нo : β1 = β2 = … = βm = 0, т. е. ни одна из объясняющих переменных, включенных в регрессию, не оказывает существенного влияния на зависимую переменную.

Н1: выборочный коэффициент детерминации существенно больше коэффициента детерминации генеральной совокупности В(г) = 0.

Из постановки задачи ясно, что следует использовать одностороннюю критическую область. Принятие гипотезы Н1 означает, что по крайней мере одна из m объясняющих переменных, включенных в регрессию, оказывает существенное влияние на переменную у.

Для оценки значимости парного коэффициента детерминации используется статистика

Имеющая F-распределение Фишера с f1 = m = 1 и f2 = n – 2 степенями свободы. Значение статистики, вычисленное вышеприведенной формуле, сравнивается с критическим значением этой статистики при заданном уровне значимости £ и соответствующем числе степеней свободы. Если F > Ff1; f2;£, то вычисленный коэффициент детерминации значимо отличается от нуля. Этот вывод обеспечивается с вероятностью 1 — £.

28 Проверка значимости коэффициентов регрессии

Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:

где P — значение параметра;
S_p — стандартное отклонение параметра.

Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N—k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной моделиY=A*X+B подставляем k=1).

Если вычисленное значение t_p выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.

Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.

29 Проверка общего качества уравнения регрессии. Коэффициент детерминации. Проверка значимости коэффициента детерминации

После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии. Для этой цели, как и в случае парной регрессии, используется коэффициент детерминации R 2 , который рассчитывается по формуле:

В общем случае 0 2 2 .

Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R . Действительно, каждая следующая объясняющая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. Это уменьшает (в худшем случае не увеличивает) область неопределенности в поведении Y.

Коэффициент детерминации ( 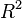)— это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.

Формула для вычисления коэффициента детерминации:

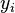
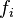
где — выборочные данные, а — соответствующие им значения модели.

Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.

Коэффициент принимает значения из интервала 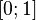. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть .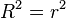

После оценки индивидуальной статистической значимости каждого из коэффициентов регрессии обычно анализируется совокупная значимость коэффициентов. Такой анализ осуществляется на основе проверки гипотезы об общей значимости — гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех m объясняющих переменных X₁, Х₂, . Х_m модели на зависимую переменную Y можно считать статистически несущественным, а общее качество уравнения регрессии невысоким.

Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий.

H₀: (объясненная дисперсия) = (остаточная дисперсия),

H₁: (объясненная дисперсия) > (остаточная дисперсия).

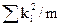
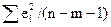
где — объясненная дисперсия; — остаточная дисперсия. При выполнении предпосылок МНК построенная F-статистика имеет распределение Фишера с числами степеней свободы ν₁=m, ν₂= n-m-1. Поэтому, если при требуемом уровне значимости α F_набл > F_α,m,n-m-1= F_кр (критическая точка распределения Фишера), то H₀отклоняется в пользу H₁. Это означает, что объясненная дисперсия существенно больше остаточной дисперсии, а следовательно, уравнение регрессии достаточно качественно отражает динамику изменения зависимой переменной Y.

Однако на практике чаще вместо указанной гипотезы проверяют тесно связанную с ней гипотезу о статистической значимости коэффициента детерминации R 2 :

Для проверки данной гипотезы используется следующая F-статистика:

Величина F при выполнении предпосылок МНК и при справедливости. Но имеет распределение Фишера, аналогичное распределению F-статистики.

Анализ статистики F позволяет сделать вывод о том, что для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детерминации R 2 не должен существенно отличаться от нуля. Его критическое значение уменьшается при росте числа наблюдений и может стать сколь угодно малым.

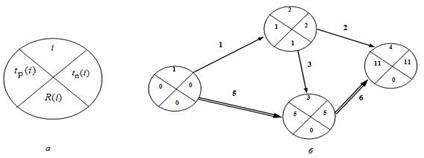
30. Путь, полный путь, критический путь, определение критического пути четырехсекторным методом.

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующий за ней работы.

Полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.

Критич. путь — полный путь, имеющий наибольшую длину (продолжительность) из всех полных путей. Eгo длина опред. срок выполнения работ по сетевому графику. В rрафике может быть несколько критич. путей. Работы, лежащие на критич. пути, наз. критическими. Увеличение продолжительности критич. работ соответств. увеличивает общую продолжительность работ по СГ.

При четырехсекторном способе определения критического пути кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис.а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события tp(i), в правом – наиболее позднее из допустимых время свершения события tп(i), в нижнем – резерв времени данного события R(i).

Рисунок: а) обозначения в вершине графика; б) сетевой график.

Раннее время свершения события tp(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: tp(i)=max(t) до (i).

Послойно, переходя от исходного события до конечного, определим tp(i). Всегда для начального события tp(1)=0.

Для события 3 (рис., б) – tp(3)=max<1+3,0+5>=5; для события 4 – tp(4)=max<1+2,5+6>=11.

Длина критического пути Lкр=11. Послойно, переходя от конечного события до начального, определим tп(i). Всегда для конечного события tп(4)=t(Lкр)=11. Позднее время свершения события tп(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(Lкр), можно найти tп(i)= t(Lкр)-max(t) после (i).

Для события 2 – tп(3)=11-max<3+6,2>=2.

Для критического пути время раннего свершения события tp(i) равно времени позднего свершения этого события tп(i), т.е. tp(i)= tп(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= tп(i)- tp(i).

Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.

Связь параметров сетевого графика для событий и работ показана в таблице.

Таблица — Расчет параметров работ

Время	Начало i → j Окончание
Раннее	t_рн(ij)= t_p(i)	t_ро(ij)= t_p(i)+t_ij
Позднее	t_пн(ij)= t_п(j)-t_ij	t_по(ij)= t_п(j)

Резерв времени для работы R(ij) определяется по формуле: R(ij)= tп(j)- tр(i)-tij.

31. Расчет временных параметров событий в задачах сетевого планирования.

При анализе сетевого графика прежде всего вычисляют его временные параметры. К основным временным параметрам относятся:

— продолжительность критического пути (критический срок);

— сроки свершения и резервы сетей;

— сроки выполнения отдельных работ и их резервы времени.

Основные временные параметры

Элемент сети	Наименование параметра	условное обозначение
Событии,i	Ранний срок свершения события	t_p(i)
Поздний срок свершения события	t_n(i)
Резерв времени события	R(i)
Работа i,j	Продолжительность работы	t_ij

Ранний срок свершения событий – самый ранний момент, в котором завершаются все работы предшествующие этому событию. Рассчитывается по формуле:

,где — ранний срок свершения события i.

— продолжительность работы i, j.

— подмножество, включающее все работы входящие в событие j.

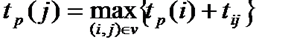
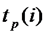
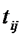
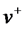
Поздний срок свершения события – такой предельный момент, после которого остаётся столько времени, сколько необходимо для выполнения всех работ следующих за этим событием.

Рассчитывается по формуле: .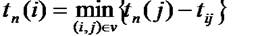

Резерв времени события показывает, на какой предельно допустимый срок может задержаться свершение событий i без нарушения сроков наступления завершающего события.

R(i)=

Резервы времени критических событий=0

Ранний срок начала работы совпадает с ранним сроком свершения событий i.

Ранний срок окончания работы определяется по формуле:

Поздний срок окончания работы совпадает с поздним сроком свершения события j.

Поздний срок начала работы определяется по формуле:

Полный резерв времени работы — это максимальный запас времени, на которое можно задержать начало работы или увеличить её продолжительность при условии, что весь комплекс работ будет завершён в критический срок.

Свободный резерв времени работы — это максимальный запас времени, на который можно отсрочить или увеличить её продолжительность при условии, что не нарушаться ранние сроки начала всех последующих работ.

Критические работы, как и критические события резервов не имеют.

Расчёт временных параметров сетевой модели проводят в 4 этапа:

1) прямой – вычисления начинаются с исходного события и продолжаются пока не будет достигнуто завершающее событие. Для каждого события вычисляется ранний срок его свершения.

2) обратный – вычисление начинается с обратного события и продолжается пока не будет достигнуто исходное событие. Для каждого события рассчитывается поздний срок его свершения.

3) вычисляются резервы времени событий и выделяется критический путь. Критический путь – это самый продолжительный путь, который проходит через события, резерв времени которых равен нулю.

4) строится сводная таблица временных параметров события.

32. Регрессии. Нелинейные по переменным и их построение.

Чтобы написать ту или иную зависимость прим. ур-ие регрессии – ур-ие, связыв. между собой фактор признаки и результативные признаки. Ур-ие регрессии бывают линейные и нелинейные. Сама регрессия бывает парная (зав-сть между 1-им фактор признаком и результатом) y = y(x) ; и множественнаяy = a + bx (парная линейная регрессия, т.к. х и у участвуют в 1-ой степени, а и b – параметры рег. имеющие эк. смысл).При иссл. соц.-экон. явл. и процессов далеко не все зависимости можно описать с помощью лин. связи. Т.О. в ЭММ широко использ. класс нелин. моделей регрессии, кот. делятся на 2 класса:1) модели регрессии, нелин. относительно включенных в анализ независ. переменных, но линейные по оцениваемым параметрам;2) модели регрессии, нелинейные по оцениваемым параметрам.Для оценки параметров нелинейных моделей используют два подхода. 1.основан на линеаризации модели (с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линей. соотношения между преобразованными переменными). 2.применяют в случаях, когда подобрать соответствующее линеаризующее преобразование не удается. Тогда исп. методы нелин. оптимизации на основе исходных переменных. Оценка параметров регрессии, нелинейной по переменным, включенным в анализ, но линейной по оцениваемым параметрам, проводится с помощью МНК путем решения системы линейных алгебр.уравнений. К моделям регрессии, нелинейным относительно включённых в анализ независимых переменных (но линейных по оцениваемым параметрам), относятся полиномы выше второго порядка и гиперболическая функция. Эти модели представляют собой что зависимая переменная yi линейно связана с параметрами модели.Полиномы или полин. функции примен. при анализе процессов с монотонным развитием и отсутствием пределов роста. (нап.натур.показатели пром. про-ва). Полин. функции характер. 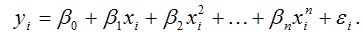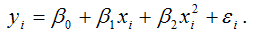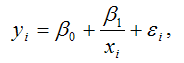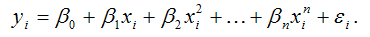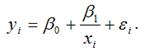отсутствием явной зависимости приростов факторных переменных от значений результативной переменной yi.Общий вид полинома n-го порядка (n-ой степени): Чаще всего в ЭММ примен. полином второго порядка (параболическая функция), характ. равноускоренное развитие процесса (равноускоренный рост или снижение уровней).: Гиперболическая функция характеризует нелин. зависимость между результативной переменной yi и факторной переменной xi, однако, эта функция является лин.по оцениваемым параметрам.( модель зависимости затрат на единицу продукции от объёма производства)Гиперболоид или гиперболическая функция имеет вид: Данная гиперб. функция является равносторонней.Неизвестные параметры модели регрессии, нелинейной по факторным переменным, можно найти только после того, как модели будет приведена к линейному виду.Для того чтобы оценить неизвестные параметры нелин. регрессионной модели необходимо привести её к линейному виду. Суть процесс линеаризации нелин. по факторным переменным моделей регрессии заключается в замене нелин. факторных переменных на лин. переменные.Рассмотрим процесс линеаризации полиномиальной функции порядка n: Заменим все факторные переменные на линейные следующим образом:x=c1; x2=c2; x3=c3; … xn=cn.Тогда модель множественной регрессии можно записать в виде:yi= Рассмотрим процесс линеаризации гиперболической функции: Данная функция может быть приведена к линейному виду путём замены нелин.факторной переменной 1/x на лин.переменную с. Тогда модель регрессии можно записать в виде:yi=Следовательно, модели регрессии, нелин. относительно включенных в анализ независимых переменных, но лин. по оцениваемым параметрам, могут быть преобразованы к лин. виду. Это позволяет применять к линеаризованным моделям регрессии классические методы определения неизвестных параметров модели (метод наименьших квадратов ), а также методы проверки различных гипотез.33. Резервы времени работ в задачах сетевого планирования Путь характеризуется двумя показателями — продолжительностью и резервом. Для событий рассчитывают три характеристики: ранний и поздний срок совершения события, а также его резерв.
Ранний срок свершения события определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события, причем tр(1)=0, a tр(N)=tKp(L):
tр(j)=max; j=2,…,N
Поздний срок свершения события характеризует самый поздний допустимый срок, к которому должно совершиться событие, не вызывая при этом срыва срока свершения конечного события:
tn(i)=min; j=2,…,N-1
Этот показатель определяется «обратным ходом», начиная с завершающего события, с учетом соотношения tn(N)=tp(N).
Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i):
R(i)=tn(i)-tp(i)
Резерв определяется как разность между длинами критического и рассматриваемого путей. Из этого определения следует, что работы, лежащие на критическом пути, и сам критический путь имеют нулевой резерв времени. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности общего срока выполнения всех работ.Резерв показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ. Для всех работ (i,j) на основе ранних и поздних сроков свершения всех событий можно определить показатели:
Ранний срок начала— tpn(i,j)=p(i) ;
Ранний срок окончания — tpo(i,j)=tp(i)+t(i,j);
Поздний срок окончания — tno(U)=tn(j);
Поздний срок начала —tпн(i,j)=tn(j)-t(i,j);
Полный резерв времени —Rn(i,j)=tn(j)-tp(i)-t(i,j);
Независимый резерв —
Rн(i,j)=max<0; tp(j)–tn(i)-t(i,j)>=max<0;Rn(i,j)-R(i)-R(j)>.
Полный резерв времени показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится.
Независимый резерв времени соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие — начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.

34. Сроки раннего и позднего начала и окончания работ в задачах сетевого планирования

Работа – это некоторый процесс, приводящий к достижению определенного результата и требующий затрат каких-либо ресурсов, имеет протяженность во времени.

Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями

– ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i

– поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;

– резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.

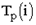
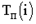
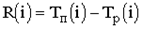
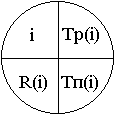Временные параметры работ определяются на основе ранних и поздних сроков событий:

· – ранний срок начала работы;

· – ранний срок окончания работы;

· – поздний срок окончания работы;

· – поздний срок начала работы;

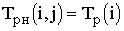
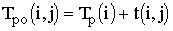
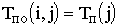
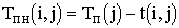
35. Сроки совершения событий в задачах сетевого планирования

Событие – момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и, в отличие от работ, не имеет протяженности во времени. Например, фундамент залит бетоном, комплектующие поставлены, отчеты сданы.

В сетевой модели имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.

Путь – это последовательность работ в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Полный путь – это путь от исходного до завершающего события. Критический путь –максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими. Критические работы имеют нулевые свободные и полные резервы. Подкритический путь – полный путь, ближайший по длительности к критическому пути. Сетевой график может содержать не один, а несколько критических путей. Критическими называются также работы и события, расположенные на этом пути. Резервный интервал от t до t* для событий, лежащих на критическом пути, равен 0. Для завершающего события сетевого графика поздний срок свершения события должен равняться его раннему сроку, т. е. tп = t*п.

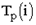
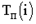
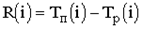
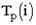
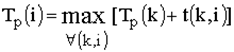
Ранние сроки свершения событий рассчитываются от исходного (И) к завершающему (З) событию следующим образом:

1) для исходного события И ;

2) для всех остальных событий I

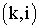
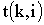
где максимум берется по всем работам , входящим в событие i; – длительность работы (k,i)

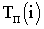
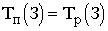
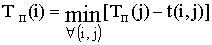
Поздние сроки свершения событий рассчитываются от завершающего к исходному событию:

1) для завершающего события З ;

2) для всех остальных событий

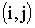
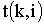
где минимум берется по всем работам , выходящим из события i; – длительность работы (k,i)

36. Схема межотраслевого баланса за отчетный период в стоимостном выражении

Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, хар-щая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевые балансы могут разрабатываться на плановый и отчетный период в натуральном, натурально-стоимостном и стоимостном выражении.

МОБ в натуральном выражении (в физических измерителях) охватывают только важнейшие виды продукции. Натурально-стоимостной (баланс смешанного типа) охватывает весь общественный продукт. Стоимостной баланс характеризует процесс воспроизводства в денежном выражении.

МОБ представлен в виде системы линейных уравнений. МОБ представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостной состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.

В. Леонтьев создал научно обоснованный метод «затраты-выпуск», который позволяет анализировать межотраслевые связи в национальном хозяйстве и определять возможные направления оптимизации отраслевой структуры.

В общем виде модель МОБ Леонтьева имеет следующий вид:

где X- объем производства какой-либо отрасли;Y — конечный продукт этой отрасли;А — матрица технологических коэффициентов прямых затрат, aij, которые показывают, сколько продукции отрасли необходимо затратить для производства единицы продукции отрасли.

37. Типы данных и виды переменных в эконометрических задачах

При эконометрическом моделировании экономических процессов используют следующие типы эмпирических (статистических) данных:

Пространственными данными является набор сведений по разным экономическим объектам, но за один и тот же период или момент времени. Примером таких данных явл сведения по разным фирмам (объем производства, численность работников, стоимость основных производственных фондов, прибыль за определенный период и т.д.).

Временными данными является набор сведений, характеризующих один и тот же объект, но в разные периоды или моменты времени. Примером таких данных явл данные о ежемесячных объемах грузооборота порта, о годовых объемах перевезенных грузов судоходной компанией, о среднегодовой себестоимости перевозки одной тонны груза по судоходной компании за ряд лет.

Переменные, участвующие в эконометрической модели, разделяются на следующие виды:

1) текущие экзогенные или независимые переменные (xt), значения которых задаются извне модели на данный момент времени t;

2) текущие эндогенные или зависимые переменные (yt), значения которых определяются внутри модели на данный момент времени t;

3) лаговые (экзогенные (xt-1, xt-2 и т.д.) или эндогенные переменные(yt-1, yt-2 и т.д.)), датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными;

4) предопределенные (объясняющие) переменные, к которым относятся текущие экзогенные переменные (xt), лаговые экзогенные переменные (xt-1, xt-2 и т.д.), а также лаговые эндогенные переменные (yt-1, yt-2 и т.д.)

Любая эконометрическая модель объясняет значения текущих эндогенных переменных в зависимости от предопределенных переменных.

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

y — зависимая переменная;
x — независимая переменная;
β — коэффициенты, которые необходимо найти с помощью МНК;
ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
Неоднородность дисперсии — Тест Уайта, , при \chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

points — Рейтинг статьи
reads — Число просмотров.
comm — Число комментариев.
faves — Добавлено в закладки.
fb — Поделились в социальных сетях (fb + vk).
bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

источники:

http://lektsii.org/10-54244.html

http://habr.com/ru/post/350668/