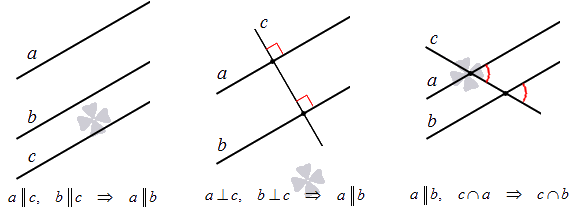Прямая на плоскости и ее уравнения конспект

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

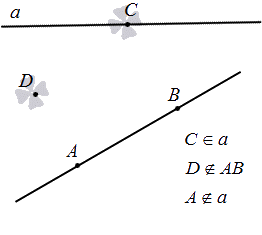
На каждой прямой и в каждой плоскости могут быть отмечены точки.

Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d .

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Чтобы обозначить, принадлежит точка плоскости или точка прямой, используют знак « ∈ ». Если в условии дано, что точка A лежит на прямой a , тогда это имеет такую форму записи A ∈ a . В случае, когда точка А не принадлежит, тогда другая запись A ∉ a .

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В , то прямую, проходящую через них можно назвать данными буквами, например, прямая А В . Рассмотрим рисунок, приведенный ниже.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Если дано, что точки А и Р – концы отрезка, значит, его обозначение примет вид Р А или А Р . Так как обозначения отрезка и прямой совпадают, рекомендовано дописывать или договаривать слова «отрезок», «прямая».

Краткая запись принадлежности включает в себя использование знаков ∈ и ∉ . Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂ . Если в условии дано, что отрезок А Р принадлежит прямой b , значит, и запись будет выглядеть следующим образом: А Р ⊂ b .

Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А , В , С , которые принадлежат одной прямой, а точка В лежит между А и С , следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Любая точка O , находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O , а другие – по другую сторону луча.

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

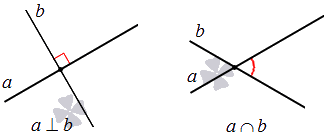
Две прямые на плоскости могут пересекаться.

Данный случай показывает, что имеется одна общая точка, которую называют пересечением прямых. Вводится обозначение пересечение знаком ∩ . Если имеется форма записи a ∩ b = M , то отсюда следует, что заданные прямые a и b пересекаются в точке M .

При пересечении прямых имеем дело образовавшимся углом. Отдельному рассмотрению подвергается раздел пересечения прямых на плоскости с образованием угла в 90 градусов, то есть прямого угла. Тогда прямые называют перпендикулярными. Форма записи двух перпендикулярных прямых такая: a ⊥ b , а это значит, что прямая a перпендикулярна прямой b .

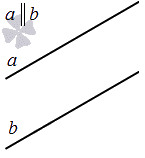
Две прямые на плоскости могут быть параллельны.

Только в том случае, если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны. Используется обозначение, которое можно записать при заданной параллельности прямых a и b : a ∥ b .

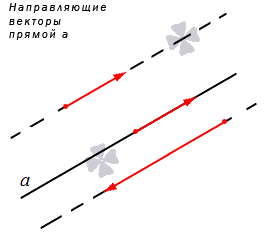
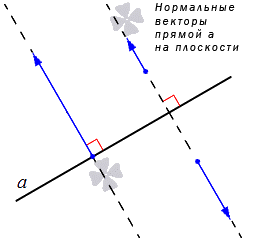
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

если две прямые параллельны третьей, тогда они все параллельны;
если две прямые перпендикулярны третьей, тогда эти две прямые параллельны;
если на плоскости прямая пересекла одну параллельную прямую, тогда пересечет и другую.

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

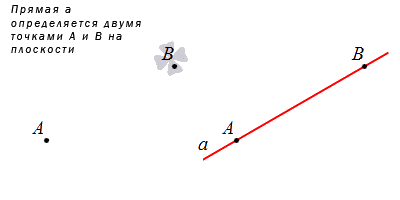
Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

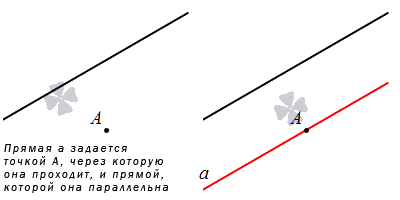
Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

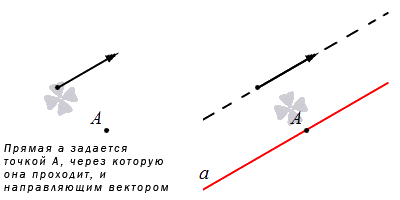
Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

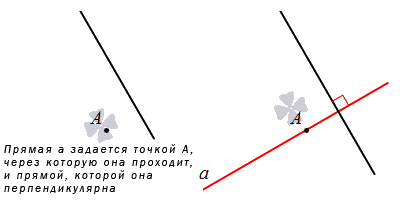
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

План занятия «Уравнение прямой на плоскости»

Просмотр содержимого документа
«План занятия «Уравнение прямой на плоскости»»

Министерство образования Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение «Ставропольский региональный многопрофильный колледж»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ЗАНЯТИЯ ПО ТЕМЕ

«УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ»

ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ

09.02.03 Программирование в компьютерных сетях

Иванова Владлена Сергеевна

Методическая разработка занятия

Специальность: 09.02.03 Программирование в компьютерных сетях

Преподаватель: Иванова Владлена Сергеевна

Дисциплина: ЕН.01 Элементы высшей математики

Наименование раздела: Элементы аналитической геометрии

Тема занятия: Уравнения прямой на плоскости

Вид: Практическое занятие

Тип занятия: Повторение и закрепление

Цель занятие: составить различные виды уравнений прямой на плоскости.

ПК 1.1. Выполнять разработку спецификаций отдельных компонент

ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Требования к умениям (практическому опыту): студент должен уметь составлять уравнения прямой на плоскости следующих видов: общее уравнение прямой; уравнение прямой в отрезках; уравнение с угловым коэффициентом; уравнение в канонической форме; уравнение прямой, проходящей через две данные точки; параметрические уравнения; нормальное уравнение. Разработать алгоритм составления уравнения прямой на плоскости.

Цели самостоятельной работы: формирование умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности.

Фронтальная работа (работа в группах и индивидуально)

Обсуждение деталей схематического изображения

Методы и приемы обучения: словесные, наглядные, информационные, компьютерные, объяснительно-иллюстративные, метод алгоритмических предписаний, мозговой штурм, прием «Ромашка Блума», рефлексия, прием из кинезиологического комплекса «Зеркальное рисование».

карточки для самостоятельной работы;

задания для выполнения на уроке;

задания для самопроверки;

Организационный момент (5 мин.)

Взаимные приветствия преподавателя и студентов; фиксация отсутствующих в учебном журнале; проверка внешнего состояния кабинета.

Проверка подготовленности студентов к занятию, их настроя на работу. Инструктирование по работе с оценочным листом (в котором в ходе работы оценивается работа каждой пары (за каждый правильный ответ студент получает наклейку «лайк». Оценка ставится паре, набравшей необходимое количество «лайков». 3 наклейки – удовлетворительно, 4 наклейки – хорошо, 6 наклеек – отлично)

САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ

1.Актуализация опорных знаний (35 мин.)

ЗАДАНИЕ №1. (Время выполнения – 5 мин.)

Закрепление знаний предыдущей темы «Основы алгебры векторов» с использованием приема – поиск соответствий.

Правильно соотнести определение и формулу: орт; модуль (длина) вектора; скалярное произведение векторов.

ЗАДАНИЕ №2. (Время выполнения – 15 мин.)

Повторение основных понятий лекции «Уравнения прямой на плоскости» с использованием приема «Ромашка Блума» (Студенты работают в парах. За каждый правильный ответ пара получает по «лайку»)

1 лепесток: Что мы изучили на прошлой лекции? Что называют уравнением прямой на плоскости?

2 лепесток: Какие именно виды уравнений прямой на плоскости мы изучили?

3 лепесток: Почему нормальное уравнение прямой так называется?

4 лепесток: Всегда ли общее уравнение прямой на плоскости проходит через начало координат?

5 лепесток: Что будет, если общее уравнение прямой на плоскости разделить на –С?

6лепесток: Как вы найдете расстояние от точки до прямой?

ЗАДАНИЕ №3. (Время выполнения – 3 мин.)

Проведение упражнения из кинезиологического комплекса «Зеркальное рисование».

Необходимо положить на стол чистый лист бумаги. Студенты рисуют одновременно обеими руками зеркально-симметричные рисунки (квадраты, треугольники, горизонтальные линии), буквы. При выполнении этого упражнения они почувствуют, как расслабляются глаза и руки. Когда деятельность обоих полушарий синхронизируется, заметно увеличится эффективность работы всего мозга.

Прослушать подготовленное студентами мини-сообщение на тему:

взаимное расположение прямых в пространстве: пересекающиеся прямые, параллельные прямые, скрещивающиеся прямые.

Решить задачу: сторона АС треугольника АВС параллельно плоскости а, а его стороны пересекают плоскость в точках M и N. Доказать, что треугольник АВС и MBN подобны.

2.Решение практических задач (Время выполнения – 42 мин.)

Игра «Моя геометрия». Алгоритм игры:

На экране появляется таблица (9 ячеек) с разной «стоимостью» задания (1 «лайк», 2 «лайка», 3 «лайка»)

Студенты выбирают «стоимость» и получают задание, которое нужно решить.

Если задание было решение у доски в полной мере, студент получает определенное количество лайков.

1 лайк (Составить общее уравнение прямой на плоскости)

3 лайка (Составить уравнение прямой, проходящей через две данные точки

3 лайка (Составить уравнение в параметрической форме)

2 лайка (Составить уравнение прямой в отрезках)

1 лайк (Составить неполное уравнение общей прямой)

2 лайка (Составить уравнение с угловым коэффициентом)

3 лайка (Составить уравнение прямой в каноничной форме)

3 лайка (Составить нормальное уравнение в прямой)

1 лайк (Найти расстояние между прямой и точкой)

Конспект занятия по теме «Различные уравнения прямой на плоскости»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Различные виды уравнения прямой на плоскости

1 Общее уравнение прямой на плоскости имеет вид

2 Уравнение прямой с угловым коэффициентом записывается в виде

где , — угол, который прямая образует с положительным направлением оси ОХ, — ордината точки пересечения прямой с осью ОУ.

3 Уравнение прямой , проходящей через данную точку в данном направлении имеет вид

где , — угол, который прямая образует с положительным направлением оси ОХ.

5 Уравнение прямой в отрезках имеет вид

где и — длины отрезков (с учетом знаков), отсекаемых прямой на осях ОХ и ОУ соответственно.

6 Угол между прямыми на плоскости

Пусть даны две прямые и .

Тангенс угла между прямыми и вычисляют по формуле

7 Условие параллельности прямых на плоскости

8 Условие перпендикулярности прямых на плоскости

9 Расстояние от точки М ₀ (х ₀ ; у ₀ ) до прямой Ах + Ву + С = 0 определяется по формуле

Решение типового примера:

Даны координаты вершин Δ АВС А(-2;2), В(1;6), С(2;4).

1) длину стороны АВ;

2) уравнения сторон АВ и ВС и их угловые коэффициенты;

3) внутренний угол В;

4) уравнение медианы АЕ;

5) уравнение и длину высоты С D ;

6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М, её пересечение с высотой С D .

1) Расстояние d между точками А( x ₁ ; y ₁ ) и В( x _2; y ₂ ) определяется по формуле .

Воспользовавшись ей, находим длину стороны АВ

= = = 5.

2) Уравнение прямой, проходящей через две заданные точки плоскости и имеет вид: .

Поэтому АВ: .

Угловой коэффициент k прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом: .

откуда .

Найдем уравнение прямой ВС

; ;

(ВС).

Приведем к виду : ; .

3) Для определения В треугольника АВС воспользуемся формулой

;

, .

4) Для составления уравнения медианы АЕ найдем координаты точки Е – середины стороны ВС по формулам: ; .

; ; .

Уравнение медианы АЕ:

А(-2;2), Е .

(АЕ).

5) Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку М ₀ с заданным угловым коэффициентом k и условием перпендикулярности прямых АВ и CD которая выражается соотношением , откуда .