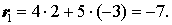Глава VIII
1. Прямые и плоскости в пространстве R n
Изучим пространство R n с другой точки зрения. Будем рассматривать его элементы не как векторы, а как точки, то есть А(х1, х2, . хn), где хi — координаты точки А ( i = 1, 2, . n). О(0. 0) — назовем началом координат.
Элементы R, R 2 , R 3 можно интерпретировать как координаты точек соответственно на прямой, на плоскости, в пространстве; поэтому R принято называть числовой прямой, R 2 — числовой плоскостью, R 3 — числовым пространством.
Как мы уже знаем, при n>3 непосредственное обращение к геометрии невозможно, но многие факты, относящиеся к R n , носят общий характер, не зависящий от n. Так свойства решений линейных уравнений и методы их исследования не зависят от числа переменных. Тогда можно сказать, что в этом смысле пространство R n обладает геометрическими свойствами, подобными свойствам пространств R, R 2 , R 3 . Множества точек в R 4 (“фигуры”) будем задавать с помощью уравнений, неравенств с n переменными и их систем как области их решений.
Определение 1. Область решений совместной системы линейных уравнений с n переменными ранга r назовем k-мерной плоскостью в R n , где k = n — r (k — число свободных, а r — базисных переменных.)
Отметим два случая:
1. r = n, k = 0. Система имеет единственное решение, которое представляет собой точку в R n , то есть точку можно считать нуль-мерной плоскостью.
2. r = 0, k = n. Все уравнения являются тождествами (0 = 0), все переменные свободные, область решений системы совпадает со всем пространством R n , то есть само пространство можно считать n-мерной плоскостью.
Если этих два крайних случая исключить из рассмотрения, то очевидно, что k может меняться в пределах 1 £ k £ n — 1.
Определение 2. Плоскость наибольшей возможной в R n размерности, но не совпадающей со всем пространством, то есть (n-1)-мерную плоскость, называют гиперплоскостью, а плоскость наименьшей возможной размерности, но не являющуюся точкой, то есть одномерную плоскость, называют прямой.
R — само одномерно и в нем не может быть плоскостей меньшей размерности.
R 2 — (числовая плоскость) — в нем гиперплоскость совпадает с прямой — это одномерная плоскость.
R 3 — (числовое пространство) — здесь гиперплоскостью является двухмерная плоскость, а прямой — одномерная плоскость; других плоскостей нет.
З а м е ч а н и е. При n > 3 кроме гиперплоскостей и прямой существуют плоскости промежуточных размерностей (n-2)-мерные, . трехмерные, двухмерные.
Гиперплоскость обычно задают одним линейным уравнением
в котором не все коэффициенты равны нулю, то есть

Условие (1.2) равносильно тому, что ранг системы, состоящей из одного уравнения (1.1), равен 1.
Пусть теперь система состоит из двух уравнений

Если ее матрица А имеет ранг 1, то
В этом случае гиперплоскости, определенные уравнениями системы (1.3), называются параллельными и, если

(то есть ранг расширенной матрицы равен 2), то система несовместна:
гиперплоскости, определенные уравнениями системы (1.3), не имеют общих точек (не пересекаются); если же

(то есть ранг расширенной матрицы равен 1), то система сводится к одному уравнению, две гиперплоскости совпадают.
И наконец, если ранг матрицы А равен 2, то система определяет (n-2)-мерную плоскость.
Прямую можно задать совместной системой линейных уравнений с n переменными ранга r = n-1. Если известны две точки А(а1,а2. аn), B(b1,b2. bn) прямой, то эту систему можно записать в виде

где X(x1, x2, . xn) — текущая переменная точка прямой.
Систему уравнений (1.4) называют уравнениями прямой, проходящей через две точки А и В.
1.1. Расстояние от точки до прямой
Рассмотрим прямую l в R 2 , заданную уравнением
А × х + В × у + С = 0
и точку М(х1,у1) вне данной прямой.
Обозначим через d расстояние MN (MN перпендикуляр к l). Уравнение перпендикуляра можно записать в виде В × (х — х1) — А × (у — у1) = 0.


то есть t — коэффициент пропорциональности. Поэтому из (1.5) следует, что

C другой стороны, точка N(x2,y2) принадлежит l, следовательно, из (1.5) получаем
Подставим эти значения в уравнение прямой А × х + В × у + С = 0. Получим
А × х2 + В × у2 + С = А × (х1 + А × t) + В × ( y1 + В × t) + С = (А × х1 + В × у1 + C) + t × (А 2 + В 2 ) = 0


З а м е ч а н и е. (следствие).

является расстоянием от прямой до начала координат.
2. Разделив обе части общего уравнения прямой на 

свободный член которого 
1.2. Нормированное уравнение прямой
Пусть дана прямая l. Проведем через начало координат прямую n, перпендикулярную l. Пусть Р — точка пересечения прямых. Возьмем единичный вектор 
Выразим уравнение l через два параметра:

Пусть М(х,у) принадлежит l. Тогда проекция 








Следовательно, точка М принадлежит прямой l означает, что координаты этой точки удовлетворяют уравнению

Это и есть нормированное уравнение прямой l.
Пусть теперь имеем общее уравнение прямой l:
l: А × х + В × у + С = 0
l:
t × A = Cos q , t × B = Sin q , t × C = -p.
t 2 × A 2 + t 2 × В 2 = Cos 2 q + Sin 2 q = 1
t 2 × (A 2 + В 2 ) = 1 (1.9)

Следовательно, чтобы получить из общего уравнения прямой
А × х + В × у + С = 0
нормированное уравнение (1.8) следует умножить его на нормирующий множитель (1.9), знак которого противоположен С.
2. Общее уравнение плоскости в R 3
Зафиксируем произвольную декартову прямоугольную систему координат Oxyz и рассмотрим произвольное уравнение первой степени
А × х + В × у + С × z + D = 0, (2.1)
где A, B, C, D — произвольные константы, хотя бы одна из которых не равна 0.
Уравнение (2.1) заведомо имеет хотя бы одно решение (x0, y0, z0).
Действительно, пусть С ¹ 0, следовательно, взяв произвольные (x0, y0), мы получим 
которое эквивалентно (2.1).
Рассмотрим разность между (2.1) и (2.2).
которое эквивалентно (2.1).
Докажем, что уравнение (2.2) и, стало быть, уравнение (2.1), определяет плоскость (П) в Oxyz.

то есть хотя бы одна координата его не равна 0.
Возьмем произвольную точку М0(x, y, z), принадлежащую плоскости П, то есть ее координаты удовлетворяют уравнению (2.3), ибо в этом случае вектор 


Если точка М(x,y,z) не принадлежит плоскости П, то ее координаты не удовлетворяют (2.3), ибо в этом случае вектор 

Таким образом, мы доказали следующее утверждение.
Теорема 2.1. Если в R 3 фиксирована произвольная декартова система координат Oxyz (прямоугольная), то всякое уравнение первой степени с тремя переменными x,y,z определяет относительно этой системы плоскость.
З а м е ч а н и я.
1. Уравнение (2.1) с произвольными коэффициентами А, В, С (хотя бы один из которых не должен быть равен нулю) называется общим уравнением плоскости в R 3 .
2. Если два общих уравнения
А × х + В × у + С × z + D = 0
определяют одну и ту же плоскость, следовательно, существует число t, такое, что справедливы равенства
Рассмотреть(самостоятельно) неполные уравнения плоскости, когда
1) А = 0; 2) В = 0; 3) C = 0; 4) D = 0;
5) A = В = 0; 6) A = C = 0; 7) B = C = 0;
8) A = В = C = 0; 9) A = C = D = 0; 10) В = C = D = 0;
2.1. Угол между двумя плоскостями
Пусть даны две плоскости П1 и П2, которые заданы уравнениями
Чтобы определить угол между плоскостями, достаточно определить угол j между их нормальными векторами 

По определению скалярного произведения

Условие параллельности двух плоскостей заключается в пропорциональности координат векторов 


Условие “плоскость П1 перпендикулярна к плоскости П2” определяет, что Cos j = 0
2.2. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой
Пусть даны три точки М1(x1,y1,z1), М2(x2,y2,z2) и М3(x3,y3,z3). Необходимо вывести уравнение плоскости, проходящей через эти три точки. Так как эти три точки не лежат на одной прямой, то векторы 




Теорема 2.2. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы выполнялось следующее условие

Из условия (2.8) получим уравнение первой степени относительно x,y,z. Оно и является уравнением искомой плоскости.
2.3. Нормированное уравнение плоскости. Отклонение точки от плоскости
Пусть дана плоскость П. Проведем через начало координат прямую n перпендикуляр к плоскости П, и пусть Р — точка пересечения прямой n и плоскости П.
Рассмотрим вектор 






прn 

Так как 

Определение 2.1. Назовем отклонением d точки М от плоскости П число +d в случае, когда точка М и начало координат точка О лежат по разные стороны от плоскости П, и число -d — в случае, когда точка М и начало координат точка О лежат по одну сторону от плоскости П, (куда направлен вектор 
Для нахождения отклонения d точки М0(x0,y0,z0) от плоскости П следует в левую часть нормированного уравнения плоскости П поставить на место х,у,z координаты x0,y0,z0 точки М.
А × х + В × у + С × z + D = 0
определяют одну ту же плоскость, то существует t такое, что
t × A = Cos a , t × B = Sin b , t × C = Sin g , t × D = -p.
Так как сумма квадратов направляющих косинусов равна 1, то
t 2 × (A 2 + B 2 + C 2 )=1,

где знак t противоположен знаку коэффициента D.
Для приведения общего уравнения плоскости
А × х + В × у + С × z + D = 0
к нормированному виду (2.9) следует умножить его на нормирующий множитель (2.10), знак которого противоположен знаку коэффициента D.
3. Прямая линия R 3
Прямую в пространстве R 3 можно задать как пересечение двух плоскостей, определяемых уравнениями

Приведем (3.1) к каноническому виду.
Для этого достаточно найти:
1) хотя бы одну точку М1(x1,y1,z1), через которую проходит прямая
Так как плоскости, определяемые (3.1), не параллельны и не сливаются, то нарушается (2.6), то есть хотя бы одна из пропорций

а это значит, что хотя бы один из определителей второго порядка


отличен от нуля.

Тогда, взяв вместо z произвольное число z1 и подставив его в уравнение (3.1), можно определить соответственно x1 и y1

Можно взять z1=0. Тогда, воспользовавшись (3.2), получим, что прямая проходит через точку 
Пусть текущая точка М(x,y,z). Тогда уравнение линии можно записать в виде


Уравнение прямой, проходящей через данную точку М1(x1,y1,z1) и перпендикулярной плоскости А × х + В × у + С × z + D = 0, имеет вид

Уравнение прямой, параллельной данной плоскости и проходящей через данную точку М0(x0,y0,z0).
Пусть плоскость П задана уравнением
Тогда уравнение прямой имеет вид
4. Выпуклые множества точек на плоскости. Неравенства
4.1. Неравенства
Пусть задана линия
то есть это множество точек, координаты которых удовлетворяют этому уравнению. Аналогично можно рассмотреть множество точек, координаты которых удовлетворяют неравенству

Это уравнение определяет окружность с центром в точке С(a,b) радиуса r, (Рис. 8.4);
(х — a) 2 + (х — b) 2 — r 2 0
определяет множество точек, лежащих внутри круга с центром в точке С(a,b) радиуса r, (Рис. 8.5);
(х — a) 2 + (х — b) 2 — r 2 > 0
определяет множество точек, лежащих вне этого круга с центром в точке С(a,b) радиуса r (Рис. 8.6);
Множество точек, удовлетворяющих (4.1), называют областью решений этого уравнения.
Аналогично будем говорить об области решений неравенств (4.2) и (4.3).
Пусть теперь F(x, y) — линейное уравнение, то есть имеет вид
F(x, y) = A × x + B × y + C, (4.4)
где A, B, C — константы .
Любое невырожденное уравнение A × x + B × y + C = 0 определяет линию L в R 2 , рассмотрим
A × x + B × y + C 0 (4.5)
A × x + B × y + C > 0, (4.6)
По отношению к прямой линии все точки разбились на два множества Ф1 и Ф2, лежащие по разные стороны от прямой L (Рис 8.7).
Покажем, что эти множества определяются неравенствами (4.5) и (4.6).
Так как эти точки не лежат на прямой, то имеем
Действительно, так как точки М1(х1,у1), М2(х2,у2) лежат по разные стороны от прямой (4.4), то существует точка М0(х0,у0) такая, что она делит отрезок М1М2 в отношении 


Так как точка М0(х0,у0) принадлежит прямой L, то имеем
Подставим (4.7) в (4.4):

то есть d 1+ l × d 2 = 0, откуда d 1 = -l × d 2 , но l > 0, следовательно, d 1 и d 2 имеют разные знаки.
Пусть, например, d 1 0, d 2 > 0, тогда точка М1(х1,у1) удовлетворяет неравенству (4.5), а точка М2(х2,у2) — неравенству (4.6).
Множество точек, лежащих на некоторой прямой и по одну сторону от нее, называют полуплоскостью.
Очевидно, что каждая прямая L разбивает плоскость П на две полуплоскости, для которых она является общей границей. Считается, что граница принадлежит сразу двум полуплоскостям.
Если (4.4) — это граница, то нестрогие неравенства
A × x + B × y + C £ 0
A × x + B × y + C ³ 0
Пусть задана система неравенств

Геометрически система (4.8) может быть истолкована как область решений этой системы, то есть это множество точек , которые одновременно удовлетворяют всем неравенствам этой системы, то есть 

З а м е ч а н и е. В частности может иметь место 
Областью решений системы линейных неравенств

является очевидно пересечение полуплоскостей, определяемых каждым из неравенств.
Эту область будем называть многоугольником.
Не исключены также случаи вырождения многоугольной области в прямую или луч, а многоугольника — в отрезок или точку.
4.2. Выпуклые множества точек на плоскости
Определение 4.1. Множество точек называется выпуклым, если вместе с двумя его точками М1 и М2 ему принадлежат и все внутренние точки отрезка М1М2.
Выпуклые множества: полуплоскость, круг, отрезок и так далее.
Многоугольники могут быть как выпуклые, так и невыпуклые. Геометрически это можно всегда увидеть, но этот факт также может быть
установлен и аналитически.
Теорема 4.1. Пусть дана полуплоскость
Ф1: A × x + B × y + C 0
Если А × х0 + В × у0 + С 0, то тогда полуплоскость будет выпуклой.
Д о к а з а т е л ь с т в о :
Координаты точки М1 можно выразить через координаты точек М1 и М2:


Подставим эти выражения в неравенство полуплоскости

l > 0, 
а по определению 8.4 такое множество называется выпуклым.
З а м е ч а н и е. Определение выпуклого множества сформулировано в предположении, что в этом множестве имеются по крайней мере две точки. Если множество пустое (в этом случае его обозначают как Æ ) или состоит из одной точки, то его тоже считают выпуклым.
Для выпуклых множеств имеет место следующая теорема:
Теорема 4.2. Пересечение любого числа выпуклых множеств — выпуклое множество.
Д о к а з а т е л ь с т в о :
Пусть j 1, j 2, . j n — выпуклые множества и их пересечение 

Пусть имеем две произвольные точки М1(х1,у1) и М2(х2,у2), принадлежащие пересечению множеств j i, тогда, так как все множества j i выпуклы, то им принадлежит и отрезок М1М2, а следовательно, 

Следствие. Область решений системы линейных неравенств (), если она не представляет собой Æ , является выпуклой многоугольной областью или выпуклым многоугольником.
5. Выпуклые множества в пространстве. Неравенства
По аналогии с пространством R 2 можно рассмотреть геометрию и неравенства в пространстве R 3 .
определяют множество точек пространства, координаты которых удовлетворяют этим неравенствам.
(х — a) 2 + (х — b) 2 + (z — c) 2 2
определяет внутреннюю область шара, ограниченную сферой
(х — a) 2 + (х — b) 2 + (z — c) 2 = r 2
с центром в точке С(а,b,c) и радиусом r, а неравенство
(х — a) 2 + (х — b) 2 + (z — c) 2 > r 2
определяет множество точек, находящихся вне этого шара.
Множество точек, лежащих в некоторой плоскости и по одну сторону от нее, называют полупространством.
5.1. Нестрогие линейные неравенства
D + A × x + B × y + C × z и
D + A × x + B × y + C × z > 0
определяют два полупространства, общей границей которых будет плоскость
D + A × x + B × y + C × z = 0.
Доказательство этого факта проводится так же, как и в случае двух переменных.
Пусть дана система линейных неравенств с тремя неизвестными

Областью решений системы (5.3) является пересечение полупространств, то есть такое множество точек, если оно не пусто, которое является решением каждого из неравенств системы. Это пересечение полупространств называют многогранной областью или (в случае ограниченности) многогранником.
З а м е ч а н и е.
1. Понятие выпуклого множества точек и теорема о выпуклости пересечения выпуклых множеств точек сохраняет силу и для пространства.
(Провести доказательство самостоятельно).
2. Так как полупространство выпукло, то область решений системы линейных неравенств (5.3), если она не пуста, является выпуклой многогранной областью (или выпуклым многогранником), если она ограничена.
Не исключены случаи вырождения.

Канонические уравнения прямой в пространстве: теория, примеры, решение задач
Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.
В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.
Что такое каноническое уравнение прямой в пространстве
О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.
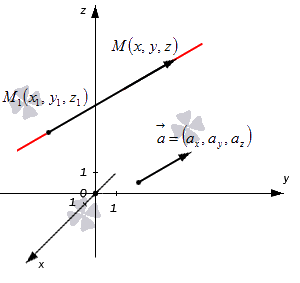
Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,
Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:
M 1 M → = x — x 1 , y — y 1 , z — z 1
После этого нужное нам условие мы можем сформулировать так: M 1 M → = x — x 1 , y — y 1 , z — z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z
Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.
При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z
Между правыми частями после этого можно будет поставить знак равенства:
x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z
В итоге у нас получились уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.
Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.
Если один-два параметра a равны 0 , то уравнение x — x 1 a x = y — y 1 a y = z — z 1 a z носит условный характер. Его следует считать равным следующей записи:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .
Частные случаи канонических уравнений мы разберем в третьем пункте статьи.
Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.
1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:
x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 2 a x = y — y 2 a y = z — z 2 a z .
2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 1 μ · a x = y — y 1 μ · a y = z — z 1 μ · a z .
Вот несколько примеров таких уравнений с заданными значениями:
x — 3 2 = y + 1 — 1 2 = z ln 7
Тут x 1 = 3 , y 1 = — 1 , z 1 = 0 , a x = 2 , a y = — 1 2 , a z = ln 7 .
x — 4 0 = y + 2 1 = z + 1 0
Тут M 1 ( 4 , — 2 , — 1 ) , a → = ( 0 , 1 , 0 ) .
Как составить каноническое уравнение прямой в пространстве
Мы выяснили, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.
Разберем пару конкретных задач.
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z — 3 — 5 . Запишите координаты всех направляющих векторов для нее.
Решение
Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , — 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , — 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).
Ответ: 4 · μ , 2 · μ , — 5 · μ , μ ∈ R , μ ≠ 0
Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , — 3 , 2 ) и имеет направляющий вектор с координатами — 1 , 0 , 5 .
Решение
У нас есть данные, что x 1 = 0 , y 1 = — 3 , z 1 = 2 , a x = — 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.
x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 0 — 1 = y — ( — 3 ) 0 = z — 2 5 ⇔ ⇔ x — 1 = y + 3 0 = z — 2 5
Ответ: x — 1 = y + 3 0 = z — 2 5
Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.
Канонические уравнения с одним или двумя a, равными нулю
Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x — x 1 a x = y — y 1 a y = z — z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:
- В первом случае:
x — x 1 0 = y — y 1 a y = z — z 1 a z = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x — x 1 = 0 y — y 1 a y = z — z 1 a z = λ
Во втором случае:
x — x 1 a x = y — y 1 0 = z — z 1 a z = λ ⇔ x = x 1 + a x · λ y — y 1 = 0 z = z 1 + a z · λ ⇔ y — y 1 = 0 x — x 1 a x = z — z 1 a z = λ
В третьем случае:
x — x 1 a x = y — y 1 a y = z — z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z — z 1 = 0 ⇔ z — z 1 = 0 x — x 1 a x = y — y 1 a y = λ
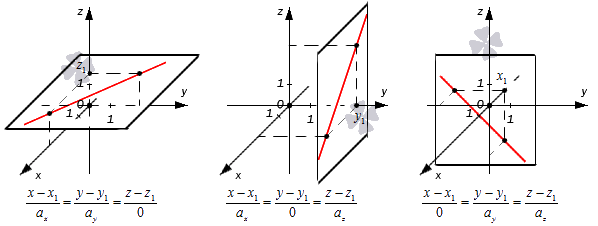
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x — x 1 = 0 , y — y 1 = 0 или z — z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.
Следовательно, мы сможем записать канонические уравнения немного иначе.
- В первом случае: x — x 1 0 = y — y 1 0 = z — z 1 a z = λ ⇔ x — x 1 = 0 y — y 1 = 0 z = z 1 + a z · λ , λ ∈ R
- Во втором: x — x 1 0 = y — y 1 a y = z — z 1 0 = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ , λ ∈ R z — z 1 = 0
- В третьем: x — x 1 a x = y — y 1 0 = z — z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z — z 1 = 0
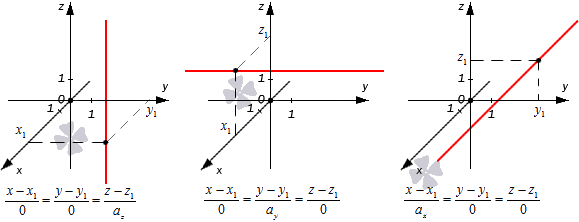
Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:
Покажем на примерах, как применяются эти правила.
Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .
Решение
Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.
Для прямой O x : x 1 = y 0 = z 0
Для прямой O y : x 0 = y 1 = z 0
Для прямой O z : x 0 = y 0 = z 1
Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .
В пространстве задана прямая, которая проходит через точку M 1 ( 3 , — 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.
Решение
Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:
x — 3 0 = y — ( — 1 ) 1 = z — 12 0 ⇔ x — 3 0 = y + 1 1 = z — 12 0
Ответ: x — 3 0 = y + 1 1 = z — 12 0
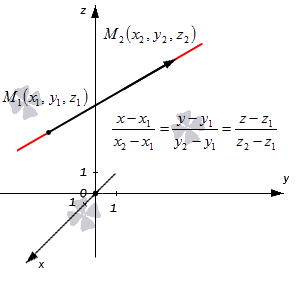
Как записать каноническое уравнение прямой, которая проходит через две заданные точки
Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?
Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:
M 1 M 2 → = x 2 — x 1 , y 2 — y 1 , z 2 — z 1
Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:
x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1
Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:
Приведем пример решения задачи.
в пространстве есть две точки с координатами M 1 ( — 2 , 4 , 1 ) и M 2 ( — 3 , 2 , — 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.
Решение
Согласно условиям, x 1 = — 2 , y 1 = — 4 , z 1 = 1 , x 2 = — 3 , y 2 = 2 , z 2 = — 5 . Нам требуется подставить эти значения в каноническое уравнение:
x — ( — 2 ) — 3 — ( — 2 ) = y — ( — 4 ) 2 — ( — 4 ) = z — 1 — 5 — 1 ⇔ x + 2 — 1 = y + 4 6 = z — 1 — 6
Если мы возьмем уравнения вида x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , то у нас получится: x — ( — 3 ) — 3 — ( — 2 ) = y — 2 2 — ( — 4 ) = z — ( — 5 ) — 5 — 1 ⇔ x + 3 — 1 = y — 2 6 = z + 5 — 6
Ответ: x + 3 — 1 = y — 2 6 = z + 5 — 6 либо x + 3 — 1 = y — 2 6 = z + 5 — 6 .
Преобразование канонических уравнений прямой в пространстве в другие виды уравнений
Иногда пользоваться каноническими уравнениями вида x — x 1 a x = y — y 1 a y = z — z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.
Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:
x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ z — z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.
В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x — 2 3 = y — 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.
Решение
Сначала приравниваем каждую часть дроби к λ .
x — 2 3 = y — 2 = z + 7 0 ⇔ x — 2 3 = λ y — 2 = λ z + 7 0 = λ
Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:
x — 2 3 = λ y — 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7 + 0 · λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7
Ответ: x = 2 + 3 · λ y = — 2 · λ z = — 7
Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).
Равенство x — x 1 a x = y — y 1 a y = z — z 1 a z нужно для начала представить в виде системы уравнений:
x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a x y — y 1 a y = z — z 1 a z
Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:
x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a z y — y 1 a y = z — z 1 a z ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) a z · ( x — x 1 ) = a x · ( z — z 1 ) a z · ( y — y 1 ) = a y · ( z — z 1 ) ⇔ ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0
В итоге у нас вышло, что:
x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0
Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y — a x 0 a z 0 — a x 0 a z — a y = 0 и один из определителей второго порядка не равен 0 :
a y — a x a z 0 = a x · a z , a y 0 a z — a x = a x · a y , — a x 0 0 — a x = a x 2 a y — a x 0 a z = a y · a z , a y 0 0 — a y = — a y 2 , — a x 0 a z — a y = a x · a y a z 0 0 a z = a z 2 , a z — a x 0 — a y = — a y · a z , 0 — a x a z — a y = a x · a z
Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.
Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.
Прямая задана каноническим уравнением x — 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.
Решение
Начнем с попарного приравнивания дробей.
x — 1 2 = y 0 = z + 2 0 ⇔ x — 1 2 = y 0 x — 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x — 1 ) = 2 y 0 · ( x — 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0
Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x — 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .
Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x — 1 2 = y 0 = z + 2 0
Ответ: y = 0 z + 2 = 0
Прямая задана уравнениями x + 1 2 = y — 2 1 = z — 5 — 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.
Решение
Приравниваем дроби попарно.
x + 1 2 = y — 2 1 = z — 5 — 3 ⇔ x + 1 2 = y — 2 1 x + 1 2 = z — 5 — 3 y — 2 1 = z — 5 — 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y — 2 ) — 3 · ( x + 1 ) = 2 · ( z — 5 ) — 3 · ( y — 2 ) = 1 · ( z — 5 ) ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + 7 — 11 = 0
Получаем, что определитель основной матрицы полученной системы будет равен 0 :
1 — 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( — 2 ) · 2 · 0 + 0 · 3 · 3 — 0 · 0 · 0 — 1 · 2 · 3 — ( — 2 ) · 3 · 1 = 0
Минор второго порядка нулевым при этом не будет: 1 — 2 3 0 = 1 · 0 — ( — 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.
В итоге мы можем вычислить ранг основной матрицы системы x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:
x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0
Ответ: x — 2 y + 5 = 0 3 x + 2 z — 7 = 0
Прямые на координатной плоскости
 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
График линейной функции
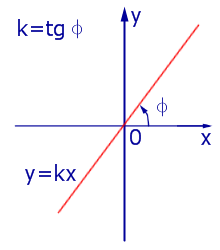
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
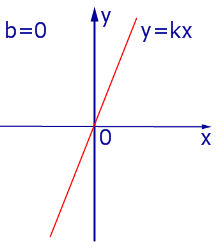 |
| Рис.1 |
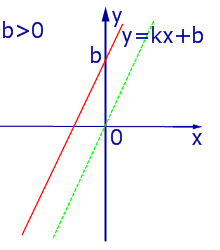 |
| Рис.2 |
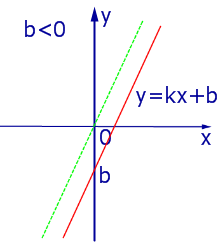 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
| Рис.4 |
 |
| Рис.5 |
 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
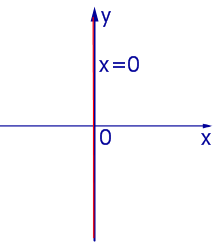
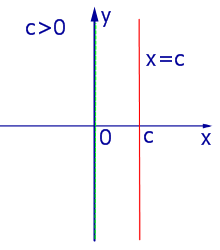
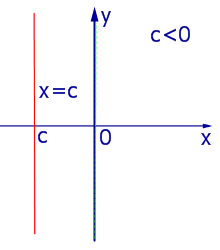
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство источники: http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/kanonicheskie-uravnenija-prjamoj-v-prostranstve/ http://www.resolventa.ru/spr/algebra/degree1.htm |











 , параллельны .
, параллельны .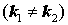 , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.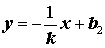
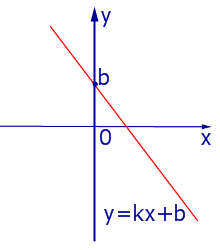
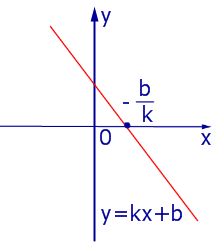
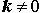 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле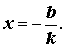
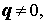 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .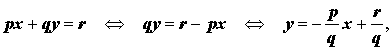
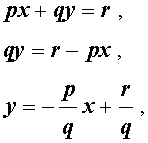
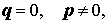 получаем:
получаем: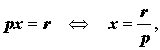
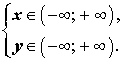
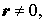 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.