Прямолинейная зависимость между двумя показателями задается уравнением

Однофакторный линейный корреляционно-регрессионный анализ

Корреляционная связь — это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных.

Наиболее разработанной в теории статистики является методология так называемой парной корреляции — зависимости между двумя случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению другой. Например, зависимость между производительностью труда и объемом производства, зависимость между размерами активов банка и суммой прибыли банка; ростом производительности труда и стажем работы сотрудников.

Для выявления и оценки связи между изучаемыми признаками в корреляционно-регрессионном анализе необходимо построить регрессионную модель (уравнение регрессии), которая лучше других будет отражать реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих исследований или осуществляться эмпирически – перебором и оценкой функций разных типов.

Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой (уравнение однофакторной корреляционной связи):

где х — факторный признак; y— результативный признак; а и b — неизвестные параметры уравнения регрессии.

Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание значений результативного показателя.

Параметры a и b оцениваются с помощью специальных методов, наибольшее распространение из которых получил метод наименьших квадратов, суть которого заключается в том, чтобы подобрать параметры уравнения ў_x=a + bx с таким расчетом, чтобы квадраты суммарных отклонений фактических значений ряда (y_x) от найденных по статистической модели (ў_x) были бы минимально возможными, то есть:

Для нахождения параметров a и b надо приравнять к нулю частные производные от полученного выражения по каждой искомой константе в отдельности. После соответствующих преобразований получают систему уравнений, которую называют нормальной:

где n— количество наблюдений.

Подставив в систему имеющуюся исходную информацию, рассчитываются параметры а и b.

Параметр a является свободной переменной и не несет никакого экономического смысла, а параметр b – коэффициент регрессии — при наличии прямой зависимости имеет положительное значение, а в случае обратной зависимости – отрицательное. Кроме того, он показывает, насколько в среднем изменяется величина результативного признака y при изменении факторного признака x на 1.

Например, по данным о стоимости оборудования (x) и производительности труда (y) методом наименьших квадратов получено уравнение:

В этом случае коэффициент b означает, что увеличение стоимости оборудования на 1 млн. руб. ведет в среднем к росту производительности труда на 2,08 тыс. руб.

Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака y при изменении факторного признака x на 1%:

.

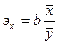
Для измерения тесноты связи между факторными и результативными показателями в однофакторном корреляционно-регрессионном анализе определяется коэффициент корреляции, который определяется по следующей формуле:

,

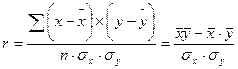
где х – факторный признак,

у — результативный признак,

– среднее квадратическое отклонение по признаку x,

– среднее квадратическое отклонение по признаку y.

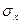
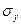
Коэффициент корреляции принимает значение в интервале от -1 до +1.

Если |r| 0,7 – сильная (тесная).

При |r|=1 связь называется функциональной, а при |r|=0 линейная связь между x и y отсутствует.

Квадрат коэффициента корреляции носит название коэффициента детерминации (R 2 ).

Величина коэффициента детерминации служит одним из критериев качества линейной модели. Чем ближе его значение к 1, тем меньше роль случайных факторов, и, следовательно, данную линейную модель можно использовать для прогноза значений результативного признака.

Дата добавления: 2017-11-04 ; просмотров: 491 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Прием процентных разностей является разновидностью метода _ для расчета влияния причин

Прием процентных разностей является разновидностью метода _ для расчета воздействия причин в детерминированном факторном анализе
(*ответ*) условных различий
nbsp;цепной подстановки
nbsp;безусловных различий
nbsp;долевого роли
Приказы управляющего о проведении функционально-стоимостного анализа определенного объекта, привлечении определенных тружеников к выполнению этой работы, вещественной заинтересованности тружеников по результатам анализа определяются на _ шаге
(*ответ*) предварительном
nbsp;аналитическом
nbsp;информационном
nbsp;творческом
Проведение поиска резервов планомерно, систематически, ежедневно, значит его
(*ответ*) непрерывность
nbsp;эффективность
nbsp;перспективность
nbsp;массовость
Проверка корректности дизайна данных для анализа хозяйственной деятельности, корректности арифметических подсчетов, соответствия показателей, которые содержатся в плановой документации, утвержденным плановым заданиям, согласованности показателей и т.д. является
(*ответ*) технической
nbsp;визуальной
nbsp;аналитической
nbsp;логической
Прямолинейная зависимость между двумя показателями задается уравнением
(*ответ*) прямой
nbsp;регрессии
nbsp;гиперболы
nbsp;параболы
Размещение изучаемых явлений либо объектов в определенном порядке с выявлением их связи и подчиненности является
(*ответ*) классификацией
nbsp;нумерацией
nbsp;детализацией
nbsp;классификацией
Разработка чертежей и набросков для производства опытных образцов; проектирование и изготовка специнструмента и оснастки; изготовка и испытание опытнейших образцов; разработка технической документации на изменение конструкции происходит на шаге _ функционально-стоимостного анализа
(*ответ*) внедрения
nbsp;рекомендательном
nbsp;испытательном
nbsp;творческом
Распределение прироста действенного показателя за счет конфигурации фактора первого уровня между факторами второго уровня может быть осуществлено методом
(*ответ*) пропорционального дробленья
nbsp;индексным
nbsp;равномерного рассредотачивания
nbsp;долевого роли
Расчет уравнения параболы второго порядка производится методом
(*ответ*) наименьших квадратов
nbsp;долевого участия
nbsp;последовательных замен
nbsp;цепных подстановок
Запасы, которые выявляются и могут быть использованы только на исследуемом предприятии, называются
(*ответ*) внутрихозяйственными
nbsp;региональными
nbsp;местными
nbsp;межхозяйственными

Прямолинейная регрессия, ее коэффициент и уравнение

ПРЯМОЛИНЕЙНАЯ РЕГРЕССИЯ, ЕЕ КОЭФФИЦИЕНТ И УРАВНЕНИЕ

При линейном типе связи между двумя изучаемыми признаками кроме расчета корреляций применяется расчет коэффициента регрессии.

В случае прямолинейной корреляционной связи каждому из изменений одного признака соответствует вполне определенное изменение другого признака. Однако коэффициент корреляции показывает эту связь лишь в относительных величинах — в долях единицы. С помощью же регрессионного анализа эту величину связи получают в именованных единицах. Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.

В отличие от корреляционного регрессионный анализ дает более широкую информацию, поскольку вычислением двух коэффициентов регрессии Rx/y и Rу/х возможно определить как зависимость первого признака от второго, так и второго от первого. Выражение регрессионной связи с помощью уравнения позволяет по определенному значению одного признака установить значение другого признака.

Коэффициент регрессии R представляет собой произведение коэффициента корреляции на отношение квадратических отклонений, вычисленных для каждого признака. Рассчитывается он по формуле

Rx/y = r ´

где, R — коэффициент регрессии; SХ — среднее квадратическое отклонение первого признака, который изменяется в связи с изменением второго; SУ — среднее квадратическое отклонение второго признака в связи с изменением которого изменяется первый признак; r — коэффициент корреляции между этими признаками; х — функция; у — аргумент.

По этой формуле определяется величина значения х при изменении у на единицу измерения. При необходимости обратного расчета можно найти величину у при изменении х на единицу измерения по формуле:

Rу/х = r ´

В этом случае активная роль в изменении одного признака по отношению к другому меняется, по сравнению с предыдущей формулой аргумент становится функцией и наоборот. Величины SX и SY принимаются в именованном выражении.

Между значениями г и R имеется четкая взаимосвязь, выражающаяся в том, что произведение регрессии х по у на регрессию у по х равно квадрату коэффициента корреляции, т. е.

Это свидетельствует, что коэффициент корреляции представляет собой среднюю геометрическую из обоих значений коэффициентов регрессии данной выборки. Данная формула может быть использована для проверки правильности расчетов.

При обработке цифрового материала на счетных машинах могут применяться развернутые формулы коэффициента регрессии:

Rx/y =;

Rx/y =

Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:

SR = ´Sr = ´

Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:

tR =

в итоге он равен критерию достоверности коэффициента корреляции:

tR = = = = tr

Достоверность величины tR устанавливается по таблице Стьюдента при n = n — 2, где n — число пар наблюдений.

Предположим, что при расчете коэффициента корреляции между уровнем яйценоскости и массой яиц:

было установлено, что r = -0,46;

для показателя яйценоскости: = 102; S = 7,0; n = 40

для показателя массы яйца: = 56,68; S = 1,94;n = 40

регрессия первого признака по второму равна:

Rx/y = ´(-0,46) = 3,61´(-0,46) = -1,66

Это означает, что увеличение массы яйца на 1 г в данной популяции кур сопровождается уменьшением яйценоскости за 5 мес. на 1,66 яйцо.

Ry/x = ´(-0,46) = 0,277´(-0,46) = -0,127

показывает, что повышение яйценоскости на 1 яйцо за 5-месячный период в данной популяции кур сопровождается уменьшением средней массы яиц на 0,127 г.

По формуле взаимозависимости r и R можно проверить правильность расчета:

(-1,66) ´ (-0,127) = 0,210; (-0,46)2 = 0,210.

Ошибка коэффициента регрессии Rx/y = равна

SR = ´Sr = ´

SR = 3,61´= 3,61´= 3,61´0,144 = 0,52

Критерий достоверности Rx/y равен

tR = = 3,19

По таблице Стьюдента стандартные значения t для n = 38 равны 2,0-2,7-3,6. Следовательно, рассчитанный коэффициент регрессии достоверен при Р ³ 0,99.

Более глубокий анализ связи двух признаков может быть сделан на основе расчета уравнения прямолинейной регрессии. Сущность коэффициента прямолинейной регрессии, показывающей насколько второй признак отклоняется от своей средней, если первый отклоняется от своей средней на единицу измерения, можно выразить формулой

Преобразуя это уравнение, получаем рабочую формулу прямолинейной регрессии. Обозначаем Ry/x через b:

Обозначаем = а, следовательно

В этом уравнении х является аргументом, у — его функцией. Уравнение показывает взаимоотношение между аргументом и функцией, именно то взаимоотношение признаков, которое и образует коэффициент регрессии. По этой формуле, зная значения аргумента (х) можно определить значение его функции (у) без непосредственного ее измерения.

В рассмотренном выше примере были вычислены коэффициенты корреляции и регрессии между уровнем яйценоскости и массой яиц у кур. Если принять яйценоскость кур за аргумент, можно составить следующее уравнение прямолинейной регрессии:

;

а = 56,6,127) ´ 102 = 56,68 + 12,95 – 69,63; а = 69,63

у = 69,63 + (-0,127) ´ x = 69,63 – 0,127 ´ x

Таким образом, для того, чтобы установить, какая масса яйца может соответствовать тому или иному уровню яйценоскости, нужно умножить показатель яйценоскости на коэффициент 0,127 и вычесть это произведение из числа 69,63. На основе этого уравнения можно заранее рассчитать значение функций для каждого значения аргумента. Таким образом, в частности в данном примере, можно составить ряд, показывающий регрессионные зависимости яйценоскости и массы яиц в данной популяции кур.

Теоретический ряд регрессии между признаками яйценоскости кур